将斯特恩—盖拉赫实验引入大学物理教学
汪亚平 宁长春 次仁尼玛 刘当波
(1西藏大学理学院实验中心,西藏 拉萨 850000;2西藏大学理学院物理系,西藏 拉萨 850000;3上海交通大学物理与天文学院,上海 200240)
斯特恩-盖拉赫实验,简单地说:就是让银原子通过非均匀磁场,观察其磁矩在非均匀磁场中的受力和偏转情况。该实验所包含的物理概念有:原子的结构(卢瑟福的原子核式模型、玻尔氢原子模型、玻尔-索末菲理论)、原子中价电子的轨道角动量、原子中价电子的轨道角动量磁矩、电子的自旋、电子的自旋磁矩、原子的总磁矩、磁矩在非均匀磁场中的受力分析、薛定谔方程、不确定性关系、波粒二象性等。
斯特恩-盖拉赫实验原本是属于原子物理、量子力学的教学内容。通行的各种大学物理教材中,都不会讲述这个实验。我们尝试按照时间顺序,从1916年索末菲提出“空间量子化”的概念(实验的最初动机),1922年“斯特恩-盖拉赫实验”得出实验结果(正确的实验给出了错误的解释),1927年“电子自旋”概念提出(实验的最终解释),一一展开其中的物理概念的教学。让学生体会到经典理论走向半经典半量子的旧量子理论,再了解量子力学的物理思想变化。让学习大学物理的非物理专业学生对该实验有一比较全面的了解。
1 载流线圈的磁矩以及载流线圈在磁场中的受力和运动
1.1 载流线圈磁矩的概念
对于一个载流线圈,将:
m=IS=ISen
(1)
定义为它的磁矩。其中,I是线圈中的电流强度;S是载流线圈包围的面积;en是载流线圈平面的法线单位矢量,规定其方向与线圈中电流的环绕方向满足右手螺旋定则。图1给出了一种最简单的载流线圈,亦即平面圆形载流线圈的磁矩。

图1 闭合回路具有的磁矩
1.2 载流线圈在均匀磁场中的受力和运动
将上述的载流线圈放在均匀磁场当中,其所受力矩为
M=m×B
(2)


图2 载流线圈放入均匀磁场
1.3 载流线圈在非均匀磁场中的受力和运动


图3 载流线圈放入不均匀磁场
1.4 无限小的载流线圈在非均匀磁场中的运动轨迹
为了与之后的叙述衔接,我们假设:第一,我们所讨论的载流线圈,是无限小的载流线圈,尺寸在原子的尺度,并且质量忽略不计,不受重力影响;第二,进入磁场的无限小的载流线圈,只具有上下两种磁矩方向。如图4所示,无限小且不受重力影响只具有上下两种磁矩方向的载流线圈,从S2处进入非均匀磁场,磁场的宽度为d,D表示载流线圈受到磁场力开始偏转到屏P的距离。z1是无限小载流线圈在磁场的出口处,偏离中轴线的垂直距离,z2是无限小载流线圈在P处偏离中轴线的垂直距离。

图4 无限小载流线圈在非均匀磁场中的运动轨迹
非均匀磁场的设置,让磁场梯度的方向沿着z轴,在x和y方向均为零。亦即:
(3)
所以无限小载流线圈受力只在z方向:
(4)

无限小载流线圈以速度v进入磁场区域,垂直方向受到力Fz的作用,做抛物线运动,运动方程是:
(5)
无限小载流线圈在经过磁场区(长度为d)时,已经偏离x轴z1距离。此时与x轴的偏角是
(6)
出了磁场,无限小载流线圈将沿直线运动,一直落在屏幕上面,偏离x轴的距离为
(7)
根据前述假设,进入磁场的无限小载流线圈的磁矩方向只能取上下两种,也就是cosθ=±1,所以按运动学的分析,可知无限小的载流线圈在经过磁场后,磁矩方向向上的,将会落在屏P的上方,磁矩方向向下的,将会落在屏P的下方。
2 氢原子的磁矩以及氢原子在磁场中的受力和运动
2.1 玻尔氢原子模型
如果研究的是一个带电粒子沿闭合回路运动(或者自旋),也可以按照式(1)来计算它所具有的磁矩,用式(2)来计算其在磁场中所受的磁力矩,以及用式(4)来计算它在非均匀磁场中的受力。这样,就可以将先前对于载流线圈的分析方法,用来分析氢原子。氢原子中的价电子围绕原子核(1个质子)做圆周运动。而这个价电子的闭合圆周运动,恰恰构成了一个闭合回路。下面讨论“将载流线圈放入非均匀磁场”转化为“将氢原子放入非均匀磁场”的情况。
玻尔氢原子模型中,有3个重要的假设。其一,定态假设;其二,跃迁假设;其三,轨道角动量量子化假设。其中轨道角动量量子化假设,实际上是将量子化条件从能量的数值扩展到轨道角动量的数值。玻尔明确指出:

(8)
2.2 氢原子的电子轨道角动量和电子的轨道磁矩的关系
下面给出氢原子的轨道角动量与其磁矩之间的关系。需要说明的是:在大学物理教材中,载流线圈的磁矩是用m表示,但是通行的教材里,原子的磁矩均是用μ表示。下文将用μ来表示原子的磁矩。

图5 电子的轨道角动量和磁矩的关系
如图5所示,如果原子中电子绕原子核旋转的频率是ν,轨道半径为r,则磁矩为
(9)

μ=-γL
(10)

(11)
式中μB为玻尔磁子。
由以上讨论可知,按照玻尔模型,氢原子中的价电子将沿闭合轨道运动,从而具有一个角动量,而这个角动量将会产生一个磁矩。于是,对于无限小的载流线圈的在磁场中的运动分析,可用于氢原子在非均匀磁场中的运动。
2.3 玻尔-索末菲理论
1916年,索末菲和德拜各自独立地对氢原子模型进行了修正,形成了“玻尔-索末菲理论”。亦即将玻尔氢原子模型的圆形轨道推广到椭圆形轨道,并且相应地,将玻尔原先的量子化条件从1个扩展到3个。
玻尔原先对于他的圆轨道提出的量子化条件中的n(n=1,2,3,…),被保留下来,后来被称为主量子数。另外又引入了两个新的量子数,一个是l(l=1,2,…,n),l和n一起,决定了椭圆形轨道的大小和形状(l=n时,椭圆轨道成为圆轨道)。一个是m(m的取值范围从-l到+l,不能等于零),被称为投影量子数(projection quantum number)。假如n=1,轨道是圆形轨道,索末菲和德拜的理论指出,这时m只能取+1或者-1,亦即轨道角动量在空间上只能取两个特定的方向。这个结论是惊人的!亦即索末菲和德拜在玻尔氢原子模型中角动量数值量子化条件和一个平面内轨道不连续之外,又加了一个空间取向上的量子化。这也就是当时所谓的空间量子化。
索末菲同时指出:在他的模型里,如果忽略相对论效应以及没有外加电场和外加磁场的前提下,能量取决于主量子数n,与l和m无关。但是如果考虑到相对论效应,l将对能量有微小的影响。而这种理论,居然恰恰能够很好地解释氢原子光谱的精细结构。
但是问题依然存在:既然氢原子中电子的能量和m无关,也就是说氢原子光谱和m无关,在不加外加电磁场的情况下,我们就无法感知到空间量子化的存在。索末菲的观点是:m所决定的离散的空间取向,在空间上是等价的,如果在空间当中没有一个相应的选定的参考方向,就无法感知。但是如果一个外加的电场或者磁场,来给予这样一个参考方向,不同的空间方向将会在能量上显示出差异。(电子的运动路径的法线方向与外加磁场的方向之间的夹角,决定电子与磁场之间的相互作用。)图6给出了玻尔氢原子模型与玻尔-索末菲氢原子模型的差别。

图6 索末菲对于玻尔理论进行的修正

图7 氢原子在非均匀磁场中的受力
2.4 氢原子在磁场中的受力分析

(12)
其中,θ指的是氢原子的磁矩方向与磁场方向的夹角。
注意式(12)来自于式(4),只是为遵从原子物理以及量子物理中的习惯,用μ这个符号来表示氢原子的磁矩。
需要注意的是:载流线圈磁矩的空间取向,可以取任意一个方向,亦即是连续的。这就意味着:cosθ可以在-1和+1之间取任意值。那么一个载流线圈进入非均匀磁场之后,可以朝向任意方向运动。但在玻尔-索末菲理论中,氢原子的角动量,空间取向却是量子化的,亦即意味着氢原子的磁矩取向也是量子化的,进入外加磁场的氢原子的磁矩方向,只能取“上”或者“下”两个方向。亦即在非均匀磁场中,磁矩向上的氢原子只能往上运动,磁矩向下的氢原子只能往下运动。
3 斯特恩-盖拉赫实验以及对之的几种解释
下面介绍斯特恩-盖拉赫实验的实验装置和实验原理。
3.1 实验装置

图8 斯特恩-盖拉赫实验装置
实验装置如图8所示。第一,这个实验装置中,采用的不是氢原子,而是银原子。银原子从炉子内被蒸发出来,要经过狭缝状的两个准直器,进入非均匀磁场。第二,非均匀磁场是由两块特殊形状的磁铁构成(如图所示,磁场梯度沿z轴正向)。第三、银原子经过非均匀磁场之后,继续前进,会打在一块冷却的玻璃板上,银原子将沉积在玻璃板上,形成一定的沉淀形状。
假设在理论上,银原子和氢原子在磁场中表现一模一样,那么氢原子究竟是否存在空间量子化的问题,恰如斯特恩所说:只要观察玻璃板上的沉积形状即可。
3.2 经典理论对于实验结果的预期
基于上述基本物理概念很容易理解经典理论对于这个实验结果的预期。如果进入磁场后,氢原子价电子的轨道角动量取向任意,磁矩取向自然也是任意方向。让氢原子进入斯特恩-盖拉赫实验装置,外加磁场的方向在z轴上,磁场梯度的方向在z轴正方向上,那么氢原子磁矩μ的取向任意,如图9所示,使得磁矩和z轴的夹角可以取任意数值,则cosθ的取值自然可以从-1到+1之间取任意值,于是磁矩在z轴方向上的投影μz=μcosθ可以取任意值。

图9 经典理论对于实验结果的预期
进入磁场的氢原子的价电子的磁矩,具有随机的空间取向,μz=μcosθ的数值将会大小不同,数值连续分布,按照式(12),每一个氢原子所受的向上或者向下的力,也应该大小不同,但在数值上是连续分布。就大量的氢原子而言,向上运动和向下运动,从而与y轴(中轴线)偏离的角度也应该连续取值,并且总数量在任意一个角度上平权。这样偏转并在前进一段距离之后,最后打在玻璃板上,只是原先的分子束形(狭缝)被在z轴上展宽而已。飞行距离越远,分子速度越小,展宽越厉害。所以经典理论对于这个实验结果的预期是:将会在玻璃板上出现被展宽的连续分布的分子束形。
3.3 旧量子理论对于实验结果的预期
按照玻尔-索末菲理论,因为进入磁场的氢原子天然地感知到了磁场的方向,于是其价电子的轨道角动量只能取上下两种方向,式(12)当中的cosθ只能取+1或者-1,于是氢原子在z方向上,也只能感受到上下两种方向的力。于是,一切分析变得和1.4节中的叙述一致。也就是说,在氢原子经过非均匀磁场,然后继续飞行,抵达P(玻璃板,见图10)时,按照式(7),z2只能有两个取值。(实际上这时,我们会感受到玻尔-索末菲理论在n和l之外,提出m的惊人之处。因为如果没有这个m,即便n和l是量子化的,也只能导致角动量数值上的量子化,因为cosθ依然可以取连续值,从而导致μz=μcosθ依然可以取连续值,从而影响到z2也会取连续的值,而不会出现量子化的结果。也就是说:只有当μ在z方向的投影是量子化的,z2的数值才可能是分立的。z2的数值分立,反过来可以证明μz是否量子化。)

斯特恩认为这个实验结果的确是验证了空间量子化的概念。因为按照玻尔-索末菲理论,如图11所示,预设一个方向(通过外加磁场实现),相对于这个方向,氢原子的角动量只能有两个方向,亦即磁矩只能有上下两个方向。这样,氢原子在磁场中,只能有1/2的氢原子向上运动,1/2的氢原子向下运动。于是玻璃板上只能出现一个分裂的分子束形。

图10 旧量子论对实验结果的预期

图11 旧量子论对于氢原子磁矩的判断
3.4 量子力学对于实验结果的解释
实际上,1922年的实验结果出来之后,斯特恩的确认为这个实验验证了空间量子化的概念。但是现在我们知道,这个正确的实验,验证了一个错误的理论。因为对于这个实验正确的解释,要根据量子力学来处理。为了完成这个事情,我们按照杨福家教材里的叙述方法,给出量子力学对于这个实验结果的一个大体解释。之后将介绍大学物理通行教材中量子力学的基本知识,再用这些量子力学的基本概念,对该实验结果给出更为详尽的量子力学解释。
3.4.1 量子力学对于实验结果的大体解释

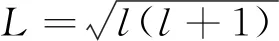
(13)
而式(13)是由量子力学的计算得到的(氢原子的薛定谔方程的解.说明不仅轨道角动量的z分量Lz是量子化的,L本身也是量子化的。l称为角动量量子数。)
于是,在量子力学中,将式(13)代入式(10),氢原子磁矩大小的表达式为

(14)
(用μl,原因是认为氢原子的磁矩全部是由价电子的轨道角动量贡献的)再次用到氢原子薛定谔方程的一个求解结果:
Lz=m,m=0,±1,±2,…,±l
(15)
(此式表示的是角动量在z方向上的投影大小。形式上与玻尔氢原子模型中的角动量量子化条件一样,但是,这个公式出现在这里,却是求解薛定谔方程得到的,m称为磁量子数。)
下面,将式(15)用到式(14)中,便得到磁矩在z方向上的投影:
(16)
(为了区分电子的质量和式(15)中的磁量子数,此处用ml表示磁量子数)。这样又有:
式(17)、式(18)两式,表明氢原子的磁矩及其z分量的大小是量子化的,来源于电子的轨道角动量L及z分量Lz的大小的量子化。而Lz的量子化表明了角动量在空间取向的量子化。即角动量量子数为l时,角动量在空间有2l+1个取向,它对应有2l+1个投影值ml。
到此,问题是:斯特恩-盖拉赫实验尽管证明了原子在磁场中的空间量子化,但是却不能解释氢原子在磁场中只有两个取向的事实。空间量子化认为,l一定,ml=2l+1.也即是说:l是整数,2l+1一定是奇数。这说明我们对原子的描述仍然是不完备的。
实际上,这个实验结果出现偶数分裂,说明要2l+1为偶数,只有角动量为半整数才可以。轨道角动量不可能出现半整数。乌伦贝克1925年提出:电子不是点电荷,除了轨道角动量,还有自旋运动,固有的自旋角动量为S:

(19)

Sz=ms,
(20)
有了这个假设之后,便有了与自旋相联系的磁矩:
(21)
由于这两个式子与实验事实不符,再次假设电子的磁矩为1个玻尔磁子,也就是经典数值的2倍。磁矩的方向与自选的方向相反。(这个假设,与电子自旋概念一起,可以由狄拉克相对论量子力学严格导出)这意味着,式(17)、式(18)两式,在原子体系中并不严格成立。于是定义一个g因子,使得对任意角动量j所对应的磁矩,以及在z方向的投影,可以表示为
只考虑到轨道角动量时,j=l,则gl=1
重新回到式(17)、式(18)。这是借助于经典的轨道概念再加上量子化条件得到的。
只考虑电子的自旋时,j=s,则gs=2。到此为止,g只是一个假设。称为朗德因子。
(以上,将小写的j,l,s分别表示电子的总角动量,轨道角动量,自旋角动量。目的是区分多电子原子所用的角动量的符号。)
电子的总磁矩,在引入电子自旋磁矩的概念后,可以用图12计算。(暂不考虑原子核的贡献,原子核的质量,比电子的质量大3个数量级,磁矩是与质量成反比。那么原子核的磁矩要比电子的磁矩小3个数量级。原子核磁矩对于原子的贡献,在于超精细相互作用。)

图12 电子磁矩与角动量的关系

从图12中可以看出,μ不是一个具有确定方向的量,可分解为两个量。一个沿着j的沿线,叫做μj,这是有一定方向的恒量。另一个垂直于j,由于绕着j转动,对外平均效果抵消了。因此,对外发生作用的是μj,即电子的总磁矩。

如果将电子的自旋也考虑进去,实验结果的解释应该是(如果不考虑电子的自旋,无法解释偶数分裂):原子的磁矩应该用式(23)。于是式(7)变成:
(24)
由于mJ=J,J-1,…,-J,共有2J+1个数值。相应有2J+1个分立的z2数值。那么具体到处于基态的氢原子:

3.4.2 大学物理中的量子力学基本概念
1) 薛定谔方程
给出薛定谔方程
i
(25)
其中,Ψ=Ψ(x,y,z,t)叫做波函数。其一维形式是:
i
(26)
大学物理中的知识,至少可以让同学明白,在量子力学中上述方程就相当于经典力学中的牛顿第二定律。对保守体系,力可以表示成势能函数的导数,F=-∂V/∂x,V表示的就是势能函数。
以一维波函数为例,略去求解的过程,可以直接写出方程的解为
(27)
之前用到的式(13),就是氢原子薛定谔方程的解。而式(22)和式(23),是由狄拉克相对论量子力学导出。
2) 电子自旋

量子力学中,电子自旋会赋予电子一个内禀自旋磁矩:
(28)
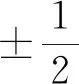
另外,在量子力学中,薛定谔方程和海森堡的矩阵力学是等价的。也就是说,薛定谔方程中的算符也可以用矩阵算符来代替。而对于电子自旋这样的双能级系统而言,这无疑是更方便的处理方式。令式(27)当中的N=2,我们可以用矩阵的算符去描述电子的自旋体系:
(29)
其中,
(30)
(31)
则σz的本征态可以表示成:
(32)
于是↑和↓就分别表示z方向上的上和下。利用式(27),可以写出电子自旋的波函数:
(33)
E↑和E↓分别代表H的本征值,对应着ψ↑和ψ↓。
3.4.3 量子力学对于实验结果的严格解释框架
根据以上知识,对于斯特恩-盖拉赫实验进行解释。
首先,这个实验当中,哈密顿算符是:
(34)
利用式(28)、式(29)、式(30),也可以写成:
(35)
设氢原子进入磁场的时间为T,有:
(36)
由此可以得出:
(37)
再次用式(33),有:
(38)
上式即离开磁场后的原子的状态(t≥T)。
将这式与下式比较:
(39)
我们可以得出:
(40)
其中,±意味着电子自旋的两个指向在z方向采取了上和下两种状态。注意其与磁场梯度b正比。也就是说,如果电子自旋取向随机,进入我们设计的磁场,将会在离开磁场的时候,只具有上下两种自旋方式,因为自旋的表现χ↑↓与±pz纠缠在一起。由此,斯特恩-盖拉赫实验从量子力学得到严格解释。
4 将斯特恩-盖拉赫实验引入大学物理的主要困难
文章的源头,是从一个无限小的载流线圈讲起,之后,在用无限小的载流线圈来比拟银原子的磁矩,到此时,才觉得为了形象地让同学理解这个实验,导致了另外的一些风险。这风险就在于试图用经典物理的思维方式,去理解与经典物理完全不同的量子力学的物理概念。有必要将这个风险告知学生。
第一,这个实验的解释,在本质上,根本与经典物理的概念不沾边(归因于经典物理和量子力学完全是两种知识体系)。也即是说:这个实验只能用量子力学的基本原理去说明。当然这也意味着为了让学生真正的洞察斯特恩-盖拉赫实验的物理本质,离不开量子力学所需要的基本的物理概念和数学工具。第二,因为认知的需要,原子物理教材当中叙述这个实验,也有用到半经典半量子的叙述方式去讲述这个实验,所以从电子轨道的概念引出电子的轨道角动量,进而引出电子磁矩的概念等做法,一直沿用至今。实际上需要给同学讲清楚,这种做法仅仅是为了促进认知和理解,实际上已经偏离了物理本质。费曼说:我们必须用一种抽象的或想象的方式,而不是把它与我们的直接经验联系起来的方式去学习量子力学。本文另外一个期望,就是在让学生明白这个事实的前提下,以大学物理教学内容中的基本物理概念为基础,尽可能走进氢原子的内部,更深入地理解斯特恩-盖拉赫实验,以及以理解这个实验为手段,了解量子力学的一些基本原理,以引发学生学习量子力学的兴趣。
还需要交代清楚叠加态和混合态的问题。假设送入斯特恩-盖拉赫实验装置的是许多个角动量只有上下两种取向的无限小载流线圈,这与送入斯特恩-盖拉赫实验装置的许多个银原子,本质的区别在于:许多个角动量只有上下两种取向的无限小载流线圈,每一个载流线圈在送入实验装置之前,其实都有确定的磁矩方向(要么上,要么下),但是由于其总体数量巨大,在空间上下两个方向上均有50%的分布,在进入非均匀磁场之后,亦会出现上下分裂的两束。但是许多个银原子,与无限小的载流线圈的区别在于,在测量之前,每一个银原子的价电子的自旋,并不确定。只是向上自旋和向下自旋这两种态的叠加。而是测量本身,使得银原子分裂为上下两束,亦即使得银原子价电子自旋上下两种状态得到了明确的确定。
5 结论
本文紧扣大学物理的基本物理概念,从一个小的载流线圈所具有的磁矩讲起,将之放入非均匀磁场,探讨其受力和运动。之后引入玻尔-索末菲模型,让氢原子价电子的轨道角动量和磁矩建立联系,引入轨道角动量量子化的概念(角动量数值的量子化、轨道大小的量子化、轨道角动量空间取向的量子化),从半经典半量子的方式,说明角动量量子化会导致磁矩量子化,氢原子将如同一个无限小的载流线圈一样(只不过空间取向量子化),在磁场中产生离散的偏转。然后提出斯特恩-盖拉赫实验的实验背景和实验原理,在此基础上,进一步讲解经典物理对于斯特恩-盖拉赫实验结果的预期、旧的量子力学对实验结果的解释,以及量子力学对于实验结果的最终解释。在这之后,以解释斯特恩-盖拉赫实验为导向,简单梳理了大学物理教学内容中量子力学的基本知识点并稍有拓展(主要是电子自旋)。并且指出量子力学和经典力学是完全不同的两种知识体系,这种将无限小的载流线圈和氢原子的磁矩(实际上是与电子自旋)相比拟的讲解方法,纯属形象化的教学所需,着重强调了叠加态和混合态的区别。文章结尾,对于将斯特恩-盖拉赫实验引入大学物理存在的困难进行了简要的提及,以供有兴趣的老师进行进一步的追究。

