径向摆的运动状态及其混沌状态的研究

陈宗强 王 远 余 华

(南开大学物理科学学院，天津 300071)

在2018年国际青年物理学家锦标赛(IYPT)题目中径向摆(Azimuthal-Radial Pendulum)的题目内容为：“Fix one end of a horizontal elastic rod to a rigid stand. Support the other end of the rod with a taut string to avoid vertical deflection and suspend a bob from it on another string (see figure1). In the resulting pendulum the radial oscillations (parallel to the rod) can spontaneously convert into azimuthal oscillations (perpendicular to the rod) and vice versa. Investigate the phenomenon.”翻译为：“将水平弹性杆的一端固定在刚性支架上。用一根绷紧的绳子支撑杆的另一端，以避免垂直偏转，并将它从另一根弦上悬挂下来(图1)。在摆动中，径向振荡(平行于杆)可以自发地转变为方位振荡(垂直于杆)，反之亦然。研究这种现象。”

图1 径向摆的示意图

复摆一直以来是人们感兴趣研究对象之一，孙为民等人对拉扭耦合振子特性进行研究[5]；许裕栗等人对韦氏耦合摆共振机理给出了解释[5]；Eugene等对受迫共振的对摆的运动发生变化进行了研究[5]；龚善初等对复摆运动体系的Lyapunov指数进行了研究[5]；郑子辰等人给出的无耗散耦合摆动力学方程[5]；Vittorio Picciarelli等人从最简单的模式分析，并给出耦合振子方程[5]。本文运用分析力学进行研究，解释了径向摆的运动轨迹转变的物理原因，并由受迫共振给出了摆的运动发生几种不同转变的原因与条件，分析了复摆体系运动的Lyapunov指数,并给出了混沌现象产生的条件。

1 模型建立

径向摆产生这种轨迹的原因是弹性杆能发生形变，下面将在杆形变是影响摆球运动的基础上进行分析。

图2 模型的建立建立两个坐标系，随动坐标系(x0，y0，z0)是建立在摆绳连接点处的笛卡尔坐标系，它随连接点平动但本身不发生转动。静止参考系(x，y，z)是建立在弹性杆连接点处的笛卡尔坐标系。图中用圆圈标出的两个坐标参量以及圆圈标出的角度参量(x，y，θ，α)对应我们选取的4个自由度，其中，θ为水平面上x轴与弯曲弹性杆末端切线方向的夹角；α为摆绳与z轴方向的夹角；ψ为悬挂绳与弯曲弹性杆末端切线方向的夹角

由于弹性杆受到悬线的限制，弹性杆在竖直方向上的运动被约束，于是规定直角坐标系(x0,y0,z0)是建立在摆绳连接点的随动(相对于连接点)参考系, 而(x,y,z)为建立在弹性杆固连点上的静止参考系，如图2所示。在弹性杆的竖直自由度被限制以及刚性绳不可伸长的条件下，径向摆体系将是一个四自由度体系，(x,y,θ,α)为4个自由度的代表坐标。其中，θ为水平面上x轴与弯曲弹性杆末端切线方向的夹角；α为摆绳与z轴方向的夹角；ψ为悬挂绳与弯曲弹性杆末端切线方向的夹角。

弹性杆所发生的形变在两个方向，径向与切向。它们体现在受摆球作用力影响下摆悬挂点位置相对于弹性杆不受挠矩时悬挂点的位移，分别对应剪切应变与径向张应变。根据弹性理论[7]，利用边界条件、相容性条件以及应力方程可以导得此时弹性杆的形变方程以及对应的能量方程。约定符号：记ξx为径向位移，ξy为切向位移，Y为杨氏模量，S为弹性杆截面积，ρ为弹性杆的密度，I为弹性杆的惯量积，l为有效长度(摆连接点到弹性杆固定点的距离)，Δl为附加长度(摆连接点到弹性杆端点的距离)。

对于弹性杆的张应变能量[7](势能与动能)，其弹性杆张应变的动能为

(1)

其弹性杆张应变的势能为

(2)

对于弹性杆发生切应变所对应的能量，亦可得到为

其中，动能项中的系数5/2268比较复杂，这是由于在分析时并不能完全使用准静态模型，还应考虑挠矩与切应变的相位差导致的[7]。

由此，在此处我们采用切应变动力学分析后得到了上述结果，其分析过程在古登堡的弹性体力学中已有充分论述，此处不再做解释。

对于阻力，复摆体系中主要来源有两种，一种是空气阻力，另一种是由于杆和摆之间摩擦耗散。

实验中，摆球运动速度全程处于低马赫状态，其受的空气阻力将正比于物体运动速度大小，而由耗散引起的摆的振幅衰减，一般是线性衰减，其衰减因子(某一时刻振幅与初态振幅之比)，可以写成指数形式：

κ(t)=e-γt

(5)

式中，γ为衰减常数。

给出体系的拉格朗日方程中的动能与势能形式，对于体系动能：

(6)

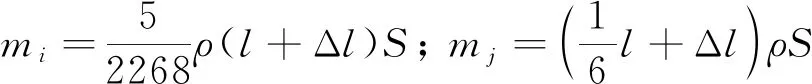
(7)

广义坐标qi的选择：在这个方位角—径向摆的四自由度体系中，选取的广义坐标正是之前建立坐标系时选取代表4个自由度的坐标(x,y,θ,α)。

2 受迫振动与摆的运动方向

通过对弹性杆受迫振动的分析，可以给出径向摆体系中摆运动发生转换与稳定的条件。弹性杆自身的振动存在着对应本征频率。

由无外力驱动时弹性杆的自发振动方程(假设弹性杆受到了微扰开始振动)：

(8)

由此，可以得到弹性杆在x和y两个方向振动固有频率：

当弹性杆在某方向振动时的固有频率和摆本身的固有频率更为接近时，平衡位置将偏向此方向。

3 实验装置

利用实验室弹性杆、铁架台、机械臂、支架螺钮搭建简易的实验装置如图3所示。

图3 方位角—径向摆的实验装置

我们用杨氏模量测量仪测出弹性杆的杨氏模量，用直尺测量摆线的长度，用游标卡尺测量有效长度的变化以及摆球的直径，用天枰测出摆球的质量。

其各个参数如下所示：

Y=30.34×106N/m2，

ρ=1218kg/m3，d=20.0mm，

l0=21.0cm，m=32.16g，

I=2.48×10-9m4，g=9.8m/s2，

Δl=2.0cm。

实验中，我们首先观察到两种现象：

(1) 由阻力引起的摆的振幅衰减；

(2) 弹性杆的两种形变以及对应产生的摆球运动轨迹的变化。

采用较小的有效长度l=0.06m。发现此时振动在x方向(径向)附近稳定，此时从其他方向上(不同于x轴的方向)释放的摆球摆动轨迹将向x方向旋转，并且稳定在x轴附近；而从x轴附近释放的摆球摆动轨迹是稳定的(不会发生旋转)，如图4(a)、图4(c)所示。

采用较长的有效长度l=0.28m，振动在y方向(切向)附近稳定，此时从其他方向(不同于y轴的方向)上释放的摆球摆动轨迹将向y方向旋转，并且稳定在y轴附近；而从y轴附近释放的摆球摆动轨迹是稳定的(不会发生旋转)，如图4(b)、图4(d)所示。

当采用有效长度为l=0.1065m的弹性棒进行实验，观察到在径向与切向的两个方向上耦合强度接近，可以判断此时从径向和切向上释放的摆的轨迹都不会发生转动。如图4(e)、图4(f)所示。

以弹性杆直径和体系的附加长度为例：图5(a)改变弹性杆直径与体系的有效长度来绘制相图，图5(b)改变体系的有效长度和附加长度来进行相图绘制。可以通过划分区域的方式定义方位角—径向摆体系的不同稳定方向，在两个相图中我们还找到了一条稳定线，在稳定线附近释放的摆同时在切向和径向达到稳定。

图5 平衡位置的相图

4 运动模式的模拟

采用较小有效长度l=0.06m，此时弹性摆的平衡位置将在方向x附近，若计算此时几个本征频率间的关系，其中ω0为摆在竖直平面内振动的本征频率。

ωx-ω0=3899.6rad/s

ωy-ω0=5935.9rad/s

(9)

其次，采用较大的有效长度l=0.28m，进行实验，发现弹性摆的位置确实将在y附近：

ωx-ω0=904.5rad/s

ωy-ω0=316.6rad/s

(10)

对于之前在实验中观察到了特殊的稳定现象，即在两个方向释放得摆的运动都是稳定的，对于长度为l=0.1065m的弹性棒：

ωx-ω0=2560.7rad/s

ω0-ωy=2560.7rad/s

(11)

我们发现在这样的条件下固有频率在两个方向的耦合程度是接近的，同时存在两个方向的稳态，前两种情况具体的理论模拟图如图6所示。

图6 径向摆的运动模式模拟图

对于本征频率，杆的振动本征频率远大于摆球本身的振动本征频率。杆在两个方向上振动的本征频率与摆球振动频率的差在同一量级上。在共振效应的影响下，这个差值越小相对应的振幅将会越大。

5 非线性与混沌

在实验中，除了前几种现象之外，我们还观测到在某些条件下摆的运动具有很大的无序性。对于这类运动出现的原因是由于弹性杆与摆球的运动耦合时本身存在着非线性项，当弹性杆的杨氏模量与半径较小时，非线性效应明显，而使弹性杆振动的非线性效应与摆球运动的非线性效应发生耦合。

利用傅里叶分析，分析这类运动的能量频带如图7所示。可发现：能量频率关系并不是只有几个峰值而是一个连续波动的函数，这正是由于非线性成分的耦合引起的。

图7 运动非线性运动的傅里叶分解图

利用Wolf法，分析上述条件下的弹性棒运动的Lyapunov指数。调整弹性杆的半径，初态的Lyapunov指数是小于零的。随着模拟，可以发现随着杆的杨氏模量减小，Lyapunov指数逐渐上升，见表1。

表1 弹性杆半径与Lyapunov指数

当体系的Lyapunov指数大于零时，体系将会产生混沌现象，由此可以得出混沌现象可能发生在弹性杆杨氏模量极小的极端情况。

6 总结

本文对第31届IYPT赛题中提到径向摆现象进行了研究。利用分析力学原理详细解释了径向摆中存在着摆球运动轨迹转动的原因，利用受迫共振与力矩，解释了摆球运动轨迹转变的方向与条件，并给出了实验检测以及与理论模拟进行对比。最后还研究了复摆体系存在的非线性现象，给出混沌可能发生的条件。结果如下：

(1)ω0(摆球振动的本征频率)接近ωx时，摆球轨迹将向x(径向)方向转化，最终稳定在x(径向)方向附近。

(2)ω0接近ωy时，摆球轨迹将向y(切向)方向转化，最终稳定在y(切向)方向附近。

(3)ω0与ωy和ωx耦合强度接近时，从径向和切向释放的摆球的运动轨迹都是稳定的，不会发生转动。

(4) 方位角—径向摆体系中存在着非线性的耦合现象，当弹性杆的杨氏模量极小时可能有混沌现象发生。