声速差计算方法及其在对外加非均匀应力评价中的应用

郭彦弘 ， 卢 超 ， 何方成 ， 梁 菁 ， 王 晓 ,*

（1.中国航发北京航空材料研究院 检测中心，北京 100095；2.无损检测技术教育部重点实验室（南昌航空大学），南昌 330063）

0 引言

随着国家航空工业的快速发展，对飞机各个零部件的韧性、强度、抗应力性能和抗腐蚀性能等的要求越来越高。铝合金是航空工业中的重要结构材料，其具有密度小、强度高、塑性好等优点。但铝合金结构件在加工后经常会出现弯曲、扭曲、弯扭组合等变形，使零件难以达到设计要求。研究发现，产生上述情况的主要因素就是残余应力。铝合金零部件的尺寸精度会因为材料内部应力状况的改变而受到影响，降低铝合金结构件的各项指标，最终影响到机器性能。因此，对残余应力的深入研究具有非常重大的意义[1-2]。

测量残余应力在国内外都是一个难题。测量残余应力的方法一般分为有损方法和无损方法。有损方法有钻孔法、轮廓法等，无损方法有X 射线衍射法、中子衍射法、超声法等。其中，超声法是一种经济适用的无损测量方法，它可以测量材料的表面应力以及内部应力。该方法因为要求不高、操作简便、测试设备相对简单，而成为工业应用型的一种应力测试方法[3-5]。

超声法测量残余应力的原理是基于声弹性理论，这一理论最早于1940 年提出的。美国学者根据有限变形理论，提出了各向同性材料声弹性理论的早期表达形式，建立了超声波在材料中传播时速度与应力之间的关系，由此奠定了超声波应力测量的基础。近年来，国内对残余应力的研究也逐渐增多。2008 年，赵翠华[6]基于临界值折射纵波建立了一套超声波残余应力测量系统，测量平板对焊的纵向残余应力并用其他方法进行验证；路浩等[7-8]基于临界折射纵波建立了超声波法焊接残余应力测量系统，测量了铝合金平板纵向残余应力场梯度，并指出声弹性的非线性原理的进一步发展是完成工程结构残余应力精确测量的基础；2009 年，马子奇[9]基于声弹性理论开发了一套应力测量系统，实现了在线检测薄壁焊接件应力；2012～2013 年，Javadi Y 等[10-12]利用临界折射纵波法，对不锈钢和碳钢管道焊接接头的周向与轴向残余应力进行了测量；2014 年，徐春广等[13]建立超声应力检测系统，对多种钢和铝合金进行超声与X 射线检测，对比结果显示二者应力趋势基本相同；2016 年，宋文涛[14]通过理论研究与仿真模拟，建立了应力检测与调控的系统，实现了残余应力检测与调控的闭环控制；2019 年，徐丽霞等[15]对航天铝合金平面双向应力进行超声检测研究，并对比其他检测方法，结果表明，超声法与钻孔法测量值近似相同，与X 射线法趋势基本相同。

本研究使用有限元软件仿真计算推导不同程度应变下铝合金试样的应力分布和声速极差，再通过对7050−T7451 铝合金试样施加与仿真同应变程度的外加应力，实测超声纵波声速分布验证仿真结果。

1 非均匀应力场中的声速理论计算

物体处于无应力、无应变的状态为状态I，质点的位置用矢量 ξ或其分量 ξα（ α=1,2,3）表示，ξα称为自然坐标。物体预变形状态为状态II，质点的位置矢量用 X 或其分量 XJ（ J=1,2,3） 表示， XJ称为初始坐标。在预变形的物体上叠加声波小扰动，使物体进一步变形到达最终状态（状态III），质点的位置矢量用 x 或 其分量 xj（ j=1,2,3）表示，变形物体坐标系如图1 所示。状态I、状态II 和状态III 之间的关系[16]为：

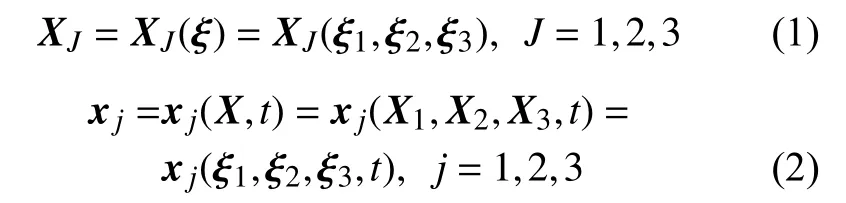
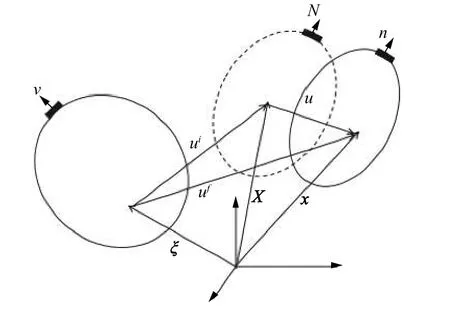
图 1 变形物体的坐标系Fig.1 Coordinate system of deformed object

从状态I 到状态III 的声弹性运动方程为：

其中，

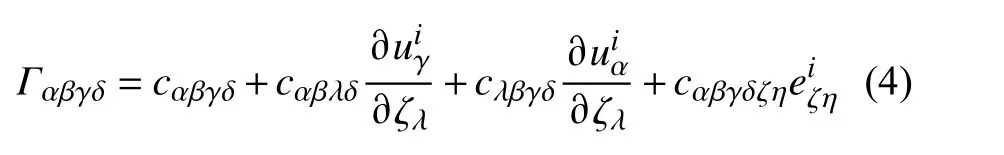
在均匀变形的情况下，通过声弹性运动方程的进一步研究，最终得到在均匀变形情况下的一组波速方程：

零应力状态下的纵波在介质中的传播声速为：

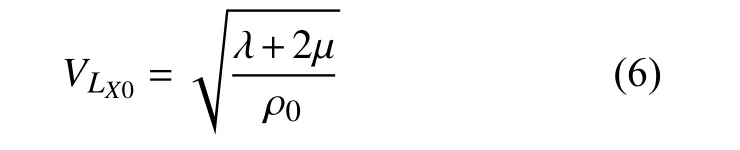
有无应力之间的关系为：

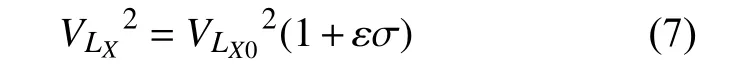
声弹性系数表示为：

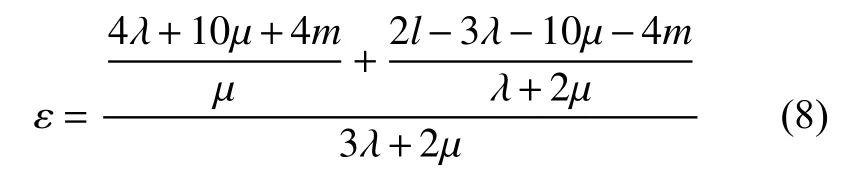
式中：V 为速度，下标X 为沿X 轴方向的轴向张力，即 VLX为沿应力方向传播的纵波声速； ρ0为状态I 下的材料密度；λ 和μ 为各向同性材料的二阶弹性常数；l、m、n 为各向同性材料的三阶弹性常数； σ为轴向张力； K0为各向同性材料在状态I 下的体积模量；ε 为声弹性系数。常用材料的Murnahan 常数和Lame 常数见表1。

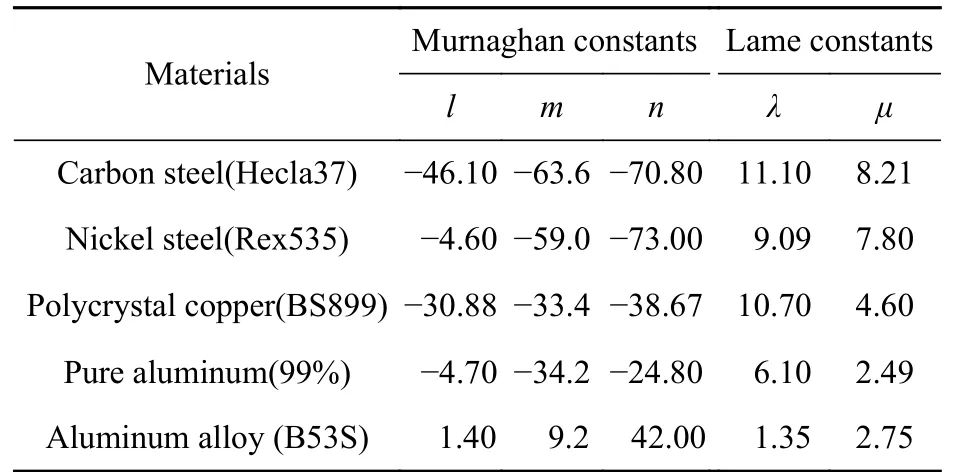
表 1 一些材料的Murnahan 常数和Lame 常数Table 1 Murnahan constant and Lame constant of some materials

根据王晓等[17]的超声测量非均匀应力场实验研究可知，在波速方程中若只受到单向应力作用，应力和声速的平方呈正比关系。但由于应力引起的声速变化较小，上述声弹性方程只需进行一次展开，后续的多项式作为余项，可忽略不计。已有的超声波传播时间与应力关系如图2 所示。

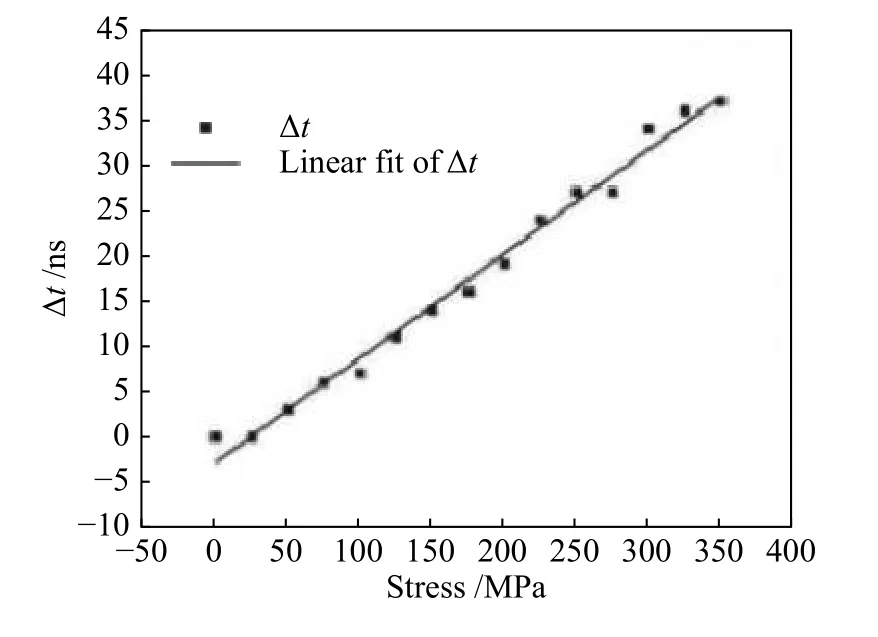
图 2 5 MHz 探头测得的标定试样中应力与传播时间变化关系Fig.2 Relationship between stress in calibration specimen and TOF tested by transducers with frequency of 5 MHZ

2 有限元仿真

利用Abaqus 进行铝合金试样有限元建模，如图3 所示，通过添加螺栓载荷与接触面约束，得到4 种不同的U 型缺口底端变形距离，提取其应力场进行计算。

Abaqus 有限元仿真下的不同形变的试样Mises 应力场如图4 所示（1#状态为未施加应力）。可以看到，有限元仿真获得的应力分布结果符合应力分布规律。提取不同应变条件下的应力场后通过观察可知，与正应力σ 相比，切应力 τ较小，可忽略不计，故σ11、σ22、σ33近似为3 个主应力σ1、σ2、σ3。σ2、σ3为主要应力分量，σ1较小，如图5 所示。

忽略切应力( τ12, τ13, τ23)分量的影响后，超声波的波速变化只受到3 个正应力的影响，可简写为：

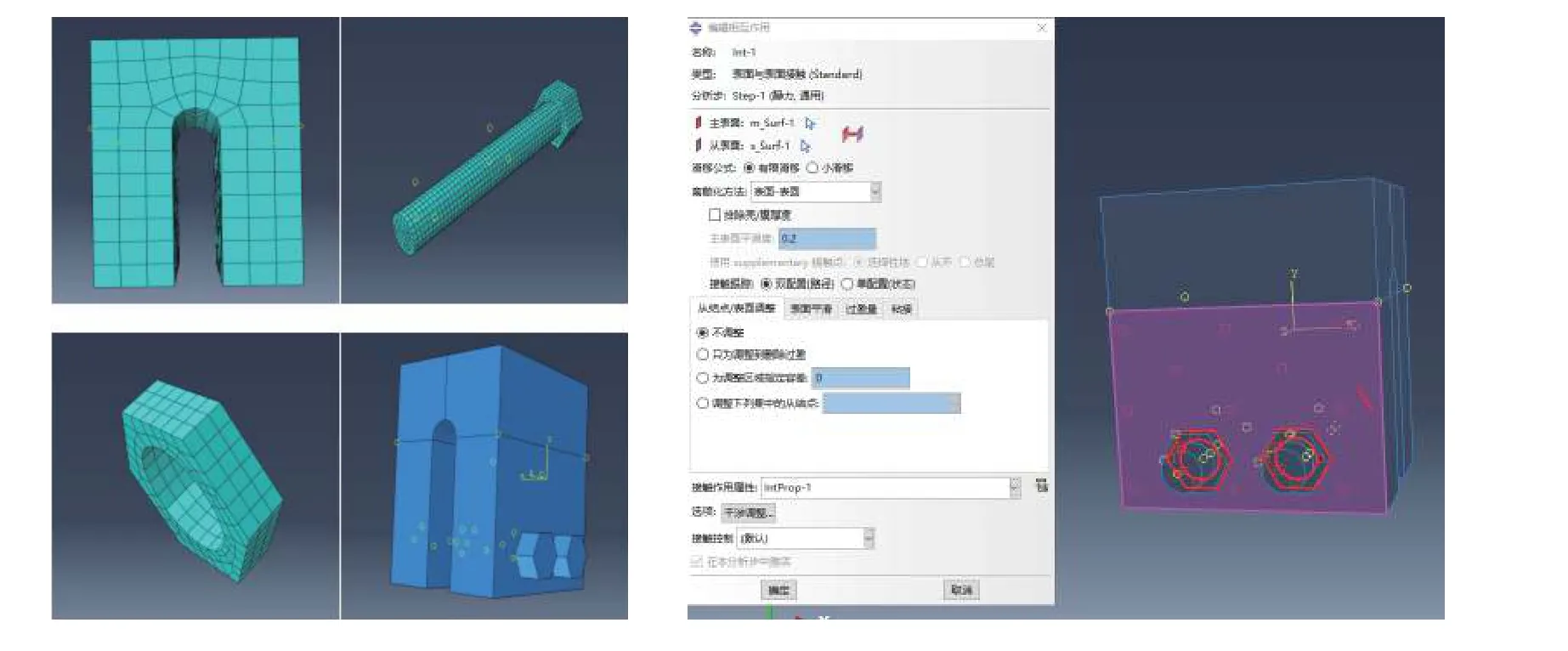
图 3 有限元建模Fig.3 Finite element modeling

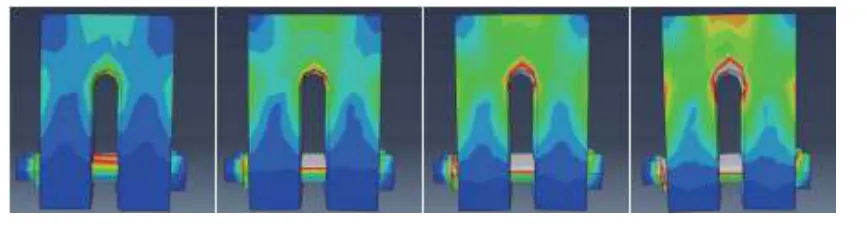
图 4 Mises 应力场Fig.4 Mises stress field

图 5 不同应变条件下的应力场Fig.5 Stress Field under different strain conditions

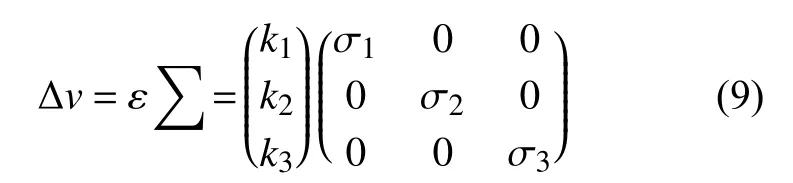
声速变化方程展开后纵波声速改变量方程式为：

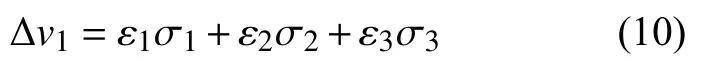
提取各应变状态下的最高应力处的全厚度方向应力场，根据公式（10），计算变形状态模型下的声速极差，结果如图6 所示，声速极差随变形量的增加而增大，二者呈非线性递增关系。

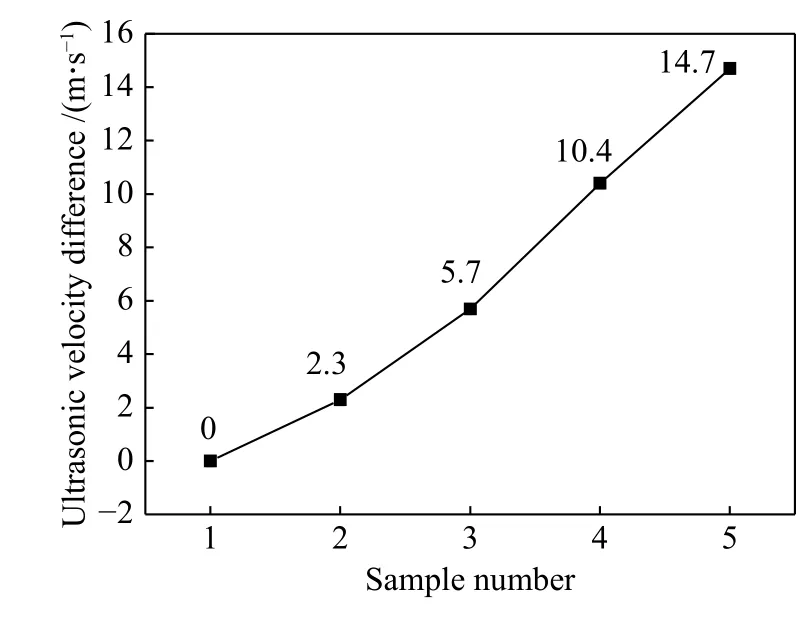
图 6 试样的声速极差Fig.6 Ultrasonic velocity difference of sample

3 试验测试

3.1 试样制备与试验方法

为了研究声速对非均匀应力的响应，利用螺栓对7050−T7451 铝合金试样进行加载，合金试样与仿真试样一致，实物及尺寸如图7 所示。

3.2 试验方法

采用5 MHz 水浸平探头，水距为30 mm，使超声波沿高度方向传播，并沿试样长度和宽度方向扫查，然后分次拧紧螺栓施加不同应力改变变形量达到仿真同等应变（表2），对不同变形程度试样分别进行扫查，获得超声速度分布图。

3.3 声速成像C 扫描结果

图 7 7050 铝合金试样Fig.7 7050 aluminium alloy sample

表 2 试样变形量Table 2 Sample deformation mm

图8 是铝合金超声C 扫描声速结果，声速数据色标在图右边表示，超声波声速结果以不同颜色进行表示，红区为声速高，蓝区声速低，声速极差为测量声速最高值减去最低值。超声法获得的应力分布与应力集中区结果符合应力分布规律，超声法表征结果与仿真表征结果具有相关性，二者表征效果有所差异是因为超声法评价的是全厚度方向的应力叠加效果。

实测所得声速极差与变形量之间呈非线性递增关系，如图9 所示。实测极差结果为5～14 m/s，仿真结果为0～14.7 m/s。可以看到：1#和2#的仿真与实测结果差距较大；1#试样在材料无应力时实测仍有5 m/s 的声速变化，是由于材料的均匀性而导致固有的声速变化；2#实测结果与仿真结果有差距是因为当变形量很小时，应力太小，引起的声速变化小，声速差变化小于采样间隔，无法测得，所以得到的还是固有的声速变化；3#、4#结果较为接近，5#最为接近，仿真与实测结果所得的变形量与声速极差曲线基本一致。

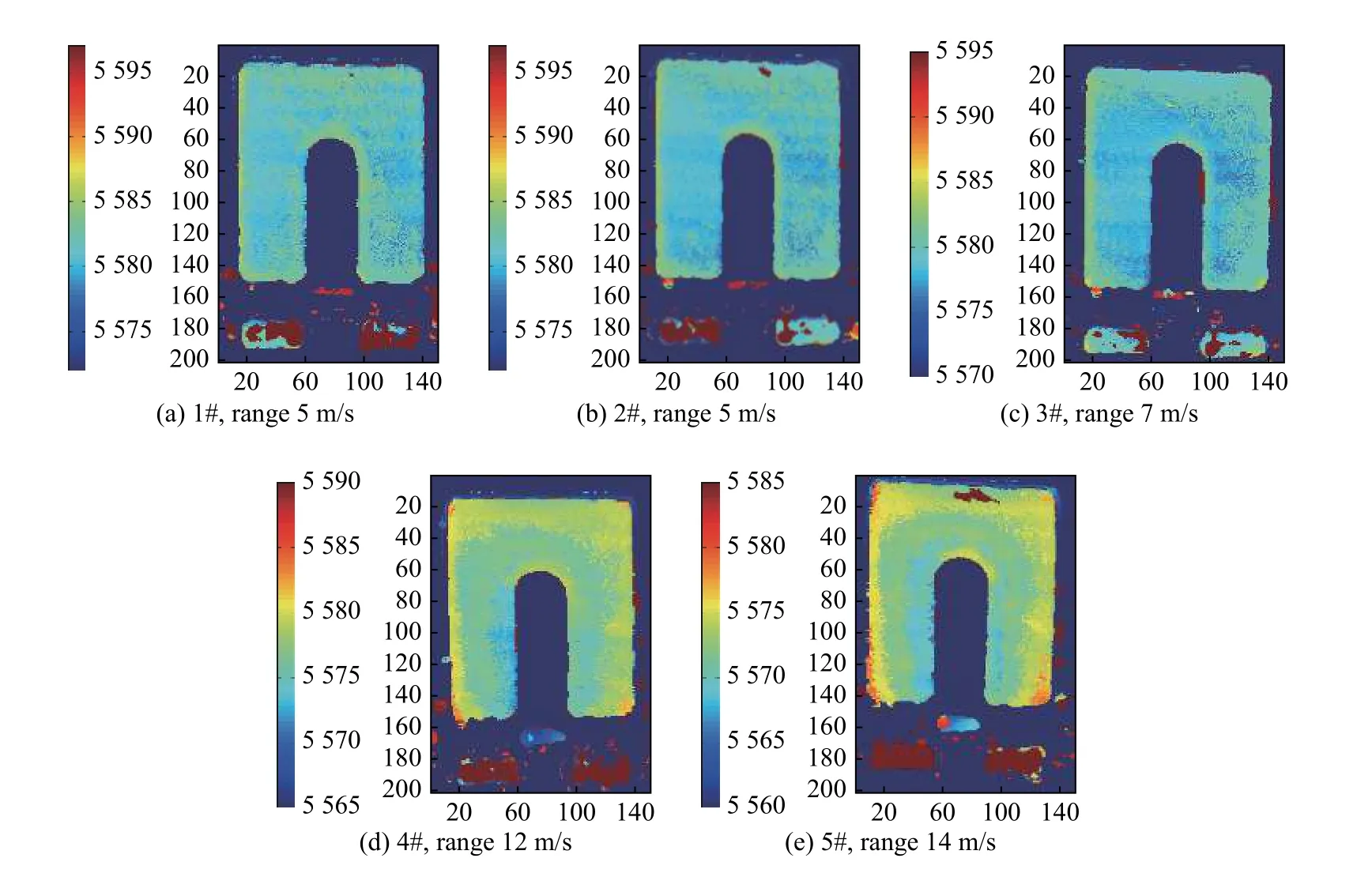
图 8 外加非均匀应力场中的声速Fig.8 Sound velocity in external non-uniform stress field

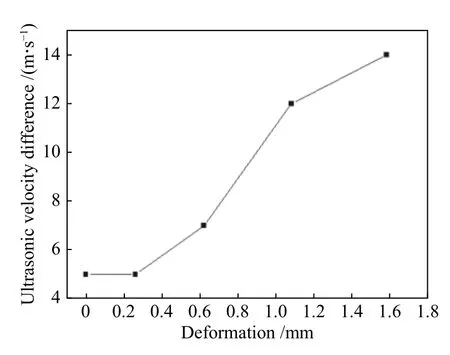
图 9 声速差与变形量呈非线性递增关系Fig.9 Nonlinear increasing relation between ultrasonic velocity difference and deformation

4 结论

1）各位置的声速差异与外加变形量具有非线性递增关系，超声法获得的应力分布结果都符合应力分布的一般规律，超声法表征结果与仿真表征结果具有相关性，但是由于超声法评价的是样品全厚度方向应力的叠加效果，所以二者又存在一定的差异性。

2）通过计算得到该模型中应力场声速极差，结果与超声应力测量变化规律较为一致，二者所得极差不同是因为材料无应力时因为材料的均匀性会导致固有的声速变化，而应力过小时，声速变化小于采样间隔，无法测量，2 种方法所得的变形量与声速极差曲线基本一致，声速极差可能成为评价样品整体应力的新指标。