基于扩展有限元的Q345R 材料平板裂纹扩展模拟研究

殷金泉 ， 程强强 ， 于润桥

（1.赣州市特种设备监督检验中心，江西 赣州 341000；2.无损检测技术教育部重点实验室（南昌航空大学），南昌 330063）

0 引言

材料的断裂或失效问题与裂纹的产生、扩展有着密切的关系，所以在工程材料设计中，对材料裂纹扩展进行数值模拟，了解裂纹的起裂与裂纹的扩展规律显得尤为重要[1-2]。在断裂力学中，裂纹的扩展通常要经历裂纹的起裂、外部施加载荷导致裂纹扩展，以及裂纹扩展后材料发生断裂一系列的过程[3]。在对裂纹的数值模拟中，较常用的方法是有限元分析。有限元方法实际上就是将物理模型分为有限个相互连接的单元组合体。与其他数值模拟方法相比，有限元方法具有易实现编程和不受材料类型、几何形状等限制的优点[4]。因此，在对连续介质力学问题进行研究的过程中，通常选择有限元方法作为主要的数值分析方法[5-6]。但当遇到对某些特殊问题的求解分析时，尤其是间断问题，有限元方法会有一些不足之处[7-8]。

为了更好地处理裂纹扩展时产生的间断问题，Belytschko 等[9]提出，在有限元基础上加入扩充形函数来描述裂尖，使得模拟裂纹扩展更加行之有效。Moës 等[10]将上述方法定义为扩展有限元法（Extended finite element method，XFEM）。运用扩展有限元方法，在模拟裂纹扩展时，裂纹不再只能沿着网格边界扩展，网格的内部也能允许裂纹穿过，而且在较粗的网格划分基础上也能获得较高的精确度，减少了很多工作量，节约了大量的计算成本。凭借其在处理断裂问题时特有的优势，可以方便地模拟出裂纹扩展过程，对材料的断裂模拟具有重大的作用和意义，可以有效的减少因为材料断裂或失效所引发的一系列事故。国外在该领域的研究已经较为成熟。Daux 等[11]利用扩展有限元法对裂纹分叉的过程进行了模拟；Fries 等[12]为了解决不连续问题，在扩展有限元方法的基础上引入局部网格细化与悬点两种方法，通过依据改进的自由度和悬点这两者之间是否联系来作为判定条件，进而选择上述两种方法的其中一种；Stolarska 等[13]则将水平集法作为一种追踪裂纹运动的数值方法引入到扩展有限元中，从而对不连续面的几何特征可以利用水平集法进行准确的描述；同年，Sukumar 等[14]在对含孔洞等不连续问题的模拟求解过程中运用了扩展有限元法；Réthoré等[15]在对动态裂纹扩展建立模型时，同样利用了扩展有限元法，并在此基础上对线性条件下数值算法的稳定性给出了证明，他们的研究显示，利用扩展有限单元法能够在符合能量守恒定律的前提下对单元进行一系列改进，由此在裂纹扩展过程中发生的能量转移均是可控的；Baietto[16]模拟了接触疲劳的裂纹扩展，基于二维、三维接触疲劳试验以及摩擦裂纹的经验公式来建立扩展有限元模型，这种模型通过直接构造水平集机制来对裂纹形状进行描述，进而可以量化出应力强度因子，最终无论是对二维或是三维的接触疲劳裂纹扩展数值模拟结果都令人满意。在国内，目前对扩展有限元的研究还处于初始阶段。夏晓舟等[17]在扩展有限元理论的基础上提出指数型间断函数，这个指数型间断函数代表任意一点到间断处的垂直距离随着距离的增大而发生指数衰减，更好地描述间断处的位移不连续；杜成斌，应宗权等[18]做了单轴受拉的颗粒增强复合材料的模拟；余天堂[19]使用扩展有限元法模拟三维裂纹，他们通过在有限元的位移模式中引入一个基于单位分解的跳跃函数和裂尖加强函数来描述裂纹处位移的不连续，并通过三维模拟算例验证了该方法的可行性；庄茁等[20]将三维最大能量释放率作为裂纹扩展准则，可以模拟各种三维裂纹扩展问题，他们还提出基于连续壳单元的扩展有限元格式，能有效模拟连续体壳类上各种裂纹扩展问题，模拟结果表明，曲面壳体内裂纹的扩展路径与单元网格的边界划分没有联系，尖端应力场被精确捕捉，证明了这种基于壳类单元的扩展有限元格式具有一定的优越性。

Q345R 钢是压力容器专用材料，具有优良的综合力学性能和工艺加工性能，屈服强度为345 MPa。裂纹是导致压力容器失效和破坏的首要原因，在压力容器检测和维护过程中，模拟裂纹的产生和发展过程，并对结果进行分析具有重要的意义。本研究讨论的裂纹扩展即是一种间断问题，采用有限元方法进行分析，会造成局部的网格加密，而其他地方变得稀疏，导致网格呈现非均匀分布，更小的网格尺寸会增加计算成本和工作量。故引入扩展有限元方法，在不大幅增加计算成本的前提下，对裂纹的扩展路径进行更加详细贴切的模拟，以及在较粗的网格划分基础上对裂纹的位移场渐进解获得精准解答。

本研究在扩展有限元的框架下，通过引入满足裂尖单元剖分性质的扩充形函数，来增强构造裂纹尖端的非连续性结构，达到对裂纹扩展过程中裂纹尖端场的精确捕捉目的，并分别对Q345R钢的有限大二维平板低周疲劳裂纹，以及二维平板中心裂纹进行裂纹扩展模拟研究，同时将时间作为自变量，主要对裂纹扩展中存在于裂纹周边的应力应变的变化情况进行分析，总结模拟裂纹的扩展规律。

1 扩展有限元基本原理

有限元方法分析不连续问题时，比如裂纹的扩展，需要在裂纹尖端应力集中区重新划分高密度网格以达到较为精确的分析计算结果。与之不同，扩展有限元方法则不需要重构网格，裂纹可以从单元内部穿过，在较粗的网格划分基础上就能得到较精确的结果。其中心思想就是采用带有不连续性质的扩充形函数描述计算域的尖端，它的基础就是单位分解[21]。

基于单位分解的扩展有限元可以表示为[22]：

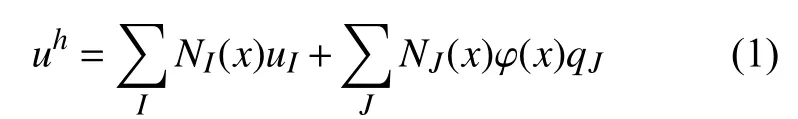
式中： uh表 示未知场； NI(x) 为标准有限元的形函数； uI为 标准节点自由度； qJ为新增加的单元节点自由度。

从式（1）可知，扩展有限元法就是在标准有限元基础上再添加扩充项用于改进对未知场的描述。通过在单元节点上引入了多余节点自由度，新增加的节点自由度依然在原单元节点上，便于方程的求解。

具体求解时可构造扩充形函数，而最常用的就是水平集函数。它的功能是用来追踪间断运动（裂纹扩展等）。下面利用水平集函数描述裂纹面的位置。

首先，用符号距离函数构造水平集函数：

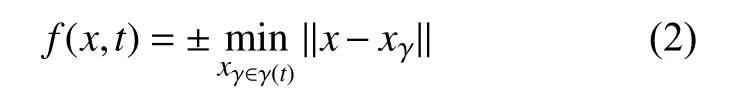
符号距离函数表示在计算域内任何一点到间断的最短距离，这个函数具有水平集函数的基本特征。式（2）中： f(x,t)的绝对值为点距离间断界面的距离；正负则取决于该点位于裂纹的哪一侧，如果位于γ(t)所定义的裂纹面上侧，则取正号，反之则取为负号。由于使用这个函数还不能反映裂纹尖端的位置，所以还需要定义一个水平集函数g：

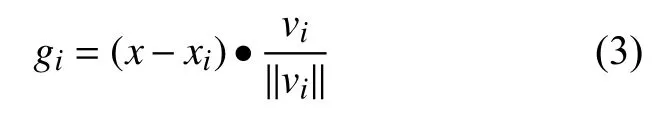
式中：xi代表端点；vi为移动速度。

这个函数表示在gi=0 时，代表一条经过端点，与裂纹移动速度垂直的直线，这条直线描述了裂尖的位置。由式（2）、式（3），裂纹面的位置则可以表示为：

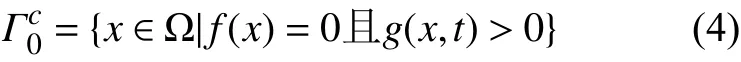
扩展有限元在描述裂纹尖端和裂纹面时添加裂尖加强函数和裂纹面跳跃函数，通过这两种函数的补充可以使得对裂纹扩展的模拟过程更加精准。裂纹面加强节点示意图如图1 所示，圆形代表阶跃扩充节点，三角形代表裂尖扩充节点。

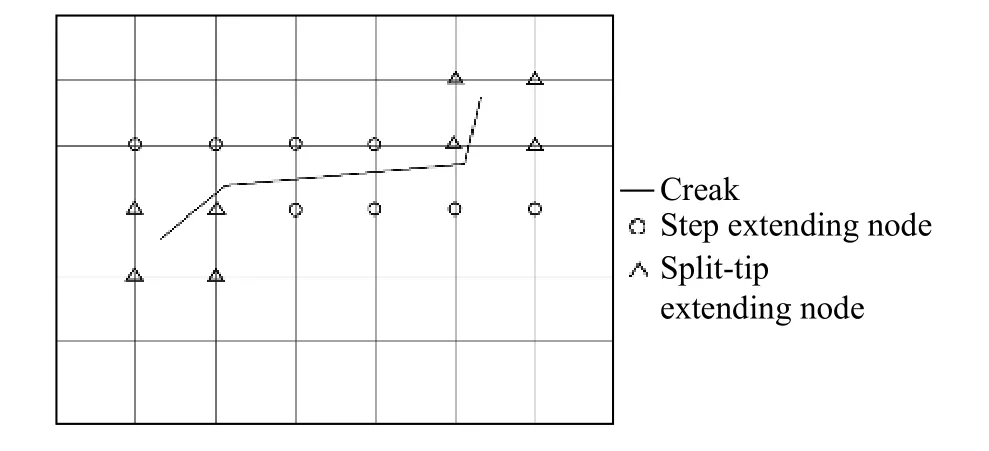
图 1 裂纹面加强节点示意图Fig.1 Schematic diagram of the crack face strengthening node

使用裂尖加强函数和裂纹面跳跃函数，裂纹的位移场就可以表示为：

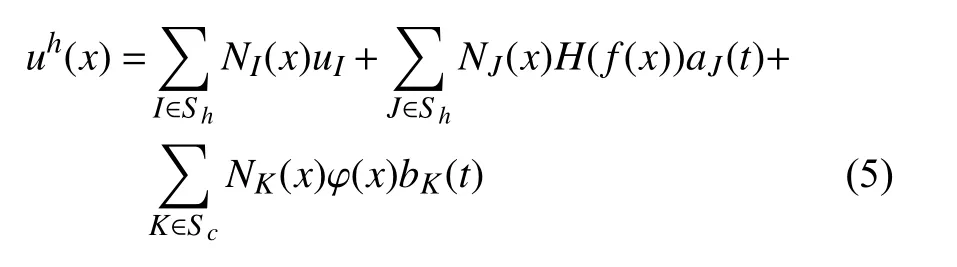
式中：第一项是常规有限元的位移函数；第二项是裂纹面跳跃函数，其中阶跃函数H(x)：

第三项是裂尖函数，用来描述裂尖的奇异性，其中：

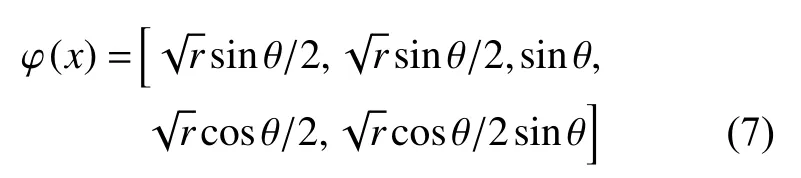
式中，θ,r 是在裂纹尖极坐标系定义的位置参数。

2 Q345R 钢板裂纹扩展模拟

2.1 有限大中心裂纹的扩展模拟

二维平板尺寸为70 mm×100 mm，材料弹性模量为70 kPa，泊松比为0.33，设置最大主应力为100 MPa 作为损伤起始判据。固定二维平板的下端，对上端施加位移载荷，模拟该二维平板中心裂纹在拉伸状态下裂纹的扩展过程，结果如图2所示。

从图2 中可以看出，当裂纹发生扩展时，裂纹的扩展路径从单元内部穿过，这和扩展有限元方法完全对应。裂纹在扩展过程中，随着载荷逐渐增加，裂纹逐渐扩展，最后导致二维平板完全断裂。通过对裂纹各区域对应的云图分析，可以看出在裂纹扩展过程中，应力集中出现在裂纹扩展的尖端，应力的最大值同样位于裂纹尖端处，裂纹面处应力值最小，这是因为裂纹面是自由端边。裂纹面两端的应力沿着裂纹两个尖端的中轴线呈分布对称，从裂纹尖端向裂纹两边的延展过程中各处的应力值逐渐减小，应力分布的趋势是符合断裂力学理论的。这进一步证明了扩展有限元模拟裂纹扩展的可靠性与准确性。

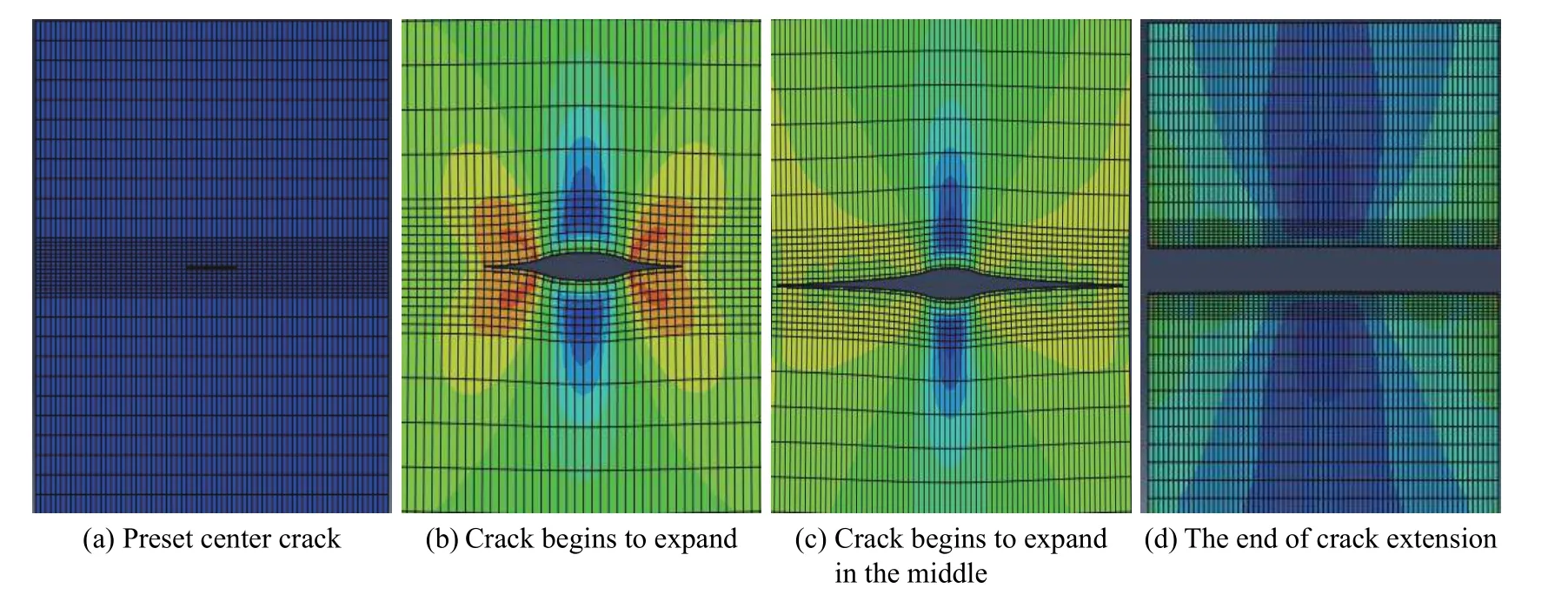
图 2 中心裂纹扩展过程云图Fig.2 Cloud pattern of the central crack propagation process

选取右边裂纹尖端的一点，绘制该点在裂纹扩展过程中应力随时间变化的曲线图，如图3 所示。由图3 可知：在施加载荷的初始阶段，裂纹尖端单元节点的应力随着载荷的增加而增大，并近似成线性关系，在这个阶段内，裂尖单元的应力并没有达到损伤判据的临界应力，所以该单元没有开裂；随着载荷的继续增加，应力值也继续增大，当载荷加载时间约0.12 s 时，裂纹尖端单元节点的应力值达到最大，裂纹开始起裂；在裂纹达到完全裂开的过程中，裂纹尖端应力变化与时间成线性关系，以恒定速率平稳下降，最终裂纹尖端应力值降为0。该单元处的应力奇异性消失，裂尖单元也由此转化为一个常规的原始划分单元。

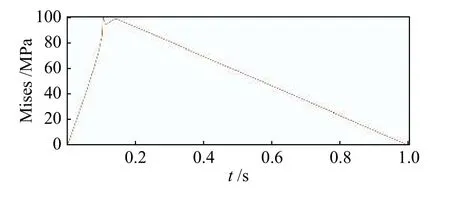
图 3 中心裂纹尖端应力曲线Fig.3 Center crack tip stress curve

图4 为裂纹尖端应变随时间的变化曲线。从图中可以看出，裂尖单元整个断裂过程的应变曲线和应力曲线类似，变化规律基本相同。在未达到最大主应力的时候，裂尖单元应变随时间增加而迅速增大，约在0.10 s 时达到最大应变值，裂纹呈开裂状态，此时应变不增反而急剧减小。之后裂尖应变随时间线性减小。单元最终变成一个普通的初始划分单元。

图 4 中心裂纹尖端应变曲线Fig.4 Center crack tip strain curve

2.2 单边裂纹（低周疲劳）的裂纹扩展模拟

平板材料尺寸为300 mm×300 mm，弹性模量为220 GPa，泊松比为0.3，最大主应力设置为88.4 MPa 作为损伤起始判据，材料的顶部与底部受到方向相反的循环变化载荷，载荷循环20 次，顶部受到峰值为8×10−5m 位移载荷，底部受到峰值为−8×10−5m 位移载荷。二维平板中心线左端存在一条长度为30 mm 的横向预制裂纹。裂纹扩展模拟结果如图5 所示。

从图5 可以看出，在低周疲劳裂纹的扩展过程中，裂纹尖端处的应力值最大，而裂纹面处应力值最小，裂纹扩展方向处应力逐渐增加，整个过程中，应力值都是沿裂纹扩展方向对称分布的。应力分布的趋势是符合断裂力学理论的。

图6 是以平板中一个裂纹尖端点为参考点，绘制出的裂纹尖端点的应力变化曲线。由图可知，该点的应力上下波动，波动曲线与低周循环载荷形状相似，约5.5 s 后，裂纹扩展到该点，应力值达到最大，为3.48×108MPa；在6 s 以后，应力值接近0，表示该点已经完全断裂。

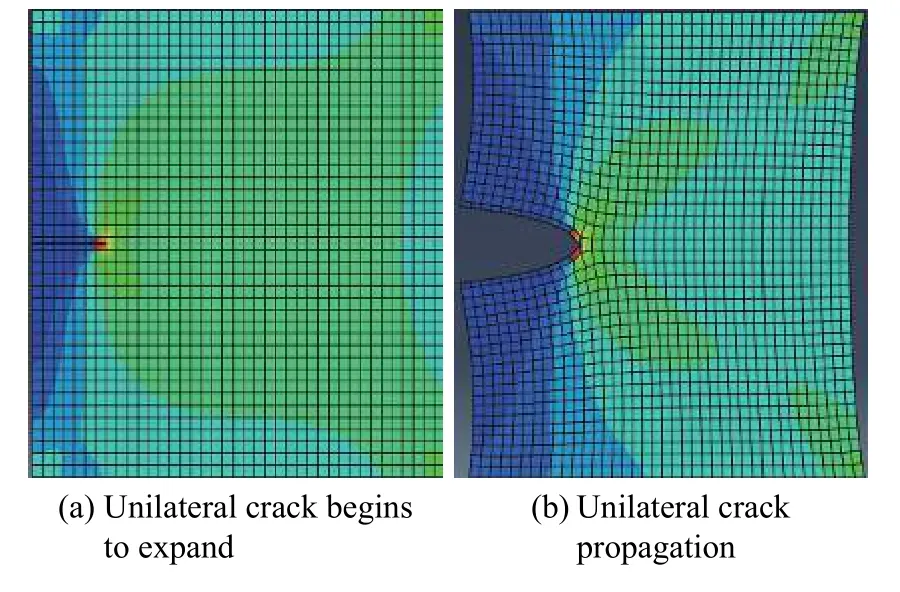
图 5 单边裂纹扩展过程云图Fig.5 Cloud diagram of the unilateral crack propagation process

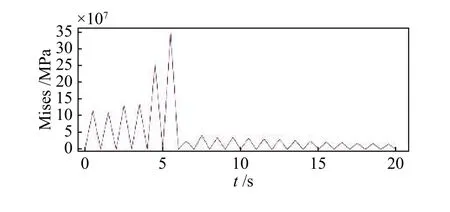
图 6 单边裂纹尖端应力变化曲线Fig.6 Single edge crack tip stress curve

裂纹尖端点的应变变化曲线如图7 所示。裂纹尖端的应变曲线与应力变化曲线类似，由于是在周期载荷作用下，该点处的应变先上下波动，在5.5 s 时在达到最大值，在6 s 以后，应变值降为0，表示该点已经完全断裂。

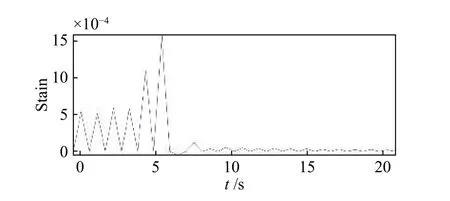
图 7 单边裂纹尖端应变曲线Fig.7 Single-edge crack tip strain curve

2.3 与常规有限元模拟方法的比较

为了进一步说明本研究方法在裂纹扩展模拟上的有效性和准确性，将模拟结果与常规有限元模拟的裂纹扩展过程进行对比。屠立群等[23]运用有限元分析软件Ansys 模拟了单边裂纹扩展过程，结果如图8 所示。对比图5、图8 可以看出，运用常规的有限元方法模拟时，由于难以对裂纹边界的扩展进行准确模拟，裂纹扩展的边界呈直线状。而采用扩展有限元方法时，采用扩充的加强函数来准确地表达边界的扩展，可以准确有效地模拟出边界扩展的非线性。这与实际裂纹的扩展过程[24]相吻合、一致。

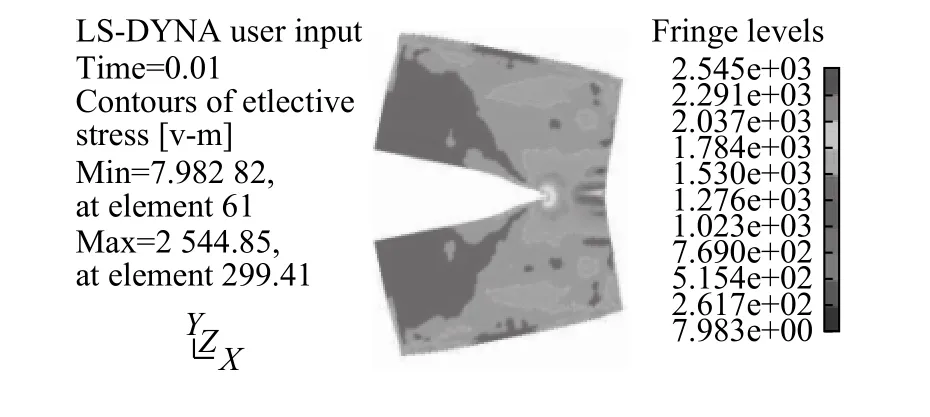
图 8 常规有限元方法裂纹扩展过程云图[23]Fig.8 Cloud diagram of crack growth process with conventional finite element

3 结论与展望

1）从模拟的裂纹扩展云图数值分析中可以发现，裂纹尖端处会在裂纹扩展的过程中出现应力集中，中心裂纹和单边裂纹这两种不同的裂纹应力变化规律相似，在未达到最大主应力的载荷施加阶段，裂纹尖端应力不断增大，但裂纹并未发生扩展；施加载荷达到最大主应力后，裂纹呈开裂的状态，应变进而急剧减小，最终变为0。这种变化和断裂力学是符合的，应力分布趋势与通过理论方法计算确定的塑性区相符合，因此进一步有力地证明了利用扩展有限元方法对 Q345R 材料中裂纹扩展过程模拟分析的可靠性和有效性。

2）与常规有限元方法比较，本研究方法可以更加准确和有效地模拟边界扩展的非线性。下一步拟将扩展有限元方法运用于三维物体断裂和裂纹扩展问题，进一步拓宽该方法的应用领域。