试探长方体法构图 提升直观想象学科素养
李 阁
(辽宁省实验中学东戴河分校 125200)
一、从课本上的例题试探
人教B:P53例4:已知:如图1,平面α⊥平面β,在α与β的交线上取线段AB=4 cm,AC,BD分别在平面α和平面β内,它们都垂直于直线AB,并且AC=3 cm,BD=12 cm,求CD的长.
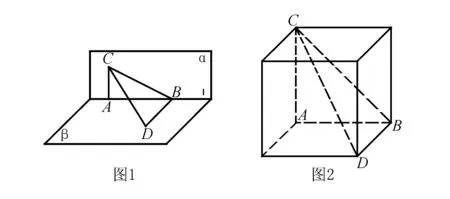
探索分析根据题意我们可以发现,AC⊥AB,AC⊥BD,BD⊥BA,BD⊥BC.根据图形及结构,我们可以将几何图形抽象出来放到下面的长方体里,以长方体为“母体”,能够很容易培养学生形成直观抽象的空间关系,有利于我们处理长度关系.如图2,那么我们就可以将求CD的长的问题转换为求长方体体对角线的长.
二、从课本上的习题试探
人教B:P57习题1-2B第8题:已知:如图AB是圆的直径,PA垂直圆所在的平面,C是圆上任一点.求证:BC⊥平面PAC.
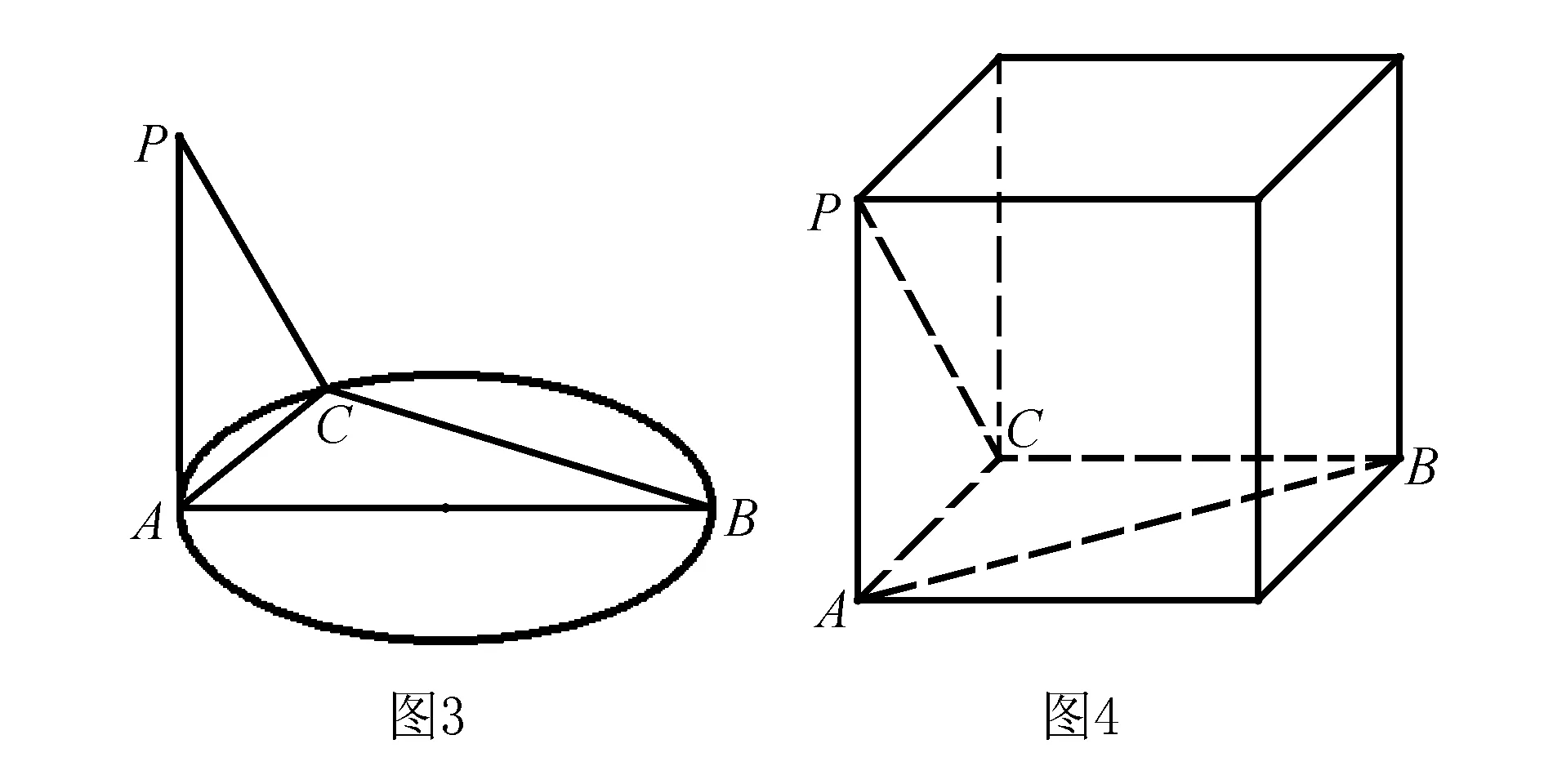
探究分析根据题意我们可以发现
∠ACB=90°,PA⊥AB,PA⊥AC,PA⊥BC.
根据空间几何结构,我们还可以很将几何图形抽象出来放到下面的长方体里,如图4.
可以看出线线之间的关系(如上面的分析),如还可以看出线面之间的关系(如BC⊥平面PAC),以及面面之间的关系(如平面ABC⊥平面PAC),如果再加上一些边长的关系,那么还有利于解决异面直线所成角的一些问题.
三、从翻折问题上试探
如图5,边长为2的正方形ABCD中,点E、F分别是AB,BC的中点,将△AED、△DCF分别沿DE、DF折起,使A,C两点重合于点A′,求证:A′D⊥EF.

探索分析我们可以发现在折起之前AE=CF,折起之后A′E=A′F,且DE=DF,同时∠B=90°,且四边形ABCD为正方形,这些条件可以从充分地将几何体置于长方体中.
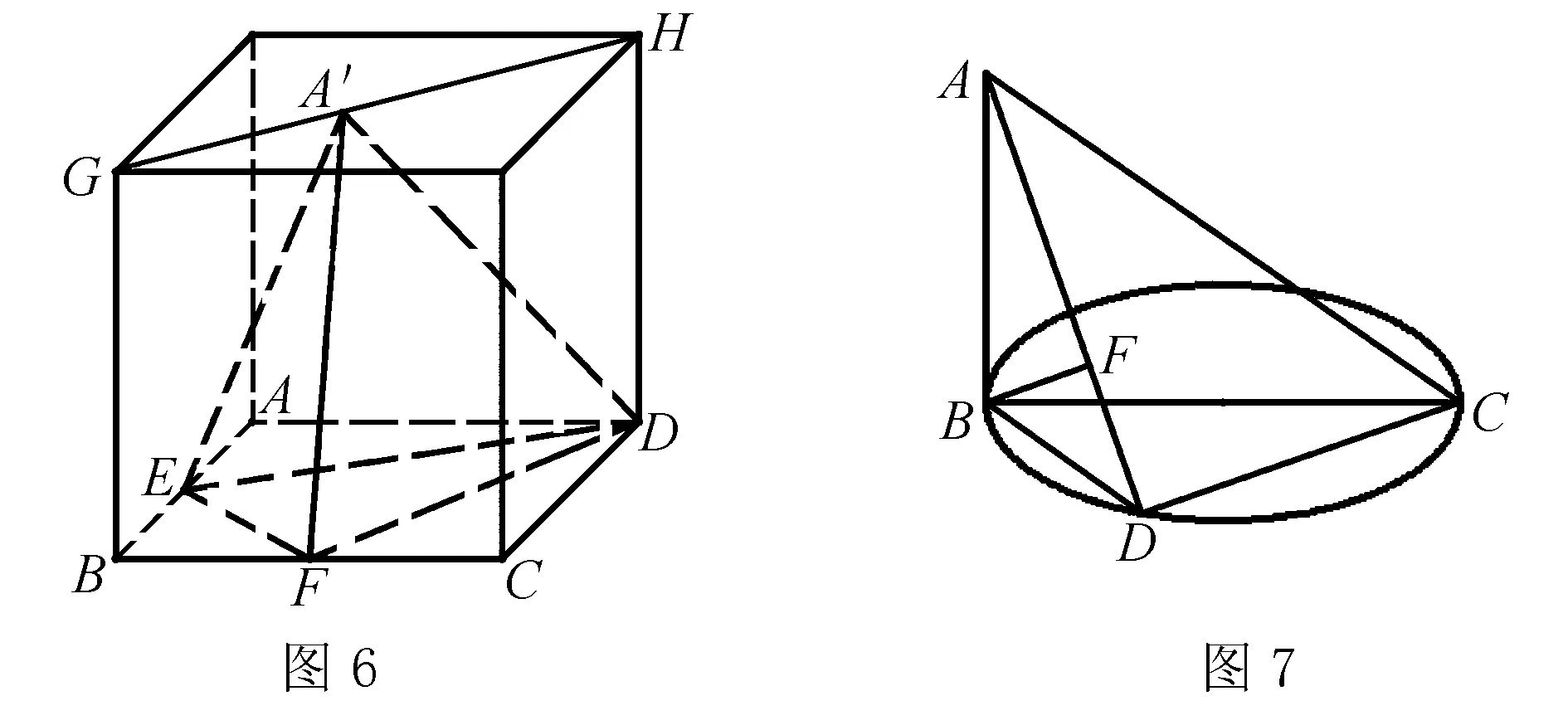
如图6:借助于四边形ABCD为正方形,直接就成为一个正四棱柱的底面,再结合A′E=A′F,则可以将A′置于上底面对角线GH上,这样所有的条件就可以满足.
这样证明A′D⊥EF问题的过程中是不是即解决了立体几何的抽象问题,再结合线面垂直的判定定理及线面垂直的定义,又解决了逻辑思维问题及答题的规范性呢?
四、从各地检测题上试探
2015,河南信阳市高一期末测试:如图7所示,BC是圆O的直径,AB垂直于O所在的平面,D是圆周上异于B,C的任意一点,BF⊥AD,点F为垂足,求证:BF⊥平面ACD.
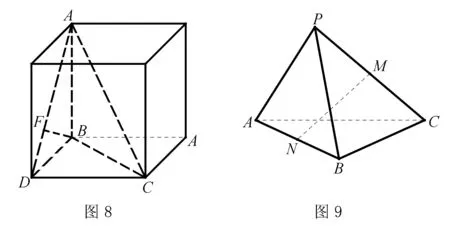
探索分析通过对上面人教B:P57习题1-2B第8题的分析,这样的空间几何体现在就很容易将它放入到长方体中了.如图8,因为BC是圆O的直径,所以∠BDC=90°,BD⊥DC,又因为AB垂直于O所在的平面,所以AB⊥BD,AB⊥DC,AB⊥BC.又因为BF⊥AD,点F为垂足,所以从直观上很容易得到DC⊥BF,那么BF⊥平面ACD利用线面垂直的判定定理也就唾手可得.
五、从创新性试题上试探
如图9,在△ABC中,∠B为直角,P是△ABC外一点,且PA=PB,PB⊥BC,若M是PC的中点,试确定AB上点N的位置,使得MN⊥AB.
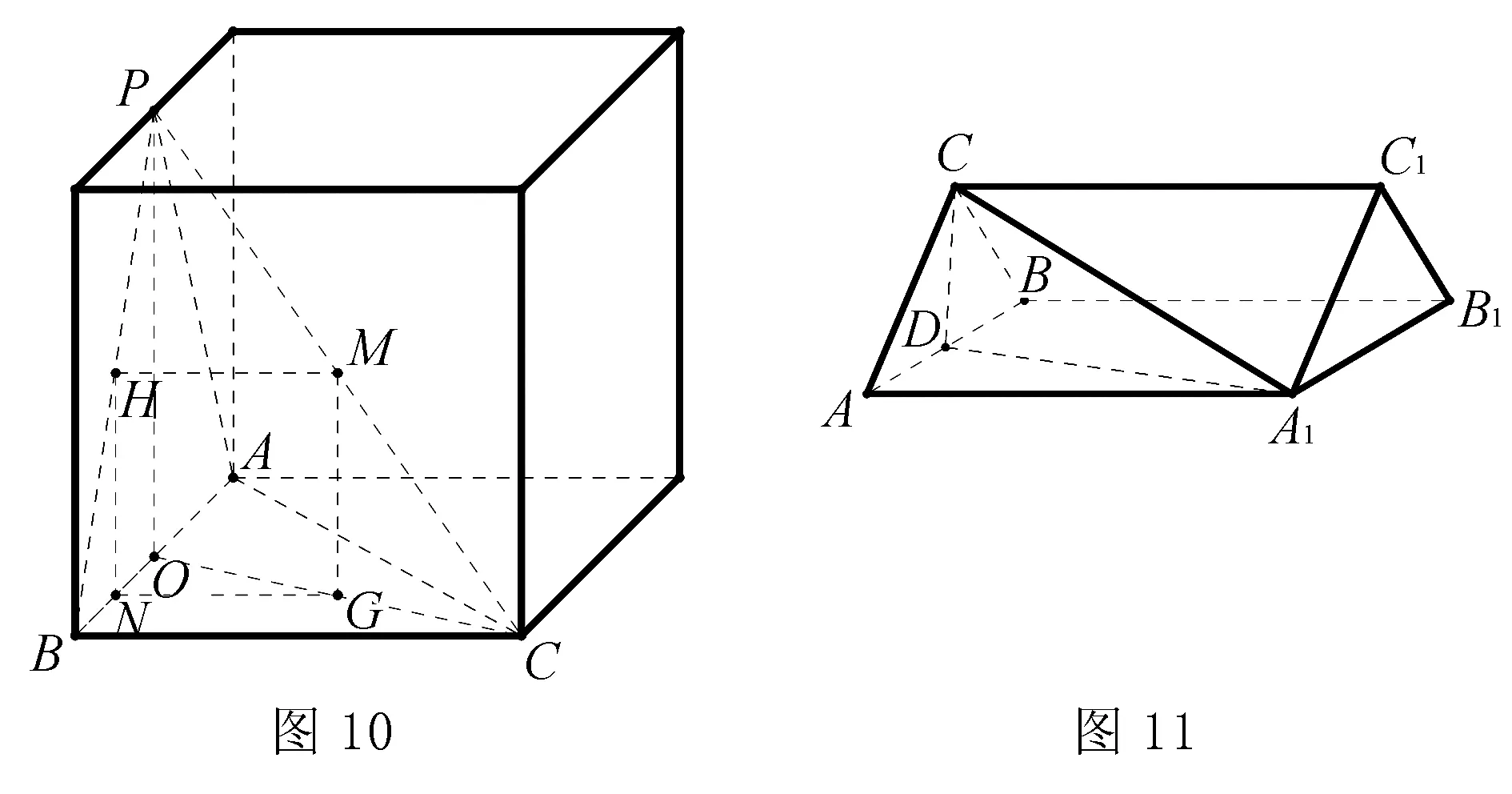
探索分析此题我们依然可以类比人教B:P57习题1-2B第8题的分析,因为在ΔABC中,∠B为直角,所以可以认为∠B为长方体的一个底面长方形的直角,又因为P是△ABC外一点,且PA=PB,PB⊥BC,所以,我们可以将点P置于长方体的一条棱的中点,这样PA=PB的条件就可以满足,又因为PB⊥BC,所以很容易想到点P所在的棱是与AB所对的棱上,这样就可以满足所有题目中的条件了.如图10.
在转换的过程中,图形看得清楚了,我们只是换了个角度看问题,但是在转换的过程中,我们不但复习了一些几何知识,还能将问题解决,提升抽象能力,我觉得长方体还是很实用的.
六、从高考试题上试探
(2013年新课标1卷)如图11,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,D为AB中点,∠BAA1=60°.
证明:(1)AB⊥A1C;(2)若平面ABC⊥平面AA1B1B,AB=CB,求直线A1C与平面BB1C1C所成角的正弦值.
探索分析根据上面的各类问题中,要想将空间几何体与长方体相结合,必然有很多的垂直关系作为依据,才能将问题转化的贴切,而这道高考题中没有那么多的垂直关系,那么又将如何转化呢?
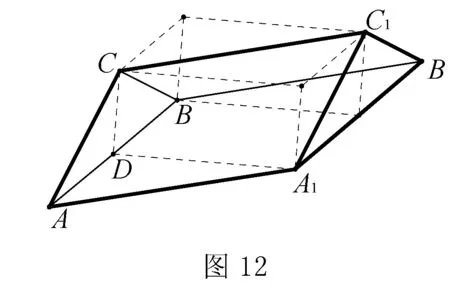
如图12,这个长方体的引入有些不同了,因为我把它延伸了,才能与这道题相匹配,首先AB⊥面A1CD,那么我们才有:AB⊥A1C, 这可以认为是长方体中的一条棱与一个面之间的关系,而∠BAA1=60°,所以将BD延长了,结合CA=CB是可以构造出∠BAA1=60°.可是又缺少∠CDA1是直角,但是在第二问中有平面ABC⊥平面AA1B1B,这样我们就可以将几何体结合长方体了,但是如果只是在第一问中是不能确定∠CDA1是直角,但这也是只给第一问的一种特殊情况.可是如果结合第二问,将几何体结合长方体,那么我们很容易直观地看出直线A1C与平面BB1C1C所成角为∠CA1D,结合三角函数,那么正弦值就得到了.
在上面的研究中我们可以发现很多的几何体是可以与长方体作为“母体”相结合的,但是要满足一些直角和边相等的关系,同时还要结合课本中的理论认识.这种直观抽象与数学抽象的学科素养是需要不断培养的,很多的事物都是在不断的发展与变化的,在不断的发展与变化中,需要我们不断地去探索与研究.在人教B必修二的第一节内容就是“构成空间几何体的基本元素”中就是以长方体为例,初步让学生直观感受点、线、面的位置关系,那么教材的这样设计是不是也有编者的一些想法呢?或者出题人也有这样的认识呢?但不管怎样,深入挖掘教材,“用教材教,还是教教材”,这句话让人深省.

