一道用微元法求解物理题的推广
韩福济
(湖北省武汉市华中科技大学附属中学 430074)
一、题目及微元法
例1 如图1(a),一质量为m的均匀闭合细绳套在一光滑铁圆锥上,铁圆锥半顶角为α,求解当细绳平衡时,绳中的张力为多少?
分析:细绳在光滑铁圆锥上的每点受力相同,如以整个细绳为研究对象,则问题变得很难,而将细绳用微元法化为小的微分弧段,也可以认为是质点为研究对象,就可以分析其受力,从而将问题迎刃而解.
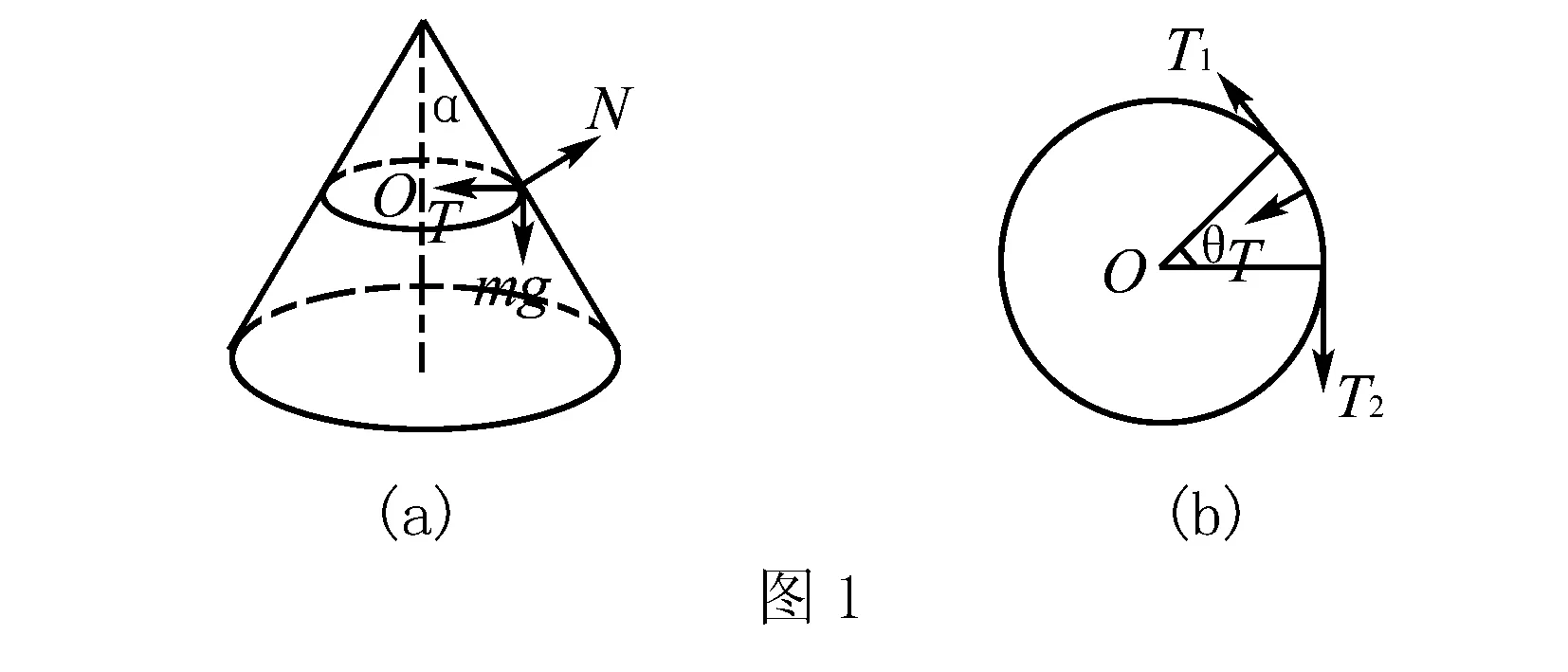
解将细绳划分为n个小弧段,取其中的一个弧段微元为来研究.
假设绳圈的半径为R,这个小弧段的圆心角为θ,质量为Δm,微元的受力分析如图1(b)所示:重力为Δmg,弹力为N,合力为T,有平衡条件得到下列式子:
(1)N·cosα=T,N·sinα=Δmg.
现在设微元弧段的两个端点的张力分别是T1、T2,并且它们的大小相等,其合力T,方向指向原点O. 由力的分解可知:

并且由于绳圈是均匀的,所以有
联立(1)(2)(3)式,得到:
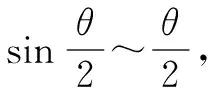
二、将圆锥体推广为光滑铁球体
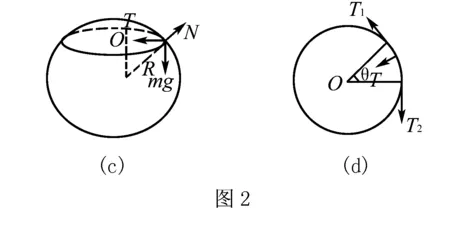
例2 如图2(c),一质量为m的均匀闭合细绳套在一光滑铁球体上,铁球体的半径为R,绳套的长度为L,且绳套长度小于球的大圆周长. 求解当细绳平衡时,绳中的张力为多少?
分析1 类比于例1,进行分析计算.
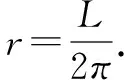
重力为Δmg,弹力为N,合力为T,有平衡条件得到下列式子:
现在设微元弧段的两个端点的张力分别是T1、T2,并且它们的大小相等,其合力T,方向指向原点O. 由力的分解可知:
并且由于绳圈是均匀的,所以有
联立(5)(6)(7)式,得到:
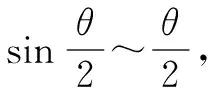


分析2 在球体上,假设有一个圆锥体相切于绳套处,如图3. 则问题转化为例1中的圆锥体上绳套的张力问题,就可用例1的结果.
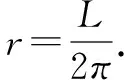
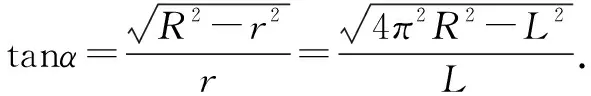
所以利用例1的结果就得到所求的绳子的张力为
三、将圆锥体推广为更一般的旋转体
例3 如图4,一质量为m的均匀闭合细绳套在一光滑的花瓶上,花瓶表面是一个旋转体的表面. 旋转体表面是由函数y=1-x2绕着y轴旋转一周得到的,绳套的长度为L. 求解当细绳平衡时,绳中的张力为多少?

分析在这个花瓶上,也同样假设有一个圆锥体相切于绳套处,如图4. 则问题转化为例1中的圆锥体上绳套的张力问题.
解(转化法) 假设有一个圆锥体相切于绳套处,如图4. 那么铁球体上绳套中的张力就变为圆锥体上的绳套的张力问题. 所以只需要求出相切的圆锥体的半顶角α即可.
所以利用例1的结果就得到所求的绳子的张力为
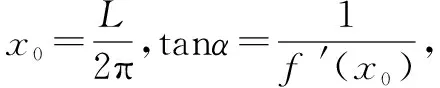
最后再留一个问题,对于更一般形状的,比如光滑的椭球体,是否有解决办法?

