f(x)=(x-b)|x-a|型函数性质
2019-02-15 08:22孙添耀
数理化解题研究 2019年1期
孙添耀
(浙江省宁波市五乡中学 315111)
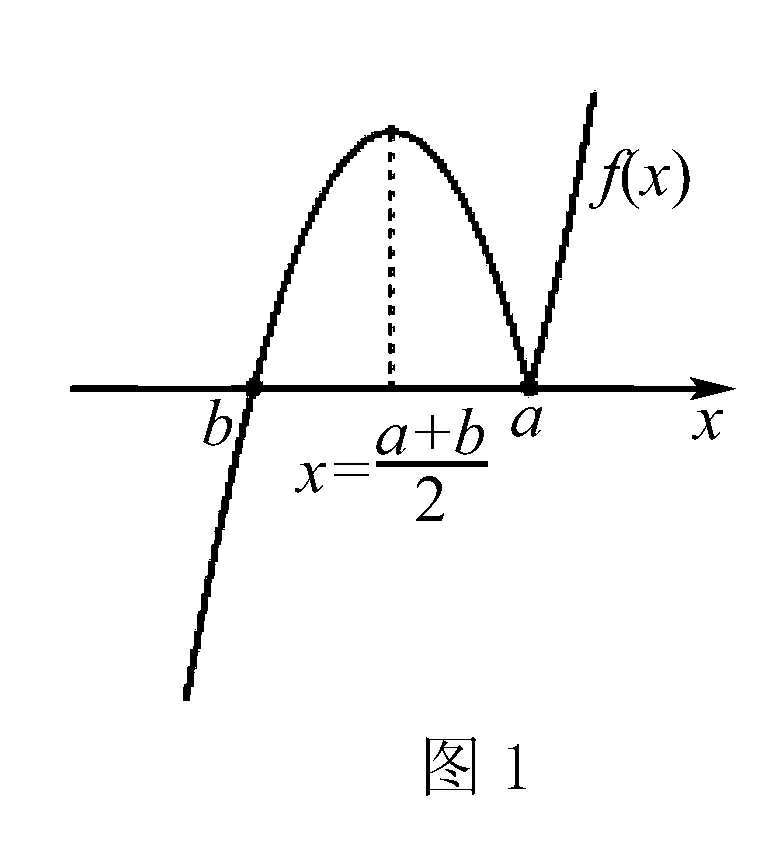
首先研究函数f(x)=(x-b)|x-a|的对称性与单调性.为了研究方便,不妨固定参数b.且讨论a>b时,函数f(x)图象如右图1:
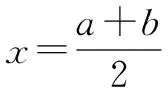
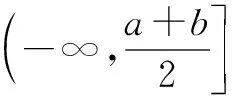
当a 接下来我们讨论a>b时函数f(x)在闭区间[0,m]上最值的问题. 不妨令b=1,m=4.求函数f(x)=(x-1)|x-a|(a>1)在区间[0,4]上的最值. 解设原函数为h(x)=(x-1)(x-a)(a>1), 根据函数对称性作图2. ∴fmax(x)=f(4)=3|4-a|=3(a-4). 故综上可得, 一般函数f(x)=(x-b)|x-a|(a>b>0)图象如图4. 在区间[0,m]上的最值作如下总结: 此时fmin(x)=f(0)=-ab. 同样要分成三种情况: ∴fmax(x)=f(m)=(m-b)(a-m) ③当m>x00时, ∴fmax(x)=f(m)=(m-b)(m-a). 故综上可得,fmin(x)=-ab,



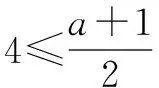






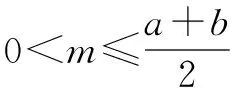

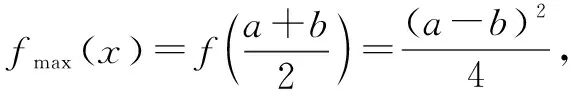
猜你喜欢
海峡科学(2021年8期)2021-11-09
郑州大学学报(理学版)(2020年1期)2020-02-08
中学生数理化(高中版.高考数学)(2019年9期)2019-11-27
中学生数理化·高一版(2019年4期)2019-01-11
中学生数理化(高中版.高二数学)(2018年11期)2018-11-29
中央民族大学学报(自然科学版)(2017年2期)2017-06-11
中学生数理化·高二版(2016年8期)2016-05-14
小天使·二年级语数英综合(2015年8期)2015-07-06
小雪花·成长指南(2014年8期)2014-08-26

