数学语言转换在解析几何中的应用

王 欣

(北京工业大学附属中学 100022)

前苏联教育学家、心理学家瓦季姆·克鲁捷茨基 (Вадим Андреевич Крутецкий)指出，数学阅读是一种从书面数学语言中获得意义的心理活动过程,是包含感知、理解、记忆等一系列心理活动以及分析、综合、推理、判断、归纳、演绎等一系列思维活动的总和.因此数学阅读能力可以定义为：学生通过在数学文字语言、图形图表语言、符号语言所呈现的信息中，提取数学信息，并能把这些信息同已有的数学知识相联系，从而分析出数学语言表达的含义，进而借助数学语言之间的转译解决问题的一种能力.对数学的学习就是对数学语言的学习，语言是思维的载体，借助数学语言之间的转换，才能获取信息，训练思维能力，解决问题.以解析几何为例，解析几何的核心是用代数方法来研究几何问题，在这一过程中，就要用到数学语言之间的转译，即把问题中的文字语言转译为图形语言，再把图形语言转译为符号语言，最终利用符号化的坐标(代数方法)，完成几何问题的求解.而向量在实现数学语言的转译过程中，发挥了桥梁的作用.向量本身就是一种符合化的语言，它既能反应图形的几何特征，其坐标表示又能方便进行代数运算，因此向量是解决解析几何问题过程中，实现用代数方法解决几何问题的重要工具.

一、问题呈现与课堂实录

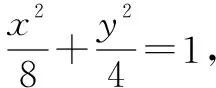
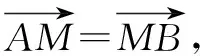
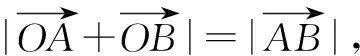
(3)以AB为直径的圆过原点O，求k的值；

(4)椭圆上是否存在一点P，使四边形PAOB为平行四边形？

(5)直线l与y轴交于N点，若|AN|=|BF1|,求k的值.

生1：不对，M、A、B三点应该在一条直线上，并且AM的长度与MB的长度是一样的，因此M是线段AB的中点.

师：回答的非常好.这位同学抓住了向量的两个要点：方向和长度，向量相等说明方向相同，模相等.这个解析几何问题的条件是以向量的语言表述的，这位同学帮助我们把向量语言对问题的描述转化为了几何图形的性质，即M为AB的中点.我们知道解析几何的核心是用代数方法来研究几何问题，现在我们已经挖掘出了这个问题的几何特征，那么我们应该如何用代数方法，即坐标来描述M为AB中点这一结果呢？

生2：设出A、B两点的坐标，联立方程，利用韦达定理求出中点M的坐标.

生3：可以用点差法，构造OM的斜率.

师：回答的非常好.这个问题我们借用向量这个工具，实现了几何问题代数化.接下来我们看问题(2),向量条件说明了什么？

生4：说明了直线OA与直线OB是垂直的.

师追问：你怎么判断的？

生4：我画了向量加法的图，发现了平行四边形的对角线是相等的,说明是矩形(并上黑板进行了演示).

师：也就是说你用了向量加法的平行四边形法则，发现了对角线相等，从而平行四边形就是一个矩形这一几何特点.那么接下来我们要怎样利用OA与OB垂直这一结论呢？

生5：斜率乘积等于-1！

生6：点乘等于0比斜率乘积是-1好，你怎么知道有斜率？

师：向量的数量积为0确实避免了讨论斜率是否存在这一问题.不知道同学们有没有发现，我们通过对已知条件中的向量语言加以分析，发现了几何性质，但是接下来的处理我们又重新转回了向量语言？我们的工作岂不是白做了？(微笑)

生7：不是这样啊，接下来我们要用坐标，用韦达定理计算啊.

师：回答的非常漂亮.我们一直强调，解析几何是用代数(坐标)方法来研究几何问题，而向量运算，恰好既有向量表达式又有坐标表达式，从而很好地搭建了代数与几何之间的桥梁，是一个很好的工具.希望同学们可以好好利用这个工具.那么接下来我们看第(3)个问题.

生8(抢着说)：咦？这是一个问题啊.

师：具体解释一下.

生8：第(3)个问题与第(2)个问题是一样的问题.以AB为直径的圆过点O，不还是说明直线OA与OB是垂直的，跟上一个问题是一样的啊.

师：说对了.但是这两个问题在已知条件的叙述上是不一样的.

生9：(3)的说法更好理解.

师：(笑)但是(2)的说法更简洁啊！(3)是用文字语言来描述一个几何特征，而(2)是用符号语言在描述这个几何特征，我们可以发现对同一个问题的描述还是符号语言更能体现我们数学的简洁美.接下来我们看问题(4),还是用文字语言来表述的几何性质，我们应该如何分析？

生10：(似乎受到了解决前面问题用向量方法的启发)，向量相等解决吧？

师：什么向量相等？

师：看了这位同学已经学会了如何用向量语言来描述几何图形的性质了，有没有其他形式的向量表示来解释平行四边形这个条件？

师：嗯！这样来翻译平行四边形这个条件，对这个问题而言，确实比较简洁，韦达定理直接就用上了.非常好.看来我们对于向量这个工具的运用已经有了一定的建树.那么我们看下一个问题，大家怎么处理？我看有些同学皱眉头，我知道你们是最不愿意处理距离问题的，公式太麻烦，计算量还大，不一定算得对，是这样吗？

很多学生笑.

师：那么有了我们前面几个问题的基础，看看我们同学有没有什么方法可以成功避免去求距离？

生12：用向量的模相等做.

生13：(立刻反对)模相等不还是长度相等.

师：说的是.我们不能为了用向量而用向量，有没有什么方法躲开求向量的模？

生14：其实就是向量直接相等就可以了.

师：为什么？

生14：因为共线啊，四个点在一条直线上，所以方向相同的话，模相等就是向量直接相等.

师：说的非常好，成功地将几何性质用向量语言准确地描述出来了，距离相等转化为了向量的坐标对应相等，实现了几何问题的代数化.

画图、计算、总结部分此处略……

二、归纳总结与方法提炼

本节课的教学设计，以向量这个工具为媒介，通过符号语言、图形语言与文字语言之间的转化，实现了几何与代数之间的转化，使学生更加深刻地体会了解析几何的本质.

以2010年北京高考题为例：

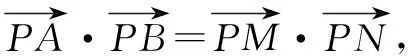
还有很多类似的，以向量为工具，实现几何问题代数化的例子.譬如A、P、B三点共线问题，用向量语言翻译，有如下可能：(1)存在非零实数λ，使得AP=λPB;(2)OP=tOA+(1-t)OB;(3)|PA||PB|=PA·PB.

归纳一下高中阶段解析几何中，一些可以被向量语言来翻译的几何模型如下：

向量条件几何关系AM→=MB→;OM→=12(OA→+OB→) M为线段AB中点OA→·OB→=0 点O在以AB为直径的圆上(或∠AOB为直角)OA→·OB→<0且OA→≠λOB→点O在以AB为直径的圆内(或∠AOB为钝角)OA→·OB→>0且OA→≠λOB→点O在以AB为直径的圆外(或∠AOB为钝角)AP→=λPB→ 或OP→=tOA→+(1-t)OB→或|PA→||PB→|=PA→·PB→A、P、B三点共线PQ→·AB→=0已知PA=PB的等腰㐷APB,取AB的中点Q,|PA|=|PB|AP→=QB→;或AB→=AP→+AQ→四边形APBQ是平行四边形AB→=AP→+AQ→且AQ→·AP→=0;或|AP→+AQ→|=|AP→-AQ→| 四边形APBQ是矩形AB→=AP→+AQ→且AB→·PQ→=0四边形APBQ是菱形OA→·OB→=12OC→·OD→S△AOB=12SΔCOD

运用向量法解决解析几何问题，并没有削弱坐标法解决解析几何问题的主体地位，因为向量运算的本质仍然是坐标运算.向量法在几何图形性质的表述上更加简洁和直接，向量兼具“数”和“形”的双重特点，借助向量在解决与共线、垂直、长度、角度等问题时，可以减少运算量，使得几何与代数的联系更加自然和紧密.

从数学本质的角度看，数学学习的过程就是发展数学能力的过程，也就是数学素养培养和构建的过程.

从信息加工的理论看，要完成上述数学学习的过程，就要完成数学信息提取与数学信息加工这两个过程.而数学信息的呈现是通过不同的数学语言来实现的，也就是说数学语言是数学内容和数学思维的载体.因此数学学习过程的实质，就是对数学语言的学习，而对数学语言的学习过程，又培养了数学思维，获得了解决问题的方法，发展了数学能力.

数学语言共分三种，文字语言、图形图表语言、符号语言，其中文字语言通俗易懂，图形语言直观形象，符号语言简洁抽象，各有所长.数学把现实生活中的量的关系、量的变化、形的特征抽象成为一个一个的数学模型，并把它们符号化，所以对数学语言的把握就要把符号化的数学知识转译成通俗易懂的文字语言或者是直观形象的图形语言.在教学过程中，教师要引导学生在这三种语言之间进行切换，转译，从而达到重新认识数学模型，或者构建新的数学模型的目的，获得新的数学知识、解决新的问题.