挖信息 巧构造
2019-02-15 08:27梁宗明
数理化解题研究 2019年1期
梁宗明
(甘肃省兰州市兰化一中 730060)
构造法就是依据某些数学问题的条件或结论所具有的典型、共同的特征,用已知条件中的元素为“元件”,用已知的数学关系为“支架”,在思维中构造出一种相关的数学对象、一种新的数学形式,从而使问题转化并解决的方法.对于一些问题,如果能准确挖掘出题目中潜藏的构造信息,恰当的构造出函数或方程,就能获得简捷、直观、有效的解答思路.
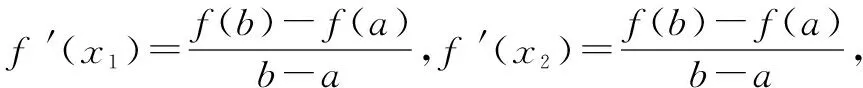
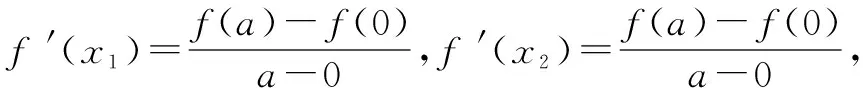
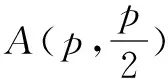
(1)求抛物线方程;
(2)过点A作圆C2:x2+(y-a)2=1的两条切线,分别交抛物线于点M,N,若直线MN的斜率k=-1,求实数a的值.
解析(1)易得x2=4y,A(2,1).
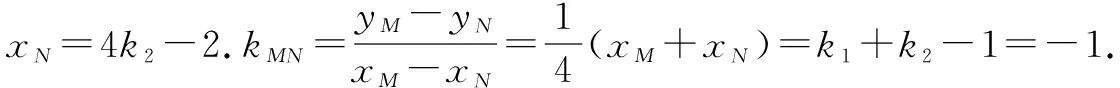
例3 已知函数f(x)=ax2-(a+2)x+lnx(a>0).
(1)求函数f(x)的极值;
(2)若点A,B是曲线f(x)上不同两点,且直线AB的斜率k>-2恒成立,求实数a的取值范围
解析(1)略.
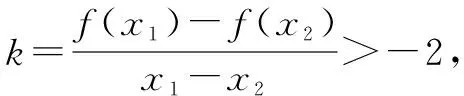
猜你喜欢
语数外学习·初中版(2022年3期)2022-05-25
中学生数理化·中考版(2021年10期)2021-11-22
中学生数理化(高中版.高二数学)(2021年2期)2021-03-19
河北理科教学研究(2020年2期)2020-09-11
语数外学习·初中版(2020年2期)2020-09-10
物理之友(2020年12期)2020-07-16
中学生数理化·七年级数学人教版(2018年3期)2018-05-30
中学生数理化·中考版(2017年3期)2017-11-09
中学生数理化·中考版(2017年10期)2017-04-23
中学生数理化(高中版.高二数学)(2017年1期)2017-04-16

