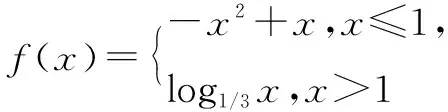数形结合一字诀
张书源
(河南省商丘市民权县高级中学 476800)
“蛮干一身汗,妙想一挥扇”.解题不可只是下苦功夫,要动点脑筋、略施小计,才能使问题得以迎刃而解.数形结合也是如此,关键时多一点思考,解题就会势如破竹,结论自然滚滚而来.
一、多一点识图画图意识
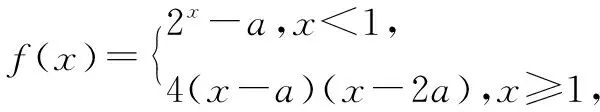
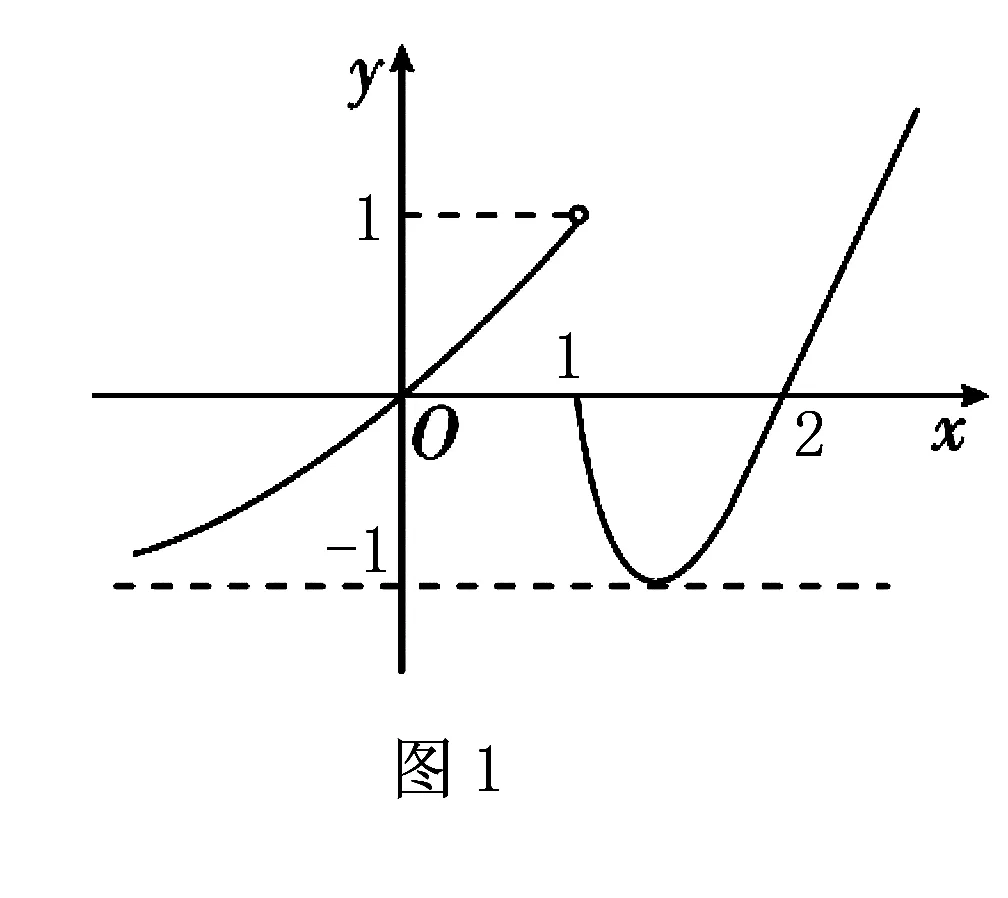
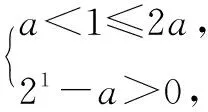
评注由于所定义的函数是分段结构,从代数量上比较倒不如从几何直观上确切,这样函数图象的信息就得到了充分的展现.
二、多一点由数想形思维
例2 已知函数f(x)=|x2+3x|,x∈R,若方程f(x)-a|x-1|=0恰有4个互异的实数根,则实数a的取值范围是____.
解设y1=f(x)=|x2+3x|,y2=a|x-1|,在同一直角坐标系中作出y1=|x2+3x|,y2=a|x-1|的图象如图2所示.
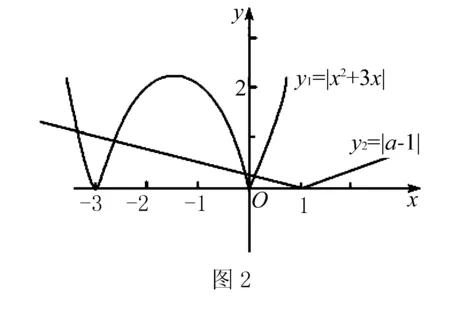
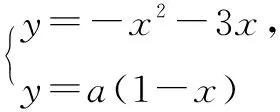
评注新的背景,依旧是老的问题.在确定了图象之后, 直接求出具体的根会得不偿失,而采用数形结合将数化为形,从数形结合的角度将不等式从几何直观上给予全新的解释,解法养眼,令人耳目一新.
三、多一点由形思数策略
例3 已知函数f(x)=2x,x∈R.
(1)当m取何值时,方程|f(x)-2|=m有一个解?两个解?
(2)若不等式[f(x)]2+f(x)-m>0在R上恒成立,求m的取值范围.
解(1)令F(x)=|f(x)-2|=|2x-2|,
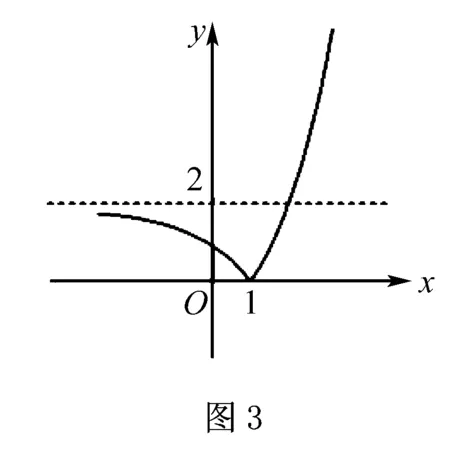
G(x)=m,画出F(x)的图象如图3所示.
由图象看出,当m=0或m≥2时,函数F(x)与G(x)的图象只有一个交点,即原方程有一个解;当0 评注从几何直观上给出了代数形式下的新结构,因此利用数形结合的转化途径,达到了几何直观性与对数严谨性的有机统一.数形结合,沟通了数学各个分支的联系,似乎意料之外,着实情理之中,解法相当精彩. 评注优美解由函数的图象即可突破, 试题的解法于“平凡”中显“非凡”.由此可见,只要我们在学习中夯实基础,深刻领悟看似“平常”的数学概念、方法,善于进行解题反思、总结经验,所谓的高难题也就不足畏惧了.
四、多一点数形互化思考