把错因之脉 施辩证之法*──关于一道竞赛题的证明、变式及推广

●

(武功县教育局教研室，陕西 武功 712200)

在数学解题过程中,学生的思路出现问题是很正常的.在这种情况下,教师切不可轻易地放弃学生的解题思路,强制学生按照教师提供的方法来完成解题,那样做往往会阻碍学生的思维发展,甚至扼杀学生的创造性思维.因此,教师要善于从学生出现的问题中辩证地分析错因所在,做到因势利导,对症下药,这样才能清除学生的思维障碍,引领学生思维沿着正确的方向前行.

1 问题提出

题目已知a,b,c≥0，且a+b+c=1，求证：

(1)

(2007年中国女子数学奥林匹克试题第6题)

有一位学生试图利用熟知的不等式

(2)

到此,这位学生的证明失败,于是他提出了一个问题：对不等式(1),用这种方法能证明吗？

2 问题解决

在数学解题中,解题方法的确定十分重要,尤其是入手时角度的选择对整个解题起着举足轻重的作用.上面这位学生确定用不等式(2)证明不等式(1),解题方法是对的,因为从式(1)左边的结构上看确实适合用不等式(2),但问题是一开始就直接使用不等式(2)进行放缩,导致因放缩的步子过大而使证明失败.如果将放缩的步子放慢一步,那么能使问题得到解决吗？

方案1用假设法开路，借助换元，激活方程思想.

(3)

(4)

那么上述失败的证法可以修改为

从而使问题得到解决.

现在，我们来探索一下正实数p，q是否存在呢？由式(3)和式(4)，得到

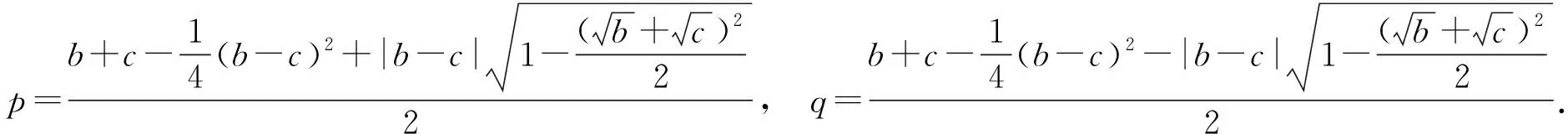
这样，我们就找到了满足条件的正实数p和q，方案1可行.

方案2从不等式入手，合理放缩，优化解决途径.

方案1虽然能解决问题，但是得到的两个正实数p和q的表达式很复杂，能否得到简化呢？

(5)

不等式(1)就可以转化为它的一个加强不等式：

(6)

下面按照方案1的思路探寻式(6)的证明.

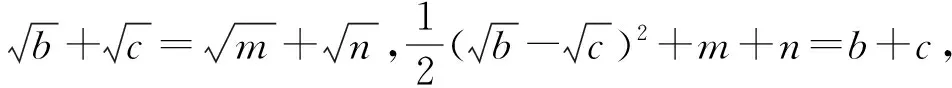
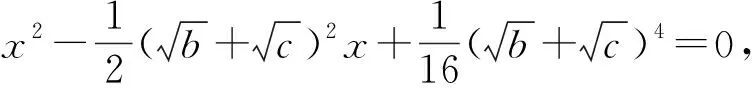
于是式(6)成立，故式(1)成立.

评注2不等式(2)是证明不等式的基本工具,但在具体应用时要灵活掌握时机,特别注意“先用”与“后用”的问题.“先用”有时会造成不等式放缩的步子过快,导致证题失效；“后用”虽然将不等式放缩的步子变慢了一些,但常常能“后发制人”,收到良好的效果.

3 问题变式

对以上证法进行反思，我们可以通过改变式(1)左边各项的内部结构，得到下面4种变式：

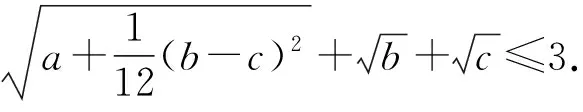
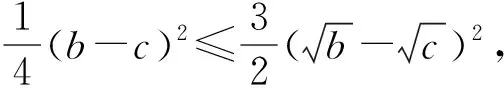
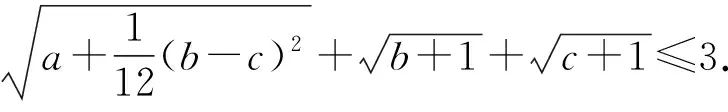
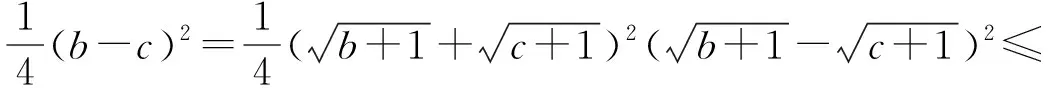
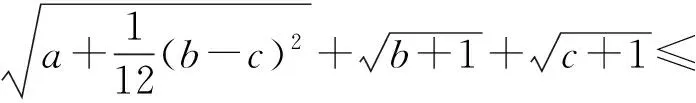
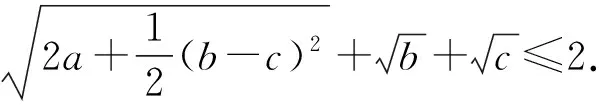
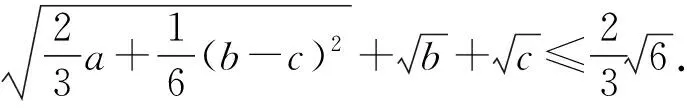
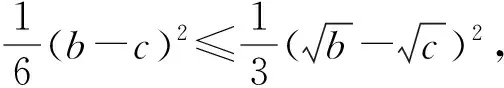
4 问题推广

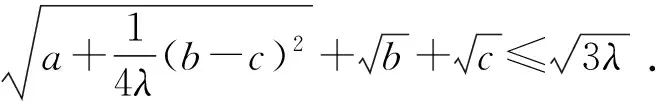
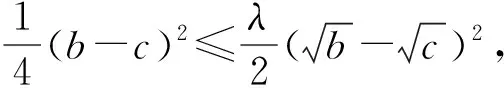
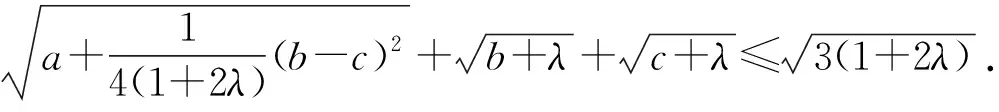
证明由于

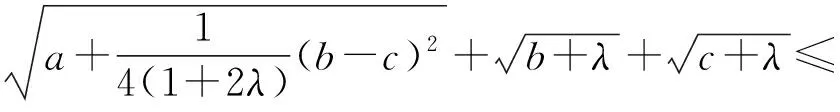
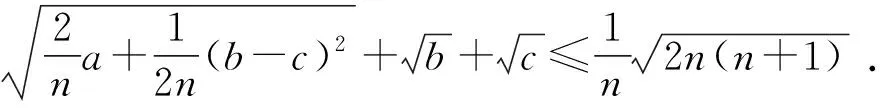
数学解题的过程是一项复杂又细致的思维工程.解题的方法和策略往往与学生掌握的知识程度、思维水平紧密相关,因为学生的基础不同,能力又有差异,所以解题中经常会出现不同的解法.在这种情况下,教师必须从学生的角度出发，帮助学生对存在的问题进行准确地把脉与诊断，有针对性地找出解决问题的突破口，这样才能从源头上彻底激活学生的思维,引领学生的数学解题能力稳步、健康地发展.