创造性挖掘教材 针对性提升素养*
——“椭圆标准方程的应用”教学札记
●
(惠安第三中学,福建 惠安 362100)
首都师范大学王尚志教授指出:教师在教学中要全面落实“立德树人”要求,深入挖掘学科的育人价值,树立以发展学生核心素养为导向的教学意识.通过教育促进学生各学科素养的发展,从整体把握学科课程,抓住学科本质,进行主题(单元)教学,以问题引领意识,为学生创设合适情境,促进学生学会学习,使学生成为全面发展的人.教师在教学实践中要结合情境不断探索和创新教学方式,有效提升学生的各学科基本能力,实现普通高中各学科的课程目标.
之于数学教学而言,其学科核心素养体现在数学运算、直观想象、逻辑推理、数学抽象、数学建模、数据处理这六大方面,这无疑为我们的日常教学定位指明了方向,也为评价课堂教学的有效性提供了参照.笔者认为:教师是落实核心素养教育体系的执行者,课堂教学是培育学科核心素养的主阵地,教材知识是提升核心素养的重要源泉(载体)[1].
下面笔者通过截取人教A版《数学(选修2-1)》教材中“椭圆及其标准方程”中的一段推导过程,创造性地给予变形拓展,充分挖掘教材知识的教育价值,引领学生一同经历数学运算处理、寻求数学模型、发挥直观想象等过程,促使学生主动参与教学活动、积极探究数学问题,从而有针对性地培育、提升学生的学科综合素养.
1 教学目标
1)由椭圆的标准方程探究椭圆的定义及性质,通过数学运算变形、发现归纳、主动探索数学问题,感受椭圆标准方程的强大功能;
2)引导学生积极参与数学运算处理,建构合理几何模型,加强知识横向联系,自然渗透数形结合、函数方程和转化化归等数学思想;
3)着力提升学生在数学运算、直观想象、数学抽象、数学建模、逻辑推理等方面的学科素养.
2 教学重点
由椭圆的标准方程探究椭圆的定义及性质.
3 教学难点
椭圆标准方程及其定义与性质的灵活运用.
4 教学过程
4.1 复习引入
4.1.1 椭圆的定义及其标准方程
|MF1|+|MF2|=2a(其中2a<|F1F2|),

设计意图复习椭圆的定义及其标准方程形式,强调椭圆定义是推导椭圆标准方程的依据,也为展开本节教学活动奠定知识根基.

图1
4.1.2 椭圆标准方程的推导
引导学生回顾阅读人教A版《数学(选修2-1)》中“椭圆及其标准方程”中的推导过程:如图1,以直线F1F2为x轴、线段F1F2的垂直平分线为y轴建立平面直角坐标系xOy.设点M(x,y)是椭圆上任一点,椭圆的焦距为2c(其中c>0),则焦点F1(-c,0),F2(c,0).由|MF1|+|MF2|=2a(其中2a>2c)得
将左边的一个根式移到右边,得
两边平方,整理得
(1)
两边再平方得
a2x2-2a2cx+a2c2+a2y2=a4-2a2cx+c2x2,
即
(a2-c2)x2+a2y2=a2(a2-c2),
亦即

设计意图鼓励学生积极参与椭圆方程的推导及生成过程,掌握数学运算、数据处理和变形优化等技巧,感受椭圆标准方程形式的简洁美与整齐美.另外,“温故而知新”,以上复习引入环节也为开展探究活动提供了素材和铺垫.
4.2 研探新知
对于椭圆的标准方程,学生往往只在乎标准方程的结果形式,忽略了其生成及推导的过程.其实椭圆的标准方程“简约不简单,平淡不平凡”,其功能强大、意义非凡.
4.2.1 椭圆的第二定义
教师引导学生观察上述推导过程中式(1)的结构特征,鼓励学生探寻其中蕴藏的几何模型及几何意义:将上述式(1)两边同时除以a,可得到
这说明求椭圆上的点到右焦点的距离可简化为关于“a-ex”的计算.类似地,上述推导过程也可变形推得
于是自然地得到椭圆的焦半径公式:
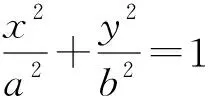
|MF1|=a+ex0, |MF2|=a-ex0.

设计意图在椭圆已有的推导过程中稍微“变动”即可自然得出焦半径公式,比两点间距离求焦半径的运算简化多了,并且也再次印证了椭圆的定义|MF1|+|MF2|=2a,这无疑让学生瞬间获得运算简捷并与定义前呼后应的喜悦感.当然也敦促学生意识到:只有真正动手参与到方程推导的具体运算中、多加反思琢磨、深入探究方可发现其中的奥妙所在.这就将学生对数学的被动运算激发为自身主动参与,数学运算素养锻炼的必要性不言而喻.
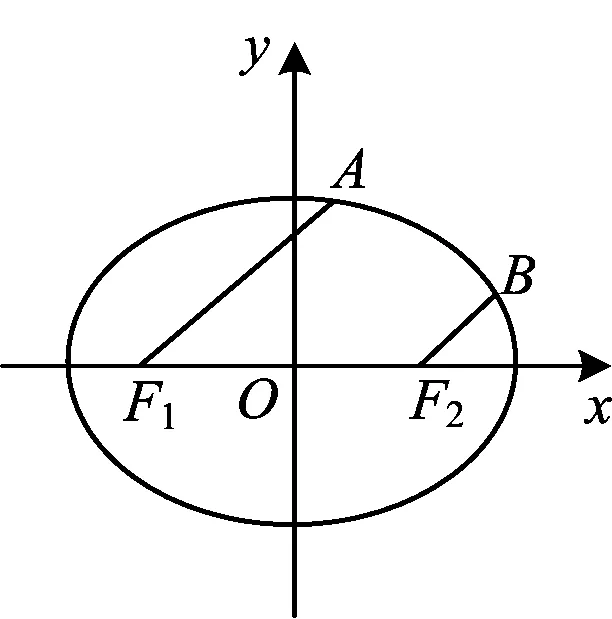
图2

(2011年浙江省数学高考理科试题第17题改编)
分析1不妨设A(x1,y1),B(x2,y2),则
依题意得

分析2不妨设A(x1,y1),B(x2,y2),则
(2)
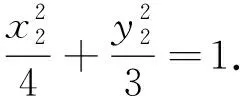
(3)

代入式(3),得
(4)
点评椭圆标准方程不仅刻画了椭圆上点的横、纵坐标之间的等量关系,也是我们进行等量代换、等价变形、消元化简的运算枢纽,还是构建几何模型、揭示几何意义的重要载体.
设计意图例1的设置旨在巩固师生刚刚探究获得的“阶段成果”,展现焦半径公式的应用功能.分析2有回归本源之功效,凸显椭圆标准方程的工具性作用,其中“点差法”蕴含着数据处理的关键技巧,其灵活简洁、优化快捷的数学运算必然带给学生无穷的魅力和浓厚的兴趣.
倘若将上述式(1)再作变形,即


图3
设计意图让学生在椭圆方程的探究中切身感悟:数学运算、变形整理是我们寻求、建立几何模型的先决基础,数据处理灵动地伴随于提炼数学模型的过程中,合理建构的数学模型有助于我们形象理解方程中的数量关系,应该说直观想象赋予了椭圆方程崭新的生命力,使得数形结合、转化化归思想在此昭然若揭.再者,我们又在椭圆特征的基础上通过数学抽象概括出其第二定义,彰显整个探究过程生动形象化与内在本质化同存并俱、交相辉映.
4.2.2 椭圆的第三定义
即
亦即

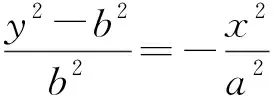
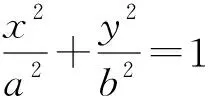
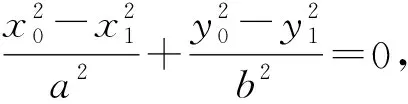
即
进而
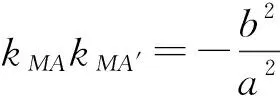
由此又可得到椭圆的第三定义:在平面内,与两个定点A,B连线的斜率之积为常数k(其中k<0且k≠-1)的点的轨迹是椭圆(不含两个定点).
设计意图继续引领学生深入探究椭圆标准方程,经过适当配凑变形,从中提炼斜率模型,师生共同归纳概括椭圆的第三定义,这就将数学运算、数学建模、数学抽象等素养的培育融合于椭圆方程的探究中.另外,距离结构、斜率结构是数量关系中最常提炼的两种模型,其也正是渗透数形结合思想、发挥直观想象的着力点.

( )
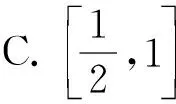
(2013年全国数学高考大纲卷理科试题第8题)
答案B.
设计意图让学生体会椭圆第三定义在全国高考中的作用与地位.
4.2.3 椭圆中点弦的性质
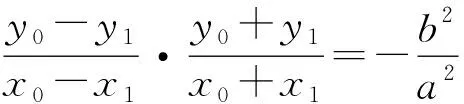

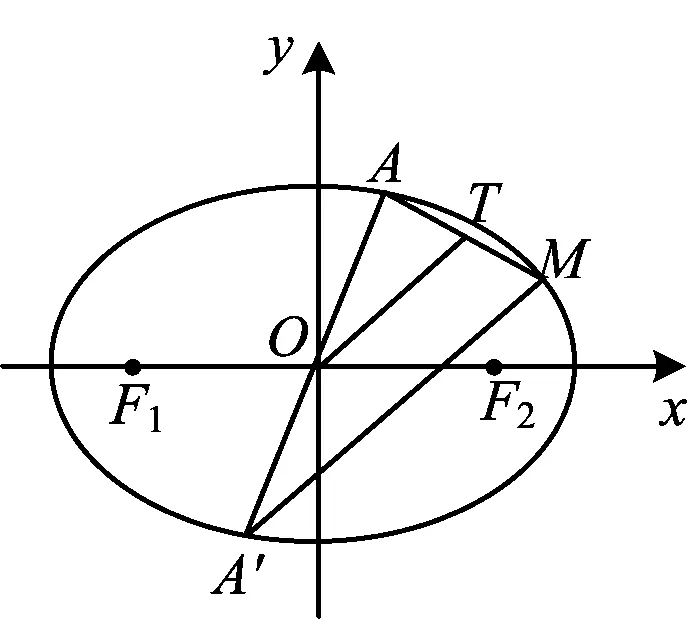
图4
如图4,OT是△AA′M的中位线,则OT∥A′M,从而
设计意图展现“点差法”是椭圆方程发挥功能的常规渠道,通过不同视角的探究,给予了椭圆方程丰富的内涵,椭圆弦的性质特征与其第三定义一脉相承、彼此交融.


即
3x-4y-7=0.

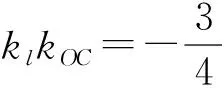
推论1椭圆一组平行弦的中点同在一条过中心的直线上.
设计意图让抽象的探究结论在具体事例中得以形象、简捷地应用,夯基固本、学以致用.另外,在题目变式设置中,倡导问题求解和问题探究并肩同行、相辅相成,这有利于促进学生养成学会思考、主动探究、深入钻研的良好习惯.
4.3 课堂总结
1)课堂活动的主线是:
椭圆定义1(初始定义)⟹椭圆的标准方程⟹

2)椭圆标准方程“简约不简单,平淡不平凡”.
①运算变形、配凑整理是探索方程、发挥方程功能的基础和支撑;
②方程中蕴含的几何特征赋予了方程崭新的生命力,也是实现数形结合的着力点;
③椭圆定义与方程一脉相承、彼此交融,椭圆是定义的“化身”,方程是椭圆的“结晶”.
3)本节椭圆方程问题的探究有助于我们提升在数学运算、直观想象、数学抽象、数据处理、逻辑推理、数学建模等方面的学科素养.
4.4 作业布置(略)
5 评价反思
本节课内容源于教材,但又不拘泥于教材.通过对椭圆方程生成之前和生成之后的变式探究,巧妙地将椭圆的初始定义、第二定义、第三定义和弦的性质等有机地融为一体.整节课线索分明,系统高效、淋漓尽致地揭示了椭圆定义、方程以及几何性质之间的来龙去脉和内部联系,其中运算变形、数据处理、数形结合等得到了恰如其分的展现,椭圆标准方程自始至终闪耀着其光芒四射的强大功能,也散发着其灵巧奇妙的独特魅力.
本节课旨在敦促学生自觉主动地参与运算变形、构建模型、应用结论等探究活动,有针对性地提升学生在数学运算、数据处理、数学建模等方面的学科素养.另外教师通过引导学生参与猜想发现、数形结合、归纳概括等一系列过程,也可实质性地培育学生直观想象、逻辑推理、数学抽象等方面的核心素养.应该说,整个课堂活动结构新颖、设计严谨、目标明确、线条清晰,创新务实地以知识为载体,展现知识价值,注重能力立意,突出数学素养.
因此,在落实“立德树人”根本任务、全面提升核心素养的教育形势下,数学教师在课堂教学中要紧密联系教学实际,充分发挥教材知识的教育价值,创设合理的问题情境或探索路径,鼓励学生广泛参与各种探索活动,提高学生运用知识解决实际问题的能力,让学生在实践探索中加深对数学知识的理解感悟,感受到数学学习的乐趣和应用价值,真正促进学生的个性发展和核心素养的有效提升[2].这也就要求我们数学教师:要以教师的问题创设去激发学生的学科兴趣,要以教师的深入研究去引领学生的主动探究,要以教师的良好涵养去培育学生的核心素养.

