从几何意义角度解决几类距离问题*
●
(丽水中学,浙江 丽水 323000)
一份高质量的数学试卷往往都配有高质量的“小题”,这些小题很多时候都以简洁美呈现.教师在平时讲解过程中也一直强调要洞察题目的背景,但是学生实践起来却没有那么顺利.追其究竟,其实是学生没有看透问题的本质,被题目的外表所迷惑.本文从几何意义角度对距离问题的几种形式进行探究.学生在初中阶段学习过数轴上两个点的距离公式,高中阶段学习过两点间距离公式和点到直线的距离公式,这两类问题通过转化都可以用距离的几何意义去解决.正如法国数学家姬曼所说:代数不过是书写的几何,而几何不过是图形的代数.
1 类型呈现
类型1d=|x-x0|.
例1已知f(x)=|x+1|+2|x-a|的最小值是5,则实数a=______.
分析f(x)可以看成是数轴上一个动点到-1的距离和到a的距离的两倍之和.当x=a时,f(x)取到最小值|a+1|=5,故a=-6或a=4.
点评用数轴上点的距离去处理这个问题比分类讨论简单易懂,学生也容易掌握.

( )
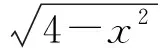
分析|x-1|是圆x2+y2=4上一动点P(x,y)到定点(1,0)横坐标之间的距离,则
|x-1|≤|x|+1.

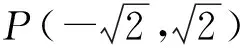


例2设x,y∈R,则(3-4y-cosx)2+(4+3y+sinx)2的最小值为______.

点评式子结构与两点间距离公式一致,只不过点都是在变化的,找到动点满足的轨迹分别是直线和圆,问题就转化为直线上的点与圆上点的距离最小值的平方,那么所求就是圆心到直线的距离减掉半径的平方.

( )

点评首先题目的条件有两个变量,结构是平方和,如果把平方乘开,处理起来比较麻烦.如果想到这个模型就是两个动点之间的距离,那么分别找到动点所满足的曲线方程,用数形结合去解题就可以化难为易.
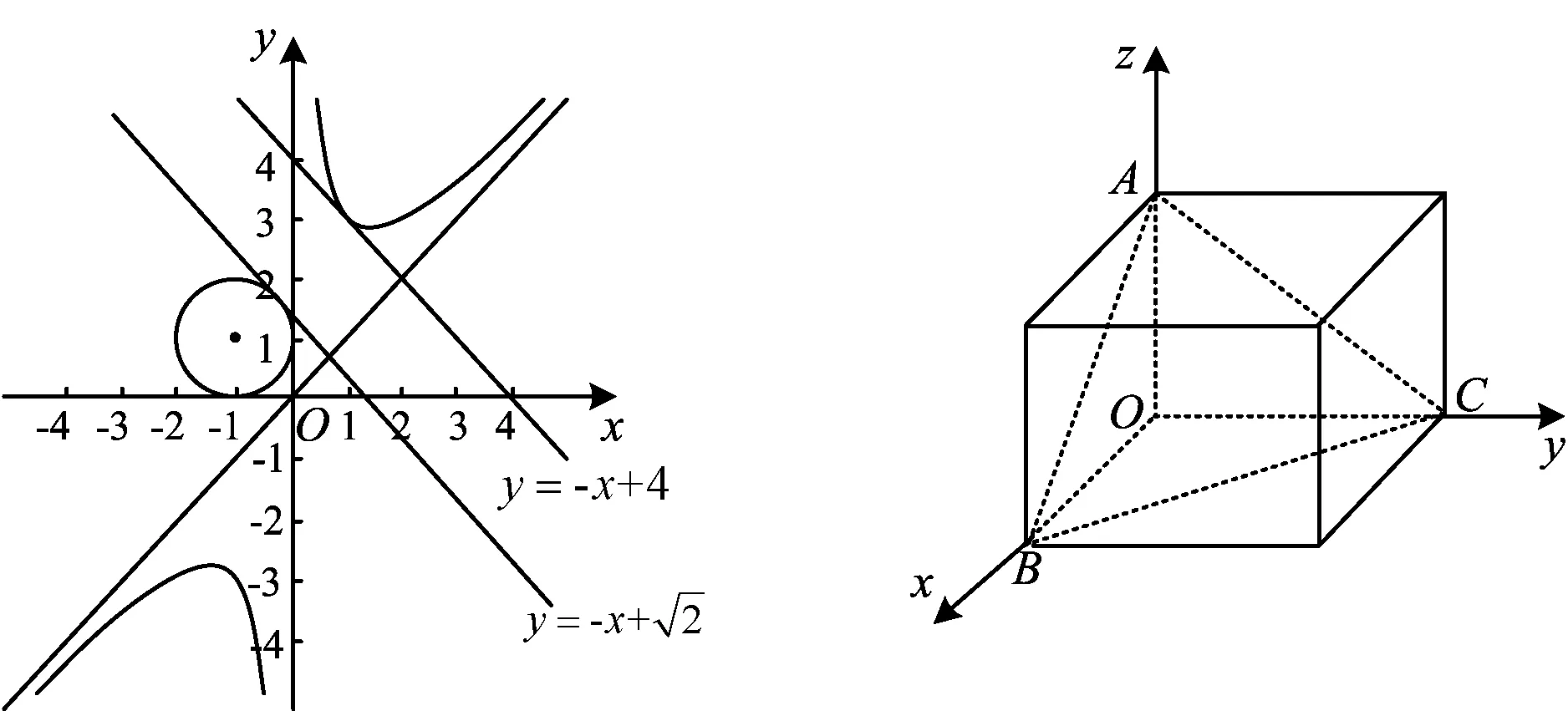
图1 图2
变式2已知x,y均为非负实数,且x+y≤1,则4x2+4y2+(1-x-y)2的取值范围是______.
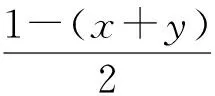
|OP|2=x2+y2+z2,
于是原问题转化为求|OP|的取值范围.显然|OP|≤1,且|OP|的最小值为O到平面ABC的距离.利用等积法计算:因为VO-ABC=VA-OBC,得
所以
即
点评将题目的条件和目标联系起来是双元不等式问题,通过不等式放缩或者柯西不等式可以得到答案,但处理起来比较麻烦.经过合理换元后目标式的结构就与空间距离一致,利用空间距离的几何意义就能很巧妙地解出了题目.

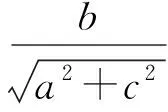
( )
航摄操作开始前,在主控计算机内输入所有相片曝光点位置以及航摄航线具体信息。航摄过程中,姿态测量系统的GPS接收机以2Hz的频率对双GPS天线做实时定位,同时,双GPS天线位置对飞机的偏航程度做出计算。姿态测量系统检测飞机位置已到达设计曝光点时,航摄控制器发出开启相机快门的指令从而控制航摄仪的曝光,同时完成相机曝光脉冲信号的写入操作,写入于定位GPS接收机时标上,以保证所有像片曝光的精度[2]。
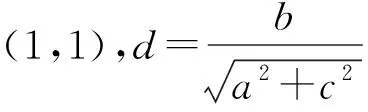
由a>b,知a>-a-c,从而
同理可知
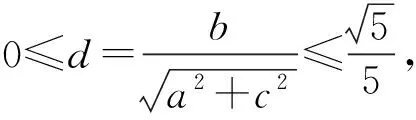
点评例3处理的办法比较多,可以用特殊值、均值代换、消元等,但是目标式的结构与点到直线的距离结构是一致的,难点在于条件中没有现成的直线.巧妇难为无米之炊,需要对条件式进行构造,构造出一条过定点的直线,这是本题的点睛之笔.
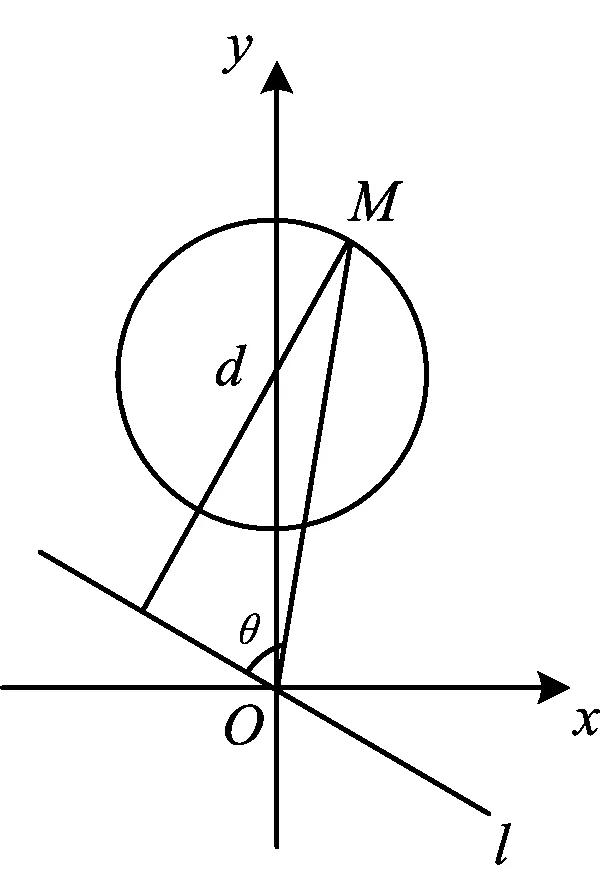
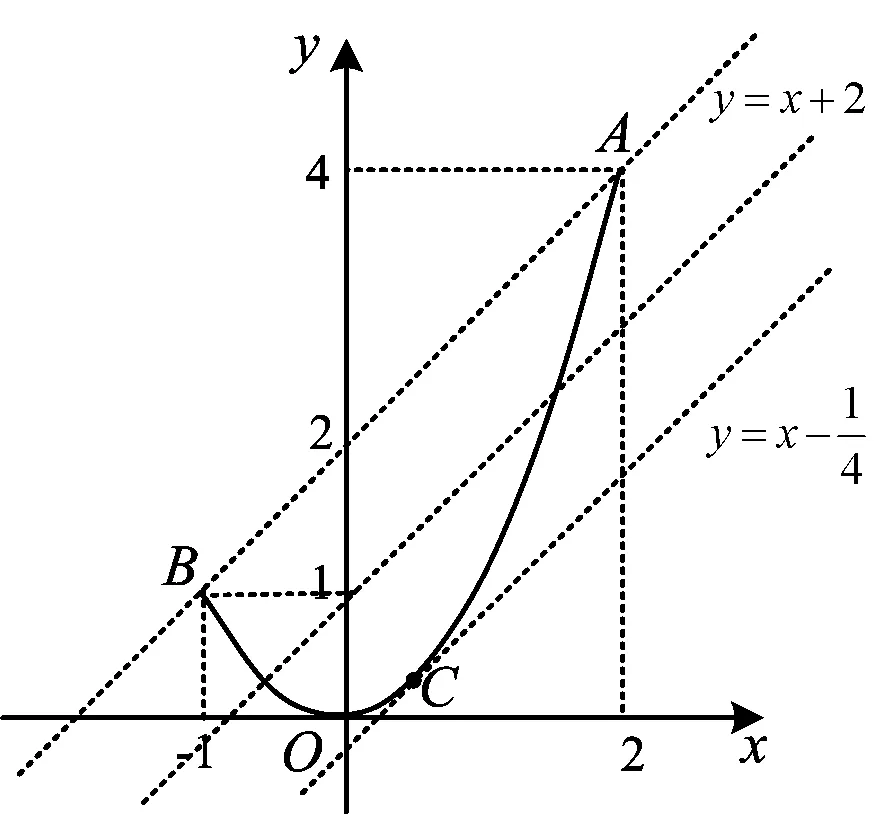
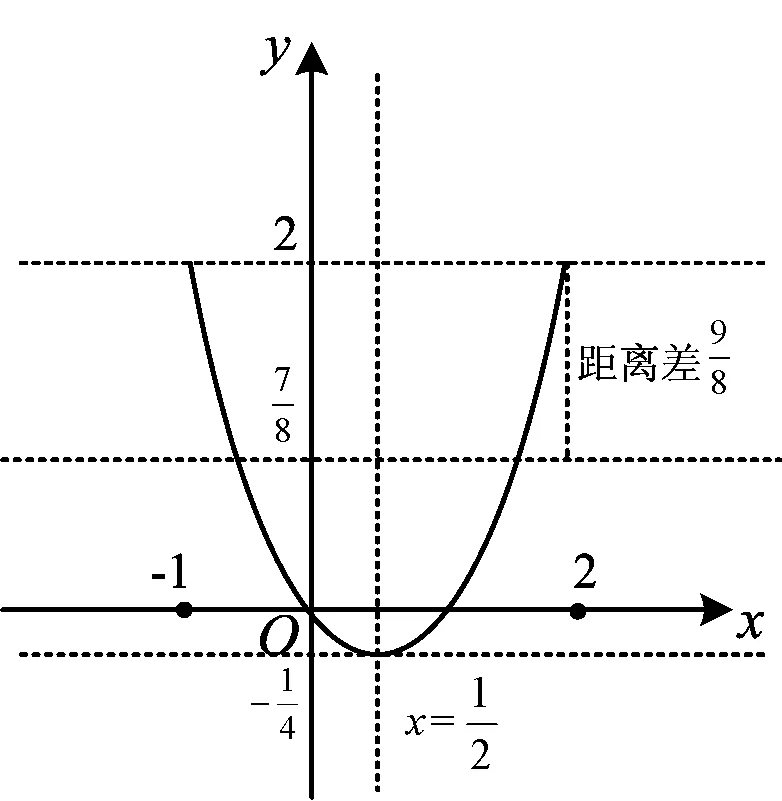
变式1已知实数a,b,c满足a2+b2≤c(其中0 分析设动点P(a,b)满足直线方程z=a+b,由a2+b2≤c(其中0 从而 点评题目本身没有显而易见的距离结构,条件与目标经过合理的代换就具备了距离的几何意义.借助几何意义实现了整体消元,过程简洁,化繁为简,体现了转化与化归思想在数学中的重要意义. ( ) 图3 点评构造出点到直线的距离,借助数形结合思想,从图形直观上去破解问题,计算量小,过程简洁[1]. 类型4d=|h(x)-g(x)|. 例4f(x)=|x2-ax-b|(其中x∈[-1,2])的最大值为M(a,b),对任意a,b∈R,求M(a,b)的最小值. 图4 分析f(x)为h(x)=x2与g(x)=ax+b纵坐标之间的距离.因为a,b∈R,在直线旋转的过程中,发现M(a,b)的最小值取到的位置如图4所示: 1)联结两个端点(-1,1),(2,4),作直线l1:y=x+2; 图5 (2018年浙江省高中数学联赛试题第12题) 分析设h(x)=x2,g(x)=-ax-b,当g(x)分别经过点(0,0),(1,1)时,-b分别为0和1+a,于是|1+a-0|≥2,得a≥1或a≤-3(如图7和图8),经检验成立. 图7 图8 高中数学以“距离”为背景命制的小题有很多,有些一目了然,有些却隐藏得很深,我们需要练就火眼金睛去发现并解决那些深藏的距离问题.如果没发现距离的几何意义,解决此类问题就会遇到繁琐的运算.数学的解题离不开运算,但是数学的解题不止考查运算,他还是数学建模、逻辑推理、数形结合等思想的结合,多想一点题目命制的背景,以形助数,把握数形之间的内在联系,真正做到小题小做.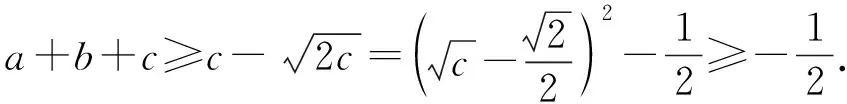
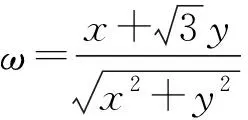

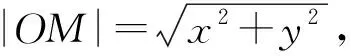
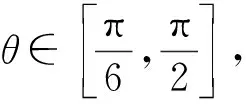
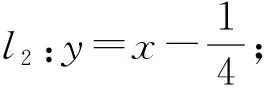
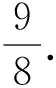


2 一点感悟

