生遇困境独难支 微专助力信心升*
——一类含绝对值二次型函数微专题的开发和实践
●
(宁波市第二中学,浙江 宁波 315010)
1 专题背景
2019届高三一轮复习大幕已经拉开,各校都进入了紧张有序的复习模式.笔者所在学校于8月下旬开始函数一轮复习,在复习完二次函数和幂函数一节后布置《2019届数学全品一轮》课时作业(七)作为课后作业.第二天笔者在批改作业时发现最后一题基本上没有学生做对,很多学生都以空白形式呈现.为了方便说明,现将问题摘录如下:
例1设f(x)=2x2+(x-2a)|x-a|,若f(x)在[-2,1]上不是单调函数,则实数a的取值范围是______.
(《2019届数学全品一轮》第13页第16题)
2 学情分析
2.1 学生已有认知
会求二次函数在闭区间上的最值,会去绝对值将原函数化为分段函数.
2.2 学生思维障碍
缺少画出f(x)图像的意识,对图像在分界点处的形态不清晰,找不到分类讨论的标准,不会讨论或讨论不全.
3 教学目标
1)能熟练画出此类含绝对值二次型函数的图像;
2)会对二次函数对称轴和界点及区间端点进行分类讨论;
3)对已知最值尽可能先缩小参数范围,从而简化或避免讨论.
4 教学设计
元认知是20世纪70年代由弗拉维尔提出的概念,就是个体关于自己的认知过程的知识和调节这些过程的能力.元认知策略是基于学生对自己的认知过程及结果的有效监视及控制的策略,包括计划策略、监控策略和调节策略.
基于对元认知策略的认识及学生学情和教学目标,我们将此块内容设计成如下微专题.
微专题片段1
例2设f(x)=2x2+(x-2a)|x-a|.
1)求f(x)的最小值;
2)若f(x)在[-2,1]上不是单调函数,求实数a的取值范围.
(《2019届数学全品一轮》第13页第16题改编)
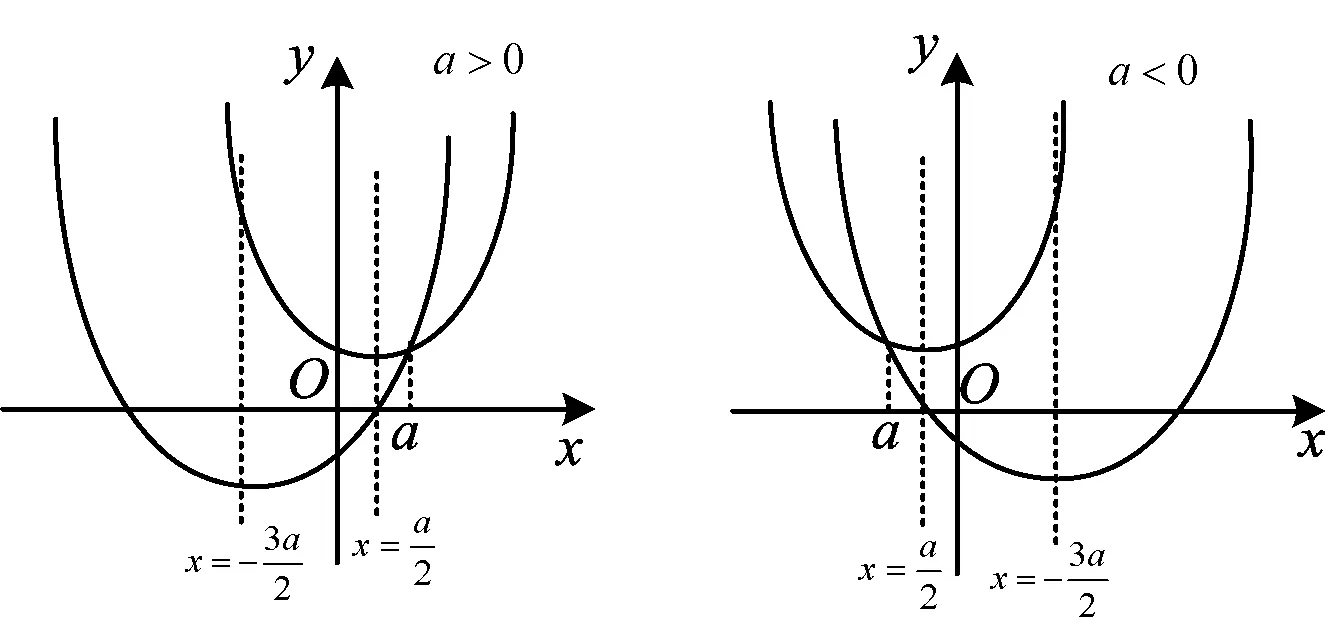
图1
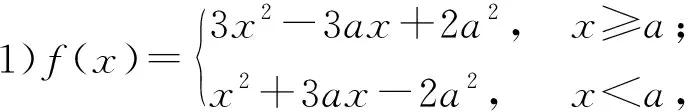
画出函数图像如图1所示,则
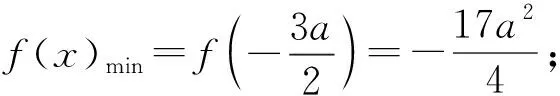

当a=0时,f(x)min=0.

2)由图像可得
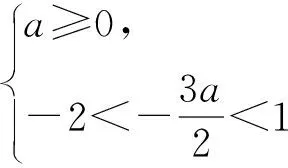
从而
例3设函数f(x)=x2+|x-a|+1,其中x∈R,求函数f(x)的最小值.

图2
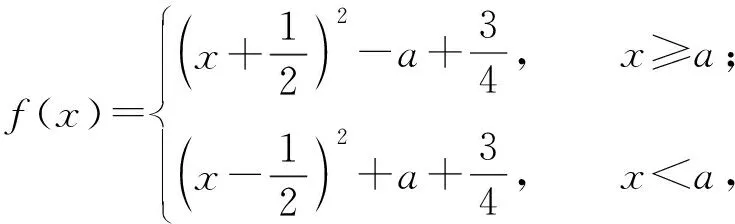
画出函数图像如图2所示,则
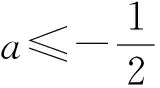
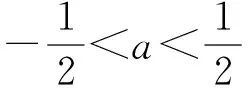

例4已知函数f(x)=x2+(x-1)|x-a|,若不等式f(x)≥2x-3对一切实数x∈R恒成立,求a的取值范围.

图3
解设
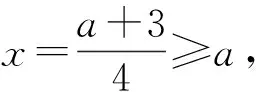
于是
-3≤a≤5.
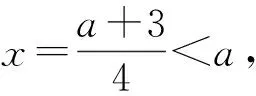
设计意图最值是函数的一个重要性质,例2增加第1)小题旨在回顾求函数(特别是分段函数)最值的方法,引导学生利用图像法求解;通过此小题的求解,适时总结画图的具体步骤,同时为第2)小题的顺利解决奠定基础.例3是认知计划的即时应用,适当增加了分段的类型,考查学生认知的自我监控和调节策略,即发现问题及时采取不同分类讨论的情形.通过例4强化认知监控策略,即根据函数目标的构造反馈认知活动中的结果和不足,同时依据解题的有效性评价函数构造的效果,并进一步强化方法的灵活应用.
微专题片段2
例5设f(x)=2x2+(x-2a)|x-a|.
1)求f(x)的最小值;
2)求f(x)在[-1,1]上的最小值.
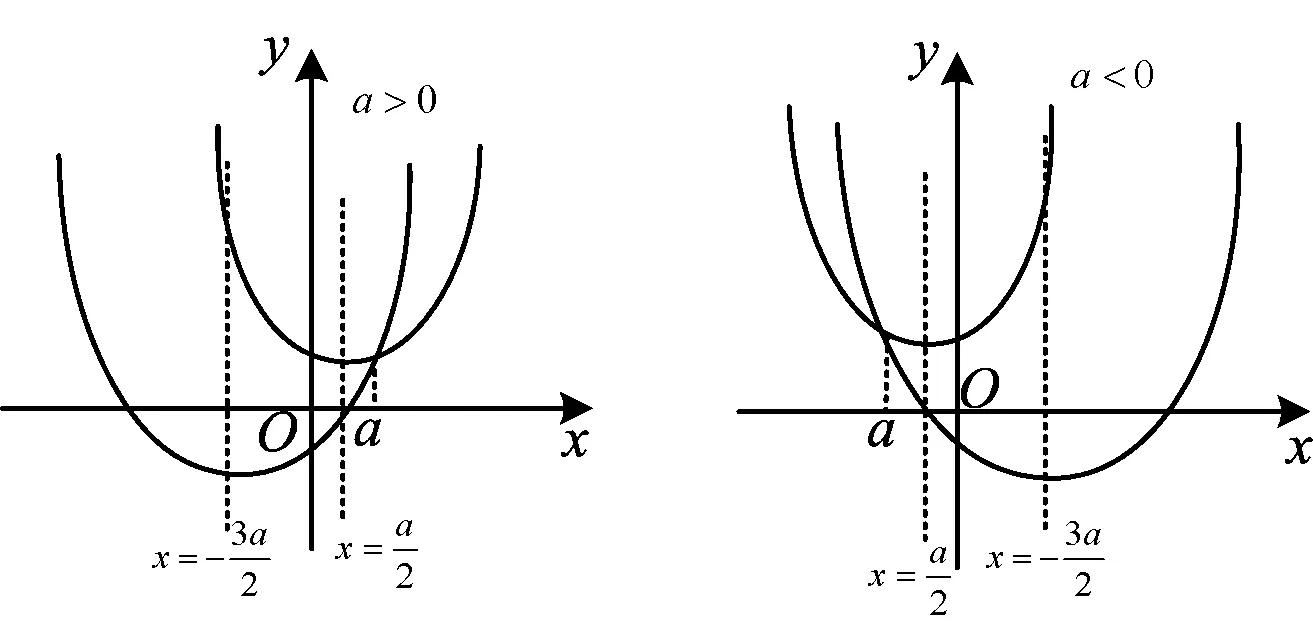
图4
1)同例2第1)小题(略).
2)解如图4,根据对称轴位置(极值点)与区间左端点-1展开讨论,易得:
当a≤-2时,f(x)在[-1,1]上单调递增,故
f(x)min=f(-1)=-2a2-a+3;
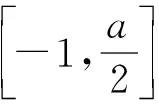
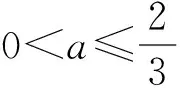
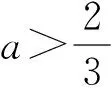
f(x)min=f(-1)=-2a2-3a+1.
例6[1]设a∈R,求函数f(x)=x|x-a|在[-2,2]上的最大值.
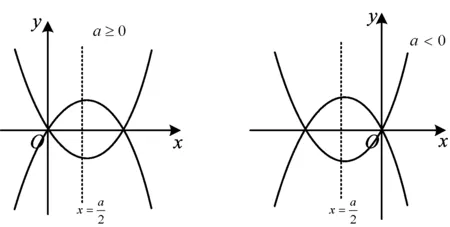
图5
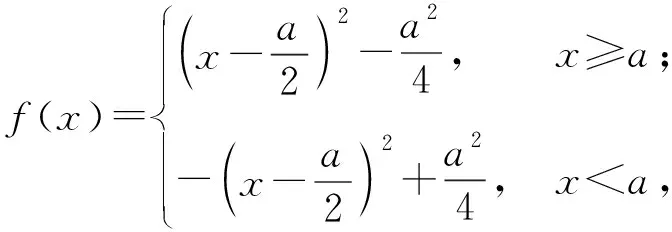
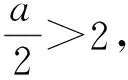
f(x)max=f(2)=2a-4;
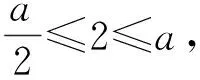
若0 当a≤0时, f(x)max=f(2)=4-2a. 例7已知t为常数,函数y=|x2-2x-t|在区间[0,3]上的最大值为2,则t=______. (2008年浙江省数学高考理科试题第15题) 解法1设f(x)=|x2-2x-t|,当Δ≤0,即t≤-1时, f(x)max=f(3)=2, 不合题意; 当Δ>0,即t>-1时, f(x)max= max{f(1),f(3)}= max{|-1-t|,|3-t|}=2, 得 t=1. 解法2由图形易得 f(x)max= max{f(1),f(3)}= max{|-1-t|,|3-t|}=2, 得 t=1. 解法3设m=x2-2x∈[-1,3],则 y=|m-t|, 从而 ymax=max{|-1-t|,|3-t|}=2, 得 t=1. 例8已知a>0,函数f(x)=|x2+|x-a|-3|在[-1,1]上的最大值为2,则a=______. (2017年浙江省绍兴市数学适应性考试第17题) 解由f(0)≤2,得||a|-3|≤2,从而 1≤|a|≤5(其中a>0), 于是 1≤a≤5, 此时 f(x)=|x2-x+a-3|, 故 设计意图通过例5的第1)小题再次巩固已有的认知水平,第2)小题通过引入区间增加分类讨论的类型,此时仅考虑对称轴(极值点)与一个端点的位置即可,不必考虑端点和分界点的大小.由此总结画图的基本步骤是先去绝对值化为分段函数,明确图像在分界点连续情况的基础上展开分类讨论,即对对称轴(极值点)、分界点以及区间端点进行大小讨论.具体操作是先对极值点和分界点大小展开第一次分类讨论,即先画对称轴,再标分界点截取图像,之后再对区间位置展开第二次分类讨论.例6通过改变最值类型加大分类讨论的难度,进一步强化认知监控策略和调节策略.例7引入高考真题以检验学生的解题能力,问题类型有别但解题方法相同.例8渗透小题小做的解题策略,由必要性先缩小a的范围从而去掉绝对值,避免了分类讨论,大大提高了解题效率. 通过微专题片段1的教学,学生基本掌握了含绝对值二次型函数的图像特点,作业整体效果较好,达到课前的教学目标.基础较差的学生也能较好掌握这类函数在定义域R上的画图步骤,能有意识地利用图像解决相关的函数问题.通过微专题片段2的教学,学生进一步了解了一般分类讨论的标准,即极值点、分界点及区间端点大小讨论,通过程序化的操作步骤降低了分类讨论的难度. 笔者在微专题课堂教学后与学生的访谈中发现:学生对微专题的教学形式表示欢迎和认可,理由是通过微专题学习让其对一类问题有了通法上的感受和领悟,从原来对这类函数问题心存畏惧到内心上不害怕,解题策略上有章法,极大地提高了解题的自信心和期望值.但少部分基础薄弱的学生仍然存在着讨论的盲目性,需要进一步强化方法的梳理和理解. 高考复习的目标其一是帮助学生构建有序和完善的知识结构,提炼方法体系;其二是演练高考(模拟)试题,提高应战能力;其三是暴露教与学问题以及时调整复习策略.通过及时发现问题、搜集相关微专题素材进行专题突破应是高考复习中的必要手段.教师要具有善于发现和整合教学资源的能力,根据学生的学情和考情等及时开发微专题,灵活适度地穿插于不同的教学情境之中.学生存在的知识盲点与易错点、某种类型中方法能力的薄弱点、疑难问题中的困惑点和学生素养培育中的思维拐点都是微专题生成的“再生资源”[2]. 微专题作为一种小切口教学方法具有微而灵活、微而知著和微而深入等特点,以“小专题、大视野”的格局来优化课堂教学,正是由于微专题小巧灵活、主题鲜明,属于学生的个性化“私人订制”,我们有理由相信这样的专题教学是深入和高效的,是学生“最近发展区”的深入延展,更是学生思维品质不断优化的重要抓手.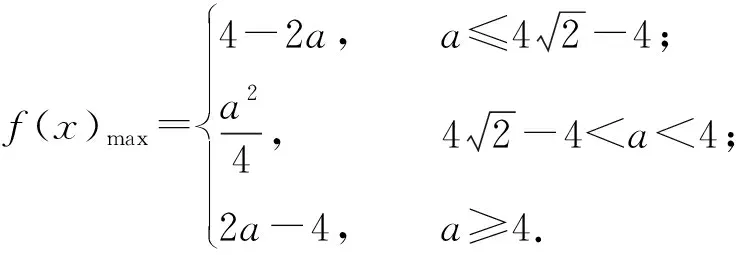


5 教学效果
6 教学反思

