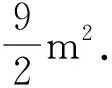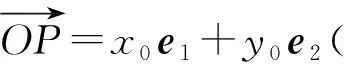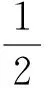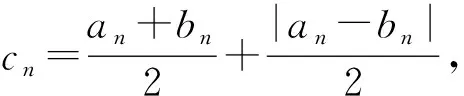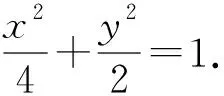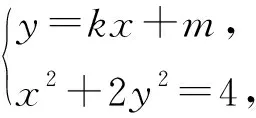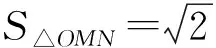抓住关键“点” 顿悟其中玄*
●
(池州市第一中学,安徽 池州 247000)
数学问题中,常常有一些关键的“点”,比如原点、端点、中点、零点、定点、焦点、切点、拐点、间断点、中心点、对称点等等,这些点往往是我们求解问题的“制高点”“切入点”“着眼点”“着力点”“落脚点”“平衡点”“易错点”“突破点”,虽然只是一个“点”,但其作用不可小看,对整个问题的求解起到了核心关卡作用,牵一发而动全身.如果能善于发现这些“点”,用好这些“点”,就能顿悟其中隐含的玄机,迅速找到解决问题的突破口,把握求解方向,顺流直下,顺势而为,势如破竹,问题轻松求解,从中感悟到方法美、思想美、简单美,美不胜收.
1 抓住关键“点”,把持“制高点”
有些关键“点”好比“制高点”,有“一夫当关万夫莫开”之势,也好比“华山自古一条道”.也就是说,如果没有抓住这个“点”,那么问题就很可能无法求解,就会思路出错,思维偏差,就会产生错误的解法.如果抓住了这个“点”,也就把持了问题求解的“制高点”,就能打通关卡,问题求解也就势如破竹,迎刃而解.
例1已知函数f(x)为定义在R上的奇函数,当x≥0时,f(x)=x2+2x+mcosx,记a=-3f(-3),b=-2f(-2),c=4f(4),则a,b,c的大小关系为
( )
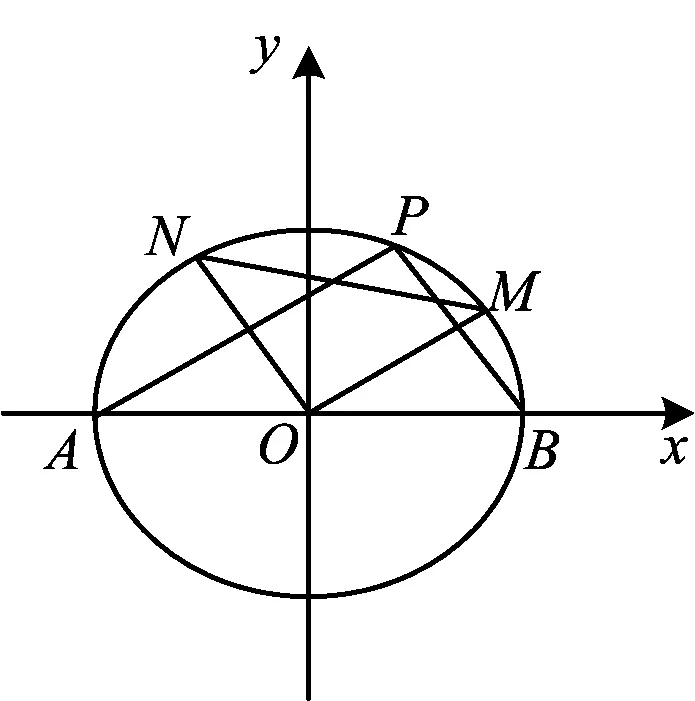
A.b C.c 解因为f(x)为定义在R上的奇函数,所以 f(0)=0, 从而 m=0,f(x)=x2+2x(其中x≥0). 易知 a=3f(3),b=2f(2), 令 g(x)=xf(x)=x3+2x2(其中x≥0), 则 g′(x)=3x2+4x≥0(其中x≥0), 从而函数g(x)在区间(0,+∞)内单调递增,又a=g(3),b=g(2),c=g(4),于是b 评注这是一道高三模拟考试题.不少学生由于没有抓住“奇函数在原点有定义时f(0)=0”,也就不能求出m=0,结果问题求解陷入困境.本题中的坐标“原点”是关键“点”,是问题求解的“制高点”,它直接控制着本题的进展,只有把持住这个“制高点”,这道题才能顺利求解. 例2已知函数f(x)=ax2+bx+3a+b为偶函数,定义域是[a-1,2a],求f(x)的值域. 解因为函数f(x)=ax2+bx+3a+b为偶函数,所以定义域关于原点对称,即 2a=-(a-1), 评注绝大部分学生都能求出b的值,但没有想到偶函数的定义域关于原点对称,并利用这一重要条件求出a的值.大部分学生求解这道题时分a>0,a=0,a<0这3种情况讨论,使问题求解走入误区.可见这里区间的“端点”是本题能够顺利求解的“制高点”. 有些关键“点”是问题求解的“切入点”,这些“点”往往比较隐含,不容易被发现,需要我们有较强的探究能力,把这些“点”挖掘出来并加以利用,就能使问题顺利求解. 例3已知函数f(x)=(2x2-a2x-a)lgx的值域是[0,+∞),求a的值. 解令g(x)=2x2-a2x-a,h(x)=lgx,已知函数f(x)=g(x)·h(x)的值域是[0,+∞),当x>1时,h(x)>0,g(x)>0;又当0 g(1)=2-a2-a=0, 得 a=-2或a=1, 经检验知a=1符合题意,故a=1. 评注函数的值域是所有函数值的集合.本题中函数f(x)的值域是[0,+∞),即对任意x>0,有 f(x)=g(x)·h(x)≥0, 即g(x)与h(x)同号.因为h(1)=0,又g(x)为二次函数,抛物线开口向上,所以g(1)=0,从而求出a的值.本题中的“分界点”x=1是问题求解的“切入点”. 例4已知函数f(x)=lg (ax-kbx)(其中a>0,b>0,k>0)的定义域是(0,+∞),是否存在这样的a,b,使f(x)恰在(1,+∞)上取正值,且f(2)=lg 5?若存在,求出a,b的值;若不存在,请说明理由. 解因为函数f(x)=lg(ax-kbx)(其中a>0,b>0,k>0)的定义域是(0,+∞),所以 a0-kb0=0, 即 k=1, 从而f(x)=lg (ax-bx)(其中a>0,b>0). 又f(x)恰在(1,+∞)上取正值,得f(1)=0,即 lg (a-b)=0, 从而 a-b=1. 又f(2)=lg 5,即 lg(a2-b2)=lg 5, 得 a2-b2=5, 从而 a=3,b=2. 评注函数的定义域是所有自变量取值的集合.x=0是方程ax-kbx=0的解,从而k=1,又f(x)恰在(1,+∞)上取正值,于是f(1)=0,得出a-b=1.本题中有两个“分界点”x=0和x=1都是问题求解的“切入点”. 看准“着眼点”,就是眼光要重点盯在哪里、落在何处,从哪里开始顺藤摸瓜、抽丝剥茧、分析判断,最后快速形成解题方案,再精准出击.看准“着眼点”,需要我们有一双“慧眼”来发现和捕捉,更需要有一种思维意识和较深的数学功底,这样才能将“着眼点”看得更准. ( ) 图1 即 则 从而 有些关键“点”是问题求解的“着力点”,也就是问题求解能够“着力”的“点”.这些“着力点”往往隐含在题设条件中,需要我们有一双“火眼金睛”来发现和捕捉,更需要培养思维意识,这样才能发现这些关键“点”,感悟这些“点”的价值和作用. 例6已知f(x)=ax2+bx+c(其中a>0),2a+3b+6c=0,求证:f(x)在(0,1)上有零点. 又 f(0)+f(1)=c+a+b+c=a+b+2c= 有些关键“点”是问题求解的“落脚点”,是解决问题的重点所在、重心所在.解决这类问题时要形成条件反射,首先要想到求这些“点”,然后把其他条件都转化到这个“落脚点”上来,再立足这个“落脚点”,就能使问题顺利求解. 例7当0 解易知直线l1,l2均过定点A(2,2),l1与y轴的交点为B(0,2-a),l2与x轴的交点为C(a2+2,0),所围成的四边形即为OBAC.设四边形OBAC的面积为S,则 S=S△OAB+S△OAC= 评注直线l1与l2均为动直线,但我们容易发现它们均经过定点A(2,2),抓住了这个定点,就掌握了解决这类问题的“关键技术”.以“定”解“动”是求解这类问题的重要方法和策略,求出的“定点”是解决这类问题的“落脚点”. (|PF1|+2)-(|PF2|-1)= |PF1|-|PF2|+3= 6+3=9. 有些关键“点”是问题求解的“平衡点”,考虑式子或图像具有某种对称性,根据这种对称性,探寻图像或两点的“平衡点”,然后巧用这个“平衡点”,就能使问题求解变得简单而美妙. 例9已知α是函数f(x)=xlogax-2 018的一个零点,β是函数g(x)=xax-2 018的一个零点,求α·β的值. 解由f(x)=0得 由g(x)=0得 得 α·β=2 018. 评注将函数问题转化为方程问题,再将方程变形为具有某种对称意义的形式,利用互为反函数图像的对称性得出两个关键“点”A,B,再求出AB的中点M,利用点M在直线上,使问题巧妙求解,这里的对称点A,B及中点M都是“平衡点”. 有些关键“点”是问题求解的“易错点”.由于某些条件比较隐含,易被忽视,往往成为问题求解的“易错点”.如果我们对这些“点”能高度重视,形成条件反射,就能增强思维的严密性和批判性,从而有效地谨防“易错点”. ( ) A.3 B.5 C.7 D.9 f(0)=0,f(-1)=-f(1)=0, 进而可得f(2)=f(3)=f(4)=f(5)=f(6)=0,于是函数f(x)在区间[0,6]上的零点个数是7.故选C. 即 从而 进而可得 评注本题的错解是审题不仔细造成的,对于关键的信息(区间的“端点”)审视不透,没有洞察其中隐含的玄机,考虑问题不深刻、不全面,思维有漏洞.这里区间的“端点”是学生求解的“易错点”. 有些关键“点”是问题求解的“突破点”,对整个问题能否巧妙求解起到了至关重要的作用.如果能够发现这个点隐含的玄机,就能把准突破口,找到简洁思路,使问题的求解按照预定的程序顺利进行,更加胸有成竹. 不合题意. a2x+(2a-1)≥0, 即 2a-1≥0, 评注解法1是常规解法,过程有些复杂,关键是分类标准怎么想到,这对大多数学生来说还是比较困难的.解法2是根据区间端点函数值的特殊性:f(0)=0,得出f(x)在x=0的右侧必须呈现上升的趋势,从而f′(0)≥0,这种解法就是利用区间端点这个关键“点”作为“突破点”,首先锁定参数的范围,再验证这个范围的正确性,这种解法就简单多了,而且便于操作. 评注“抓住本质,回归定义”是我们解决这类问题的有效策略.定义、定理、公式和法则是解题的依据,当学生学习了定理、公式和法则之后,容易忽视利用定义进行解题.其实,回归本源是目前高考、学考的热点所在.类似的高考题,如2018年浙江省数学高考理科试题第8题、2018年11月浙江省数学学考试题第18题等. 所谓定义型信息题是指通过定义揭示事物的一类本质特征、人为地解释意义的一类问题.常见有定义新概念、定义新运算、定义新性质等类型,主要考查学生对新定义的理解、应用与转化的能力. 例2设数列{an}的前n项和为Sn,若存在实数M>0,使得对任意的n∈N*,都有|Sn| ( ) A.若{an}是等差数列,且首项a1=0,则数列{an}是“L数列” B.若{an}是等差数列,且公差d=0,则数列{an}是“L数列” C.若{an}是等比数列,且公比q满足|q|<1,则数列{an}是“L数列” D.若{an}是等比数列,也是“L数列”,则数列{an}的公比q满足|q|<1 分析本题是定义新概念型问题.阅读本题定义的符号语言、文字语言,发现数列{an}为“L数列”,就是-M 评注“读懂定义,转化问题”是解决定义型信息题的思维策略.对于新定义,首先理解题意,要做到:1)字面理解要求读懂其中每一个句子的含义;2)深层理解要求深入理解新的概念的本质属性,分清新定义条件和结论,找到突破问题的关键等.然后转化问题,通过对新定义信息的加工、改编处理,转化为我们熟悉的数学语言、数学概念、数学图形等.最后,解决问题.类似的高考题,如2016年全国数学高考卷Ⅲ理科试题第12题、2016年浙江省数学高考理科试题第18题等. 开放型研究题是指一些不能那么轻易地只用一个简单的“是”“不是”或者其他一个简单的词、数字来回答的问题,与我们常见的数学封闭式问题相对.开放式问题可分为条件开放、问题开放、结论开放、综合开放、策略开放等,常见的问题如在特定情境下命题的条件、结论不确定的开放型试题. 例3在△ABC中,角A,B,C对应边a,b,c,若a2=b2+c2,则△ABC是直角三角形.请探究:若an=bn+c2(其中n>2),则△ABC可能的形状有哪些?请说明理由. 尝试证明因为an=bn+cn(其中n>2),所以a>b,a>c,即a为△ABC最大边.要证△ABC是锐角三角形,只需证cosA>0,即证a2 a2(bn+cn) 即证 bn+cn 亦即证 0 由上述可知,不等式成立.若an=bn+cn(其中n>2),则△ABC为锐角三角形. 评注解答这类数学开放题的策略是大胆猜测,小心求证.应抓住问题中那些影响结论的动态因素,通过取特例、分类讨论、构造图像,灵活运用数学知识,回顾相近或相似的题型、结论和方法等,大胆猜想,然后通过数学运算、合情推理、逻辑推理等手段,借助等价转化、数形结合等数学思维方法,小心求证猜想的结论.类似的高考题,如2018年江苏省数学高考试题第19题、2015年全国数学高考卷Ⅱ理科试题第20题等. 数学建模就是对实际问题进行数学抽象,用数学语言表达问题,用数学方法构建模型进行解题.一般考查如何把实际问题转化为数学问题的能力以及对不同模型的识别能力. 图1 例4如图1,在广场上,一盏路灯挂在一根4.5 m的电线杆顶上(电线杆的底部记为点A),假设把路灯看作是一个点光源S,身高1.5 m的女孩站在离点A处3 m的点B处,若女孩向点A前行2 m到达点D,然后从点D出发,绕着以BD为对角线的正方形走一圈,则女孩头顶的影子轨迹所围成的图形面积是______. 评注解决建模型应用题的策略是数学抽象,建立模型.建模解题的一般过程为:根据实际问题进行数学抽象,建立数学模型,运用数学知识与方法,求解模型、检验模型,最终获得实际问题的解.类似的高考题,如2018年全国数学高考卷Ⅱ理科试题第18题、2015年全国数学高考卷Ⅱ理科试题第12题等. 5.精题集萃 图2 1.如图2,已知三棱锥D-ABC,记二面角C-AB-D的平面角是θ,直线DA与平面ABC所成角是θ1,直线DA与BC所成角是θ2,则 ( ) A.θ≥θ1B.θ≤θ1C.θ≥θ2D.θ≤θ2 2.已知⊙C:(x-3)2+(y-4)2=1和点A(-m,0),B(m,0)(其中m>0),若⊙C上存在点P,使得∠APB=90°,则m的最大值是 ( ) A.7 B.6 C.5 D.4 图3 3.如图3,在正方体ABCD-A1B1C1D1中,点P是平面AA1D1D内的动点,且点P满足:直线PC1与平面AA1D1D所成角的大小等于平面PBC与平面AA1D1D所成角的锐二面角的大小,则点P的轨迹是 ( ) A.直线 B.圆 C.椭圆 D.抛物线 4.对于任意的实数x>0,不等式2ae2x-lnx+lna≥0恒成立,则实数a的最小值是 ( ) 7.定义在实数集R上的函数y=f(x)图像是连续不断的,若对于任意实数x,存在实常数h使得f(x+h)=-hf(x)恒成立,则称f(x)是一个“h”函数.下列关于“h”函数的结论: 1)f(x)=0是常数函数中唯一一个“h”函数; 3)f(x)=x2是一个“h”函数. 其中正确的个数是______. 图4 1)求椭圆C的方程. 2)设点P是椭圆上异于点A,B的任意一点,过点O作OM∥AP,ON∥PB,分别交椭圆于点M,N.问:△OMN的面积是否为定值?并证明你的结论. 参考答案 2)S△OMN为定值.设直线MN:y=kx+m,A(x1,y1),B(x2,y2),则 因为AP∥OM,BP∥ON,所以 即 x1x2+2y1y2=0. (1+2k2)x2+4kmx+2m2-4=0, 且 Δ=8(4k2+2-m2)>0. 由韦达定理可得 又x1x2+2y1y2=(1+2k2)x1x2+2km(x1+x2)+2m2=0,得1+2k2=m2.因为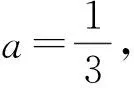
2 抓住关键“点”,选准“切入点”
3 抓住关键“点”,看准“着眼点”

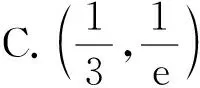
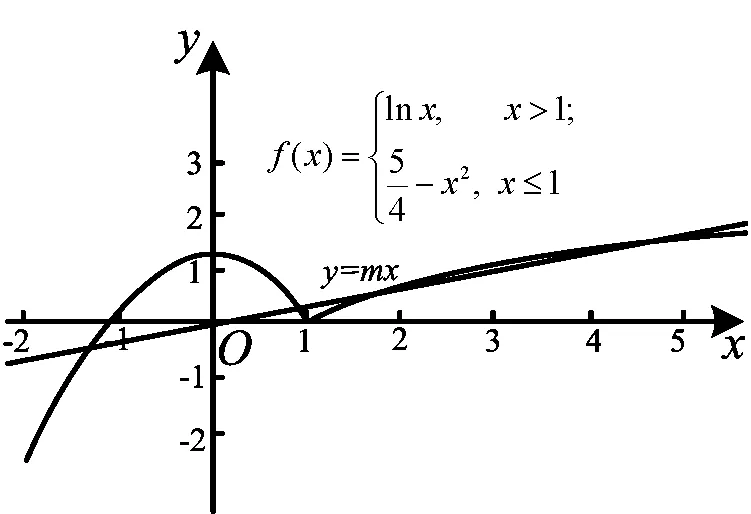

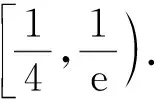
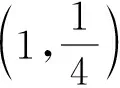
4 抓住关键“点”,把牢“着力点”
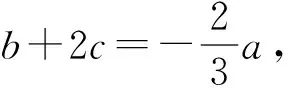
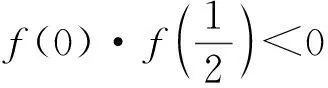
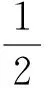
5 抓住关键“点”,立足“落脚点”

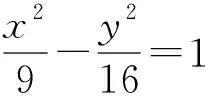

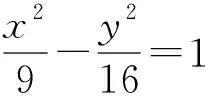
6 抓住关键“点”,巧用“平衡点”

7 抓住关键“点”,谨防“易错点”
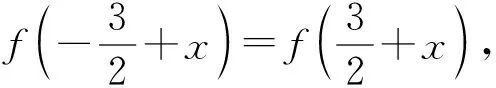
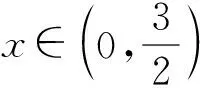
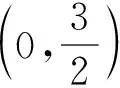
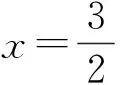
8 抓住关键“点”,把准“突破点”
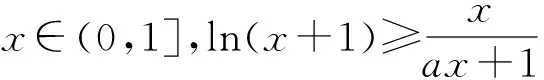






2 定义型
3 开放型
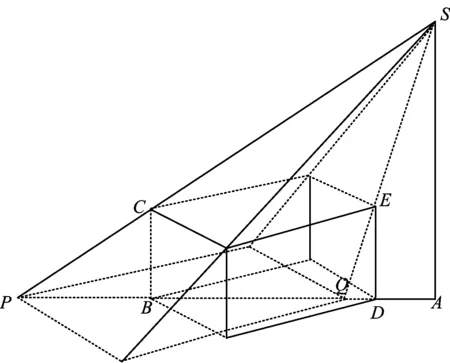
4 建模型应用题