一种基于双极性脉冲信号的沉底及掩埋小目标探测方法
岳雷
(昆明船舶设备研究试验中心,云南 昆明 650051)
0 引言
沉底及掩埋小目标的探测和识别一直是水声界的难题[1-2]。对于沉底小目标的探测,需要有足够高的空间分辨率,因此,探测信号需要有较高的距离分辨率和良好的混响抑制性能,检测波束需要有较高的空间角度分辨率;而对于掩埋目标,还需要考虑声波对海底有一定深度的穿透能力,探测信号的频率不能太高,通常在40 kHz以内[3]。
在混响严重的浅水环境下,回声定位海豚探测目标性能优于人工声纳[4]。文献[5-6]根据观测到的浅海海域海豚探测信号及其行为提出了仿生信号处理方法(双极性脉冲声纳处理方法),在海上完成了试验研究,结果表明气泡会非线性地散射等间距的等幅脉冲,而其他目标无此特性,这种非线性散射特性可用来辨识目标和气泡。文献[7]研究了双极性脉冲声纳处理方法在舰船尾流中探测目标的混响抑制性能,结果表明该方法要求硬件系统高保真,当目标回波信混比较高时,与常规声纳处理方法相比,该方法并未体现出优势。文献[8]采用双极性脉冲信号,分析了仿生信号处理机理,完成了试验验证等内容,提高了气泡环境下的目标探测性能。文献[9]采用双极性脉冲信号,借鉴双极性脉冲声纳处理方法,提高了杂波环境下的半导体、铁块等目标的分类识别能力。文献[10]认为混响是非线性散射体和部分线性散射体后向散射回波的叠加,采用双极性脉冲声纳处理方法完成了沉底小目标的探测,结果表明双极性脉冲信号及仿生信号处理方法可用于沉底目标的探测。然而,文献[8-10]所采用的双极性脉冲信号包络仅为高斯包络,且信号频段较高,而高频脉冲信号不能探测掩埋目标。文献[11]介绍了探测沉底及掩埋目标的算法处理流程,采用低频宽带(2~24 kHz)探测信号,通过研制的掩埋目标探测声纳,完成了探测掩埋金属板和混凝土块等目标的试验,表明低频宽带探测信号及其处理算法可区分海底沉积层和目标,但仅得到目标的距离信息,未获取目标的方位信息。
对于探测沉底或掩埋目标,文献[12]采用宽带预导向宽容Capon波束形成(SCRB)算法实现多波束探测。该算法将宽带信号划分为多个窄带信号,然后采用窄带宽容自适应波束形成在频域实现多波束输出,最后将多个频域进行反傅里叶变换再合成,从而得到宽带时域波束形成后的数据。然而该方法计算量较大,工程上实现较难,并未提高空间角度分辨率。
针对沉底及掩埋小目标的探测需求,本文首先提出采用低频宽带双极性脉冲信号作为探测信号,设计了信号参数,分析了信号的频谱、距离- 速度分辨及混响抑制能力;然后提出了无畸变高分辨多波束形成方法,结合仿生信号处理方法,提高了目标的空间分辨及混响抑制能力;最后在湖上搭建试验平台,根据主动声纳方程分析了试验系统探测沉底及掩埋钢管的目标回波信混比,处理并分析回波数据,完成了沉底钢管的试验验证。
1 探测信号设计及分析
1.1 低频双极性脉冲信号参数设计
双极性脉冲信号可表达为
s(t)=E(t)p(t)-E(t-τ0)p(t-τ0),
(1)
式中:t为时间;E(t)为包络;p(t)为填充的脉冲,通常为线性调频信号,即p(t)=exp[2πi(f0t+0.5ξt2)],f0为中心频率,ξ为调频率;τ0为脉冲间隔。
采用低频双极性脉冲作为探测信号,通过设计包络类型、中心频率、带宽、脉宽及脉冲间隔参数,获得优良的混响抑制及分辨能力。
针对沉底及掩埋小目标探测需求,包络的选取应主要考虑提高混响抑制能力;为保证探测信号对海底有一定穿透能力,设计信号最高频率不大于20 kHz;为保证探测信号有较强的混响抑制能力和较高的距离分辨率,在探测系统可实现的前提下,应尽可能采用大带宽探测信号;为提高信混比,在保证探测信号可累积足够周期(通常探测信号应不小于30个周期)回波的条件下,脉宽尽可能小;脉冲间隔根据探测系统和目标的距离来设计。本文设计的信号参数如表1所示。
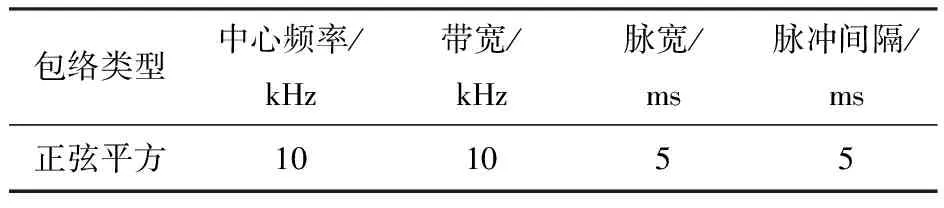
表1 信号参数
根据表1中的信号参数,仿真其时域、频谱及时频分布,如图1所示。
1.2 探测信号分析
1.2.1 宽带模糊度函数定义
探测信号的模糊度函数描述了信号在距离(时延)和速度(尺度)方面对目标的匹配滤波处理效果,对于宽带信号,其模糊度函数[10]定义为
(2)
式中:η为尺度,η=(c-v)/(c+v),c为声速,v为探测系统与目标相对运动速度;τ为时延;s(t)为探测信号;s*为探测信号取共轭。
可通过模糊度函数分析探测信号的分辨和混响抑制能力,其分辨能力可通过计算模糊度函数的主瓣宽度得到,其混响抑制能力可通过Q函数来分析,将模糊度函数在时延方向积分得到Q函数,其表达式为

(3)
信号Q函数值越小,表明其混响抑制能力越好,越有利于混响背景下的目标探测。
1.2.2 频谱分析
文献[8-10]中探测信号包络为高斯包络,即Eg(t)=exp[-(t-3σ)2/2σ2],σ=T/6,其傅里叶变换仍为高斯函数,T为信号脉宽。本文选取正弦平方包络,即Es(t)=sin2(πt/T),其傅里叶变换为

(4)
式中:f为频率。
由(4)式可知,Es(f)是主瓣宽度为4/T、旁瓣宽度为1/T的类正弦波动函数。
1.2.3 仿真分析
本文通过仿真方式进一步分析高斯包络和正弦平方包络线性调频信号频谱、分辨及混响抑制性能。
如图2所示为高斯包络和正弦平方包络线性调频(LFM)信号频谱、时延模糊度函数、尺度模糊度函数及Q函数图。仿真信号的Q函数时,以单频(CW)信号为参考,中心频率取10 kHz,脉宽取5 ms. 从图2可以看出:
1)正弦平方包络LFM信号频谱能量聚焦性优于高斯包络LFM信号;
2)正弦平方包络LFM信号的距离(时延)分辨能力优于高斯包络LFM信号;
3)正弦平方包络LFM信号的速度(尺度)分辨能力优于高斯包络LFM信号;
4)正弦平方包络LFM信号的混响抑制能力优于高斯包络LFM信号。
2 空间与时间联合探测方法
2.1 探测处理方法流程
本文提出的空间与时间(简称空时)联合探测方法,其处理流程如图3所示,包括信号调理、无畸变高分辨多波束形成、双极性脉冲声纳处理、希尔伯特变换4个步骤,其中,无畸变高分辨多波束形成和双极性脉冲声纳处理分别实现对目标的空域检测和时域检测,各步骤具体如下:
1)信号调理。将多通道检测基阵获取的原始回波经模拟滤波、放大处理。
2)无畸变高分辨多波束形成。将经过信号调理后的回波经模/数(A/D)转换采样后,进行混频处理、带通滤波、恒定束宽多波束形成后输出多个波束域时域信号。
3)双极性脉冲声纳处理。将多个波束域时域信号进行匹配滤波、分段后作减法、平滑滤波处理,获得不同波束域的距离估计信息。
4)希尔伯特变换。将不同波束域的距离估计信息进行希尔伯特变换,得到声成像图。
2.2 无畸变高分辨多波束形成
常规波束形成方法具有稳健性好、运算量小的优点,在实际工程中得到了广泛应用,但直接处理宽带信号会导致信号畸变;恒定束宽波束设计思想的实质就是采用某种方法使不同频率成分所形成的波束形状与频率分量无关[13],从而获取高保真回波,有利于后续的处理。本文在恒定束宽波束形成方法的基础上,提出了无畸变高分辨多波束形成方法,可进一步提高目标的空间角度分辨能力。
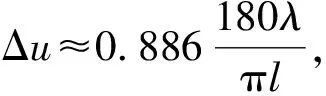
无畸变高分辨多波束形成方法具体步骤为:
1)混频处理。设阵元个数为M,则M阵元检测阵的接收信号为x(t)=[x1(t)x2(t) …xm(t) …xM(t)]T,m=1,2,…,M,将每一通道的接收信号经希尔伯特变换得到其解析信号形式,即

(5)
(6)

2)带通滤波。为便于后续波束形成处理,采用具有线性相位特性的有限冲击响应(FIR)带通滤波器组,将宽带信号划分为多个子带信号,每一个子带信号满足窄带条件。
3)恒定束宽多波束形成。所谓“恒定束宽”就是当接收宽带信号时,它能在给定频带宽度内的各个频率分量上,都保持具有近似相等的主瓣宽度[13]。针对不同频带,采用空间重采样法、最小二乘法等,设计不同的阵元权系数,即可实现线列阵的恒定束宽。本文采用空间重采样法设计不同阵元的权系数,通过调整空间导向矢量矩阵中的方位角θ实现多波束形成。
M阵元接收阵的空间导向矢量[8]为
(7)
式中:下标j表示不同频率的索引值;下标k表示不同检测角度的索引值。
方向矩阵为
A=[a(θ1,fj),a(θ2,fj),…,a(θk,fj),…,a(θK,fj)].
(8)
幅度束控窗函数矢量为wM×1,可为矩形窗、切比雪夫窗、自适应窗等窗函数系数。
阵列在K个方向上经波束形成后的输出信号为
y(θk,t)=[(w×1)⊕A]Txn(t),
(9)
式中:1为1×K维的全1矢量;⊕表示Hadamard积;xn(t)为对x(t)经过混频处理后的时域信号。
2.3 双极性脉冲声纳处理
双极性脉冲声纳处理方法由Leighton提出[5-7],可增强回波的线性散射,同时抑制回波的非线性散射。
探测信号为双极性脉冲信号,其表达式为
(10)
式中:Γ1(t)和Γ2(t)表示2个极性相反、有时延间隔的包络调制脉冲,即Γ1(t)=Γ(t),Γ2(t)=-Γ(t-τ).
在双极性脉冲信号激励下, 目标散射为线性,Γ1(t)的响应为
(11)
式中:h(t)为系统冲击函数。Γ2(t)和Γ1(t)相位相反,其响应为
(12)
将z1(t)和z2(t)的匹配滤波输出分别表示为Z1(t)和Z2(t),将Z1(t)和Z2(t)峰值对准作减法后记为Z-,Z1(t)和Z2(t)峰值对准作加法后记为Z+. 由于相位相反的2个脉冲通过非线性系统时,其散射不是按线性关系变化的,此时Z+≠0,Z-<2Z1(t);当其通过线性系统时,Z+=0,Z-=2Z1(t)。对于目标回波,Z-=2Z1(t),对于混响,由于混响是非线性散射体和部分线性散射体后向散射回波的叠加[10],Z-<2Z1(t),即采用双极性脉冲声纳处理方法可提高混响抑制性能。
采用双极性脉冲声纳处理方法,完成对波束形成后的时域信号处理,具体步骤如下:
1)将波束形成后的信号进行匹配滤波处理,匹配滤波的冲击响应函数选取为Γ(t);
2)将匹配滤波输出结果分成两段(可相干累加)作减法;
3)用短时窗对作减法后的信号平滑滤波。
3 试验验证
3.1 试验方案
为验证理论分析及仿真计算,在某湖搭建试验平台,试验水域水深超过20 m,湖底为泥沙质沉积层,沉积层以下2 m范围内有小石块。设计的探测沉底钢管试验方案如图4所示。基阵支架固定在试验船行车架上,声探测基阵(包括声发射基阵和声检测基阵)固定在基阵支架上,声探测基阵的安装倾角α可调,其背面安装凹槽状吸声橡胶,抑制湖面反射回波;钢管位于湖底,声探测基阵距湖底高度H,与钢管水平距离L,与钢管直线距离D. 试验参数设计如表2所示,采用的试验设备实物如图5所示。

表2 试验参数
试验中,发射基阵为2×2面阵形式,阵元间距0.14 m,声源级194 dB;检测基阵为2×24面阵形式,阵元间距0.07 m,水听器灵敏度-202 dB;目标为长度2 m、外径0.22 m、壁厚0.01 m的空心圆柱体钢管。
3.2 探测沉底目标回波信混比分析
由主动声纳方程可知,目标回声级[14-15]为
EL=SL-2TL+TS,
(13)
海底混响级为
(14)
则目标回波信混比为
(15)
(16)
式中:SL为声源级;TL为传播损失;TS为有限长圆柱体的目标强度;Sb=-27+10lg (sin2φ)为海底散射强度,φ为掠射角,φ=90°-α;r为探测基阵到海底探测区域的距离;φ为基阵的等效合成束宽;rt为有限长圆柱体的半径;κ为波数;β为声波与目标法线方向的夹角(声波入射角)。
目标回波信混比srr与目标强度TS、海底散射强度Sb、信号脉宽T、探测距离r、基阵等效合成束宽φ有关,通过增大钢管的长度和半径、声探测基阵的孔径,减小探测距离、探测信号脉宽的方式均可提高目标回波信混比。当探测信号脉宽、声探测基阵参数、探测距离、目标参数等确定后,影响srr的参数只有β.
将有关参数代入(15)式,使β在-10°~10°范围变化,得到目标回波信混比随声波入射角变化曲线,如图6所示。从图6中可以看出,srr随着β变化呈周期性变化,在较多角度出现srr<0的情况下,在-2°~2°角度范围无周期变化,该角度范围内目标回波信混比随声波入射角变化情况如表3所示。当入射角为2°时,目标回波信混比为-2.9 dB,此时很难检测到目标,这种周期性变化会降低检测概率。通过提高目标回波信混比、信混比随入射角变化的周期的方式,可提高检测概率。

表3 目标回波信混比随声波入射角变化情况
由(15)式可知,通过减小海底散射强度Sb(即减小掠射角φ)、基阵的等效合成束宽φ(采用窄波束方式),可提高目标回波信混比。
由(16)式可知,影响信混比随入射角变化周期的因素是波数κ(即频率f),通过仿真方式计算不同频率下-3 dB回波信混比对应的最大信号入射角,结果如图7所示。从图7中可以看出,当频率升高后,入射角明显下降,即低频有利于提高探测入射角。
因此,在探测有限长沉底圆柱体目标时,宜采用低频、窄波束、小掠射角方式。
3.3 探测掩埋目标回波信混比分析
对海底作出一些假定后,可以将自由空间中的物理声学方法——Kirchhoff近似法推广到掩埋情况,用来计算海底掩埋目标的回波信混比[16]。
图8为掩埋钢管探测示意图,信号以入射角γi从水介质中发射,以透射角γt穿透沉积层探测到管道,最后回波原路返回,信号在沉积层中传播到钢管的直线距离为rc.
掩埋目标的目标强度重新定义[16]为
TS=TS0+Δt+Δa,
(17)
式中:TS0表示沉积层中目标强度;Δt表示声波经过两次透射引起的目标强度变化量;Δa表示声波在沉积层中双程传播衰减导致的目标强度变化量,
(18)
Δa≈-2μfrc,
(19)
(20)
(21)

(22)
μ为吸收系数,cw为声波在水中传播速度,cs为声波在沉积层中传播速度,ρw为水密度,ρs为沉积层密度。
重新定义的目标强度和沉积层特性有关,沉积层类型及参数如表4所示。
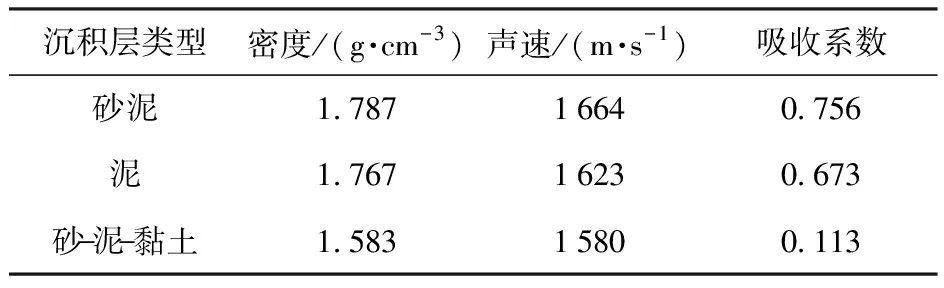
表4 沉积层类型及参数[15]
将(17)式~(22)式代入(15)式,仅考虑声波入射角β=0°的情况,掠射角φ=45°,沉积层参数如表4所示,绘制出目标回波信混比随掩埋深度变化曲线如图9所示。以3 dB为检测门限,由图9可以看出:当沉积层分别为砂泥、泥、砂泥- 泥- 黏土时,钢管掩埋深度分别小于1.22 m、1.29 m、7.02 m即可检测到目标。
由(15)式~(22)式可以看出,当沉积层和目标确定后,除采用窄波束方式提高目标回波信混比外,还可通过改变信号频率和掠射角方式提高目标回波信混比。
当频率减小时,TS0虽然也在减小,但其按对数方式减小,而声波在沉积层中双程传播衰减导致的目标强度变化量Δa≈-2μfrc按线性方式增大,即当频率减小时,目标回波信混比增大。
为考察掠射角对目标回波信混比的影响,根据(15)式~(22)式,计算不同掠射角(30°~60°)下检测门限为6 dB时可探测到目标的最大掩埋深度,结果如图10所示。从图10中可以看出,在30°~60°范围内,随掠射角增大,可探测到目标的最大掩埋深度减小,即掩埋目标回波信混比随掠射角增大而减小。
因此,在探测掩埋有限长圆柱体目标时,应采用低频、窄波束、小掠射角方式。
3.4 试验数据处理及分析
将采集的24通道信号取前100 ms处理,由于发射基阵和检测基阵距离较近,发射基阵刚发射信号时,检测基阵就接收到发射信号,实际处理时直接去掉前15 ms数据,其频谱能量集中在5~15 kHz之间。
将24通道回波数据进行混频处理,混频的倍数n取10,经混频处理后的时域波形变得更加密集,其频谱展宽,从之前的5~15 kHz变到50~150 kHz. 经混频处理后的24通道回波时域波形如图11所示。
将50~150 kHz频带均匀地划分成10个子带,选取切比雪夫窗,阵元个数24、旁瓣级-30 dB,设计的恒定束宽波束主瓣基本上保持恒定,其波束如图12所示。
经恒定束宽多波束形成后得到的不同角度波束目标回波时域如图13所示。由图13可以看出,0°波束目标回波能量最强, 1°波束目标回波能量大于-1°波束目标回波能量,可初步判断目标方位在0°~1°之间。
采用本文提出的空时联合探测方法,对24通道回波进行处理,结果如图14所示。图14中,Gau和Sin分别表示高斯包络和正弦平方包络双极性脉冲信号,Mf和Twips分别表示匹配滤波处理和双极性脉冲声纳处理。
由图14(a)可以看出:估计的目标方位角为0.4°,其空间角分辨能力可达0.5°. 从图14(b)中可以看出:正弦平方包络双极性脉冲信号的混响抑制性能略优于高斯包络双极性脉冲信号;采用匹配滤波处理方法时混响较强,采用双极性脉冲声纳处理方法时混响得到了有效抑制,同时表明双极性脉冲信号混响抑制性能优于单个线性调频信号;估计的目标距离为31.8 m,实际目标距离为(23.42+21.02)1/2=31.4 m.
将不同波束域的目标回波进行双极性脉冲声纳处理,并进行希尔伯特变换,得到目标声成像如图15所示。
4 结论
本文根据沉底及掩埋小目标探测需求,设计并分析了低频双极性脉冲信号,提出了基于双极性脉冲信号的空时联合探测方法,设计了探测沉底钢管的试验方案,完成了回波获取试验,分析了声探测沉底和掩埋有限长圆柱体目标回波信混比情况、试验数据处理结果。目标回波信混比分析情况及试验数据处理结果表明:
1)低频、窄波束、小掠射角方式有利于探测沉底和掩埋有限长圆柱体目标。
2)设计的低频双极性脉冲信号及提出的空时联合探测方法可明显提高目标的空间角度分辨能力和混响抑制性能。

