筒射串翼无人机展开动力学分析

陈方正， 于剑桥, 沈元川， 马安鹏

(1.北京理工大学 宇航学院, 北京 100081; 2.淮海工业集团有限公司, 山西 长治 046012)

0 引言

采用发射筒发射的方式往往对飞行器的气动面面积具有很大限制，可折叠串列翼布局能够大大增加筒射无人机的翼面积，从而提高无人机的低速性能和滞空时间。因此串翼布局广泛应用于各种筒式发射巡飞器[1]，如美国的“弹簧刀”巡飞器、“郊狼”无人机以及俄罗斯“R-90”侦查巡飞器均采用可折叠串翼式布局。

对于串翼布局及相应飞行器的研究主要集中在气动特性领域。Rhodes等[2]、Rokhsaz等[3]和Chen等[4]分别通过理论计算和数值模拟方法研究了串翼布局的气动特性，并指出在某些情况下串翼布局的气动性能优于单翼布局。Khan等[5]、Scharpf等[6]和Jones等[7]通过风洞实验方法证实了上述结论，并对串翼布局在低雷诺数下的流动机理进行了研究。在串翼飞行器研究方面，陶福兴等[8]设计了串翼布局巡飞器的气动外形，并对其性能进行了分析。李永泽等[9]比较了展开状态下不同布局串翼飞行器的气动特性。Zhang等[10]和Gao等[11]分别研究了采用不同机翼展开方式的串翼无人机在展开过程中的动态气动特性和铰链力矩变化。然而对包含动力学响应的折叠串翼无人机发射展开过程尚缺乏必要的研究。

可折叠串翼无人机在发射筒内机翼折叠，发射离筒后4片大展弦比机翼迅速展开到位，之后动力及控制系统开始工作。串翼无人机离筒展开过程类似于飞行器变体过程[12]，其气动外形和质量特性均发生剧烈变化，并且此时飞行器处于无控状态，其展开过程产生的扰动对于无人机的正常发射有较大影响。已有研究[13-18]对飞行器变体过程的气动特性变化、动力学问题以及控制问题进行了分析。但是其通常假设的变化速度较慢，不能很好地体现由于多刚体快速运动引起的惯性力和惯性力矩的作用。

本文以折叠串翼无人机为研究对象，基于串翼无人机展开过程气动准静态假设，结合多体动力学模型，通过仿真手段确定串翼无人机机翼快速展开过程中的动力学响应、分析机翼展开时间和展开顺序对弹道扰动大小的影响，以期为展开机构的设计提供参考。

1 筒射串翼无人机方案

某串翼无人机模型如图1所示，前、后机翼交叠布置，前翼位于机体上方，后翼位于机体下方。处于折叠状态时，前、后机翼分别绕各自转轴向后方或者前方折叠，折叠后的无人机截面为正方形，可以放入发射筒中，折叠状态串翼无人机如图1(a)所示。当无人机发射离筒后，各机翼在弹簧扭力的驱动下绕各自转轴旋转展开，展开方式如图1(b)所示。所有机翼展开到位后，控制系统启控，发动机开始工作。由于机翼近似对称展开，可以只研究展开过程的纵向动力学特性。垂直尾翼对本文研究内容影响不大，不予考虑。

2 多体动力学建模

无人机展开的过程中，其质量特性因为外形的迅速改变而变化，传统的单刚体动力学模型不能反映其展开过程中的动力学特性。因此，本文基于Newton-Euler方法[15]，将机体和各个机翼分别看作不同的刚体，建立描述串翼无人机展开过程的多刚体模型。

2.1 坐标系及变量定义

如图2所示，以机体质心OB作为机体坐标系原点，OBxByBzB作为机体坐标系，Axyz作为地面坐标系。图2中：下标B表示机体，下标i=1,2,3,4分别表示图2中的各个机翼；地面坐标系原点到机体坐标系原点的矢径为rAOB；Ci点为机翼i的质心；机体坐标系原点OB到Ci点的矢径为rOBCi；地面坐标系原点A到Ci点的矢径为rACi；机翼i上任意一点表示为Si；机体坐标系原点OB到Si的矢径为rOBSi；Ci到Si的矢量为rCiSi；地面坐标系原点A到Si的矢量为rASi.

机翼坐标系Cixiyizi如图3所示：坐标系原点为机翼质心Ci，xi与机翼展长平行，zi位于机翼旋转平面内，与机翼弦长平行，yi根据右手定则确定；Li为机翼转轴到第i个机翼质心的距离；χi为机翼旋转展开的角度，χ1和χ4为正，χ2和χ3为负。

2.2 动力学模型建立

基于Newton-Euler法建立折叠串翼无人机多体动力学模型[15]。

2.2.1 平动动力学模型

分别对机体和4片机翼分别列写动量定理如下：

(1)

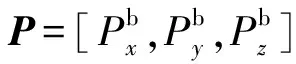
(2)

(3)

该项表征了由于机翼质心相对机体的运动产生的动态附加项。

2.2.2 转动动力学模型

为使机翼与机体之间的相互作用力矩抵消，需使各个刚体所受外力矩作用点统一。将机翼与机体所受外力矩作用点选在机体坐标系原点。对于第i个机翼，应用质点系对动点的动量矩定理[19]：

(4)

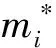
(5)

根据图2可知有如下几何关系：

(6)

代入(5)式，最终化简得

(7)

对机体和各个机翼分别列写动量矩定理：

(8)

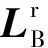
(9)

由(9)式可知，串翼无人机展开过程中其转动动力学方程与外形变化引起的气动力变化、质心位置变化以及机翼转动引起的附加力矩有关。

2.3 纵向动力学方程

基于图3，机体质心OB到机翼i质心Ci的矢径rOBCi在机体坐标系中可以表示为

(10)

(11)

在机翼坐标系下机翼i转动惯量可近似为

(12)

将其转换到机体坐标系下，得

(13)

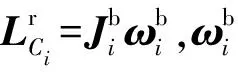
(14)

(15)

将(11)式和(15)式代入(2)式和(9)式，投影到机体坐标系，并补充运动学方程，最终得到的串翼无人机展开纵向动力学方程为

式中：vbOBx、vbOBy分别为机体速度在机体系OBxB和OByB轴上的分量；ϑ为俯仰角；x和y为飞行器机体质心位置在地面系的坐标。由(16)式和(17)式可知，纵向动力学方程和绕机体质心转动动力学模型存在耦合及附加项，远比飞行器单刚体纵向动力学模型复杂。其中含有机翼旋转角度和角加速度关联的项表征了飞行器外形变化率引起的附加惯性力和力矩，体现了机翼旋转的动态过程对动力学模型的影响。

3 展开过程非定常气动力的计算

为了研究机翼展开过程中的非定常气动效应，对攻角α=0°、展开时间不同时折叠串翼无人机展开过程进行数值模拟。使用计算流体力学分析软件ANSYS Fluent进行计算，控制方程为Navier-Stokes方程。由于流速低，认为气体不可压缩，且不考虑能量方程。使用速度入口和压力出口作为边界条件，来流速度为v=30 m/s，湍流模型为标准k-ω湍流模型。对流项采用2阶迎风格式，计算方法为Coupled算法，时间步长为T/200，其中T为整个机翼展开过程时间。

使用计算流体力学(CFD)方法对可动区域进行计算通常可以采用动网格方法或者嵌套动网格方法[10,20-21]。嵌套网格将计算域分割成多块具有重叠或者嵌套的子网格。当物体运动时，贴体部件网格随之运动，数值计算在各个子网格上分别进行，并在重叠或者嵌套的区域通过插值的方法来传递流场信息[22]。使用嵌套动网格降低了网格生成的难度，一方面可以保证机翼附近边界层网格不发生改变，保证边界层网格的质量，避免了动网格设置不当产生的网格畸变；另一方面嵌套网格更新时仅需要重新选择插值供体单元，不用重新计算网格生成，计算量小于动网格。

对于本文研究的对象，将包含机体的整个计算域作为背景，生成非结构背景网格，使用结构网格生成各个机翼的部件网格(见图4)。将部件网格与背景网格进行组装，通过Fluent软件中的UDF命令控制机翼展开角速度。背景网格和部件网格组成了计算域中的混合网格系统，如图5所示。

折叠串翼无人机在离筒后，各个机翼在扭簧力矩的作用下迅速展开。根据扭簧的力学特点和动量矩定理，容易推导得到机翼展开的运动规律为

χi(t)=π2[1-cos (π2Tt)]，0≤t≤T.

(18)

T决定了机翼完全展开的时间，与扭簧性能和机翼质量特性密切相关，机翼开始展开的时间可由专门设计的机构控制。

图6为将展开时间进行归一化处理后，展开时间T分别为0.20 s、0.50 s、1.00 s、5.00 s时串翼无人机机翼同时展开过程的升力系数CL、阻力系数CD和俯仰力矩系数CMz变化曲线(v=30 m/s，α=0°)以及相应展开角度下定常状态气动特性。

由图6可知，展开过程中前翼(后翼)的后掠角(前掠角)逐渐减小，迎风面积增大，从而导致整体升力系数和阻力系数逐渐增大。当归一化时间参数t/T<0.4时，由于展开角度很小，前(后)机翼后(前)掠角很大，机翼产生升力很小，因此升力系数变化不大；当t/T>0.4以后，前(后)机翼的后(前)掠角减小引起的升力增加开始变得明显，从而导致整体升力系数迅速增大，机翼展开过程中，由于升力的大小和压心位置均不断变化，对俯仰力矩也产生了影响；当t/T=0.7时，前后机翼已经产生了可观的升力，但是由于机翼展开角度的原因使得其压心位于机体坐标系原点之后，产生低头力矩。随着展开角度的增大，升力和压心位置进一步变化，产生了抬头力矩。

尽管展开时间不同，计算得到的非定常阻力和俯仰力矩系数与定常状态相比差别很小，而升力系数变化趋势相同。但是当t/T>0.6时，随着展开时间的缩短，非定常升力系数与定常升力系数差别逐渐增大。当T=0.20 s时差异较为明显，当t/T=1.0时，相差约12%. 这主要是因为机翼旋转引起的附加速度增加了机翼的升力。但是由于机翼长度较短，在很大展开时间范围内(如T>0.20 s)，这种由于机翼旋转展开引起的附加速度与来流速度相比仍然较小，使用定常气动数据计算不会带来很大误差。然而当展开时间很短时，非定常展开过程中气动特性变化更为剧烈，会对计算带来一定误差。但是其基本变化趋势与定常状态一致。因此在分析展开过程动态响应时，仍然可以使用气动准定常假设。

4 离筒展开过程动态响应与分析

结合建立的多体动力学模型和展开过程气动参数变化，对折叠串翼无人机发射离筒后的无控展开过程进行动力学仿真。气动特性变化是影响串翼无人机展开动态响应的重要因素之一。根据准定常假设，串翼折叠无人机展开过程的气动参数可以根据不同时刻机翼展开角度插值稳态气动数据得到。动导数部分使用DATCOM软件计算得到。以折叠串翼无人机离筒瞬间作为仿真起始点。此时α=0°，发射速度为30 m/s，发射角度为45°. 单片机翼质量mi=0.1 kg，机体质量mB=1.6 kg.

4.1 展开速度对动态响应的影响

假设折叠串翼无人机发射离筒后，前后机翼展开角度变化相同，使用稳态气动数据，分别设定展开时间T分别为0.02 s、0.05 s、0.20 s、0.50 s、1.00 s，将相应的χi、χ·i和χ··i变化规律代入(16)式和(17)式，进行纵向动力学仿真，展开角度χ、攻角α、俯仰角速度ωbz、速度v以及纵向弹道(高度为y，水平距离为x)变化如图7所示。

由图7可知，当展开时间极短时(T=0.02 s)，无人机刚刚离开发射筒便产生了极大的俯仰角速度和较大的攻角。考虑到此种状态下，非定常气动特性相比于定常气动特性变化更为剧烈，因此实际无人机姿态扰动可能更加剧烈。虽然无人机迅速完成了展开过程，进入静稳定状态，但是由于初始产生的扰动较大，在无控状态下，无人机攻角和俯仰角速度在收敛的过程中波动仍然较大，正是这种波动导致了无人机速度和射程的迅速降低。随着展开时间变长，无人机发射过程产生的攻角和俯仰角速度波动逐渐减小，速度降低变得缓慢，射程有一定的提高。然而当时间较长时(T=1.00 s)，虽然没有在一开始离筒时便产生较大的攻角波动，但是在展开过程中也出现了较大的攻角和俯仰角速度波动。由于无人机展开时间变长，其在离筒后较长时间处于机翼未完全展开状态，阻力较低，导致其速度降低反而低于T=0.20 s的状态，并且射程有进一步提高。

对于采用筒式发射的无人机而言，总是希望其在离筒后姿态波动尽量小，同时在展开完成时具有一定的高度和相当的速度存量。对于图7中所示各种展开状态，显然T=0.20 s时，展开扰动最小。

4.2 展开过程中气动特性变化和变形速率的影响

由(16)式可知，折叠串翼无人机在展开过程中产生扰动的主要原因有：1)由于外形变化引起的气动力和气动力矩变化； 2)外形变形速率引起的附加惯性力和力矩作用。为了明确展开过程中气动特性和惯性作用对纵向动态响应的影响，在4.1节基础上进一步进行仿真验证，结果如图8所示。

为了研究气动参数变化对动态响应的影响，在整个展开过程中均使用展开构型的气动参数，其他仿真参数与4.1节相同，分别对不同展开时间进行仿真。T=1.00 s时，纵向动态响应如图8所示。 由图8可见：当展开速度较快时，气动力变化也较快，对动态响应产生的累积效应有限；当展开时间较长时，气动参数的变化影响明显。由于无人机由折叠到展开过程中气动特性由静不稳定变为静稳定，在展开时间较长时，初始的静不稳定状态引起了姿态的较大扰动。

为了研究展开过程中外形变化速率引起的附加惯性力和力矩的影响，令机翼转动角速度和角加速度值均为0(χ·i=0°/s，χ··i=0°/s2，i=1，3)。其他仿真条件如4.1节所示。当T=0.02 s时，仿真结果如图8所示。由图8可见，当无人机外形变化很快时，气动力对纵向扰动的作用并不明显，而由于机翼转动动态过程产生的附加惯性力和力矩成为主要扰动因素。当不考虑机翼转动速度和转动加速度时，扰动大大减小。

因此可以确定，当展开速度较快时，外形变化速率引起的附加惯性力和力矩是扰动产生的主要原因；当变形速率较小时，惯性力和力矩减小，而此时由于外形变化引起的气动参数变化成为产生扰动的主要原因。

4.3 不同展开顺序对动态响应的影响

改变串翼无人机前后机翼的展开顺序，使其依次展开，研究机翼不同展开顺序对展开过程动态响应的影响。假设前后机翼展开时间相等，为0.714T，展开时间差为0.286T. 其他条件不变，分别对后翼先展开和前翼先展开两种状态，不同展开时间进行动力学仿真。

图9为后翼先展开时无人机纵向动力学响应。由图9可见，当展开时间很短时(T=0.02 s)，攻角和俯仰角速度的响应值要大于图7中的相应值。这是因为单个机翼展开时间实际仅为0.714T，机翼实际展开速度更快；同时由于两个机翼不是同时展开，机翼旋转产生的附加惯性力和力矩不能抵消，使得在展开时间很短的情况下，后机翼和前机翼依次展开的情形扰动更大。然而比较图9和图7中T=1.00 s时的曲线可以发现，后机翼先于前机翼展开的情形扰动较小。图9中T=2.50 s时攻角扰动仅略大于图7中T=1.00 s的攻角扰动。这主要是因为后机翼先于前机翼展开，t/T相同时具有更大的静稳定性，使得发射弹道在此种情况下更加稳定。

图10为前机翼先展开时，无人机纵向动力学响应。当展开时间很短时，与图9中T=0.02 s攻角变化类似，扰动大于相同展开时间时机翼同时展开的情况。但是当展开时间较长时由于前翼先于后翼展开，无人机更长时间处于气动静不稳定状态，因此在T=0.50 s，攻角扰动水平便达到了图7中T=1.00 s时攻角的扰动水平。进一步增加时间，弹道发散，因此采用前翼先于后翼展开的方法不利于发射段弹道的稳定。

总结以上分析可知，当展开时间较短时，无论何种展开方式均会对初始段弹道产生较大扰动；当展开时间较长时，无人机后翼先展开，有利于其发射展开过程的稳定，使得允许的展开时间更长一些，相反，前翼先展开，不利于无人机发射展开过程的稳定，使得展开时间较短时即产生了较大扰动。

5 结论

本文基于Newton-Euler法建立了描述筒射串翼无人机展开过程的多体动力学模型，通过嵌套动网格技术分析了串翼无人机展开过程中定攻角状态下的非定常气动特性变化。基于气动准静态假设和多体动力学模型，重点研究了串翼无人机发射展开过程中，机翼不同展开速度、展开顺序对发射无控展开段弹道的扰动特性。主要结论如下：

1)机翼展开时间对无人机发射展开段弹道的扰动有较大影响，展开时间过短或者过长都不利于发射段弹道的稳定。对于本文研究的筒射折叠串翼无人机，展开时间为0.20 s，前后机翼同时展开时对发射弹道扰动最小。

2)当机翼展开时间过短时，由于外形变化速率引起的附加惯性力和力矩对扰动起主要作用；当机翼展开时间较长时，气动力和力矩变化对扰动起主要作用。

3)考虑到前后机翼不同的展开顺序可知，前翼先展开不利于发射展开段弹道的稳定，允许最大展开时间较小。后翼先展开，有利于发射弹道的稳定，允许最大展开时间较大。

4)机翼展开时间越短，展开速度越快时，展开过程中非定常气动力效应越明显，与气动准静态假设的误差增大。这种情况下无人机展开过程动态响应将更加剧烈，但是对于展开时间与扰动的关系没有本质影响。本研究可以为展开机构的设计提供参考依据。