基于kd_tree算法和法向量估计的点云数据精简方法

王 丽

宿州学院环境与测绘工程学院，安徽宿州，234000

地面三维激光扫描技术是近年发展起来的一种新的获取空间三维信息的技术方法，其通过非接触式扫描快速获取物体表面信息，扫描的数据以离散点云形式存储。数据具有高精度的特点，但同时包含物体信息的海量点云数据为后续数据处理带来困难，几十万甚至上百万的点云数据不仅影响数据处理的进程，而且还影响结果的精度。为此，近几年国内外学者都在保证点云特征和精度的前提下，致力于研究点云数据精简的算法。如HAMANN等提出对于不同平面实体曲线重建点云简化方法[1]；WEIR等提出包围盒算法，实现点云简化[2]；邢正全等提出正方体栅格划分实现K近邻搜索，利用法向量特征实现点云简化[3]；马振国提出利用kd_tree索引实现点云数据结构划分，并且结合点云曲率特征实现点云简化[4]，该方法需手动介入，自动化程度不够。本文考虑三维数据结构特点，提出一种基于kd_tree索引算法的法向量估计点云数据精简方法。该方法利用kd_tree算法构建空间数据树结构，搜索每个点K邻域点，搜索速度快，可提高数据简化速度，结合最小二乘原理拟合每个邻域点构成的平面，估计每个点的法向量，并进行法向量方向调整，计算每个点及其邻域点法向量的夹角，设定夹角阈值，如果大于阈值，则删除，从而实现点云数据精简。

1 点云数据精简方法

1.1 kd_tree算法

kd_tree索引算法是Friedman等人于1977年提出的一种数据检索方法，kd_tree是k-dimension tree的缩写，在K维空间对数据结构进行划分，通过K近邻查找即KNN算法，实现每个点K邻域点的搜索。kd_tree利用最大方差划分分裂维数，根据分裂维数所在结点确定根结点，通过根结点将空间数据划分为左右两个子空间，利用递归方法将左右子空间继续划分，直到所有点划分完[5](表1)。

1.2 KNN算法

KNN算法，全称是K-Nearest Neighbor algorithm，即K邻域算法。本文选取K邻域是选取距离P点欧式距离最近的K个点所组成的点的集合。计算P点的K近邻点，需求出P点与其余n-1个点的欧式距离，然后将计算的欧式距离按值由小到大排序，选取排列在前面的K个点即为P点的K近邻点。这种方法简单方便，但是对于海量点云而言，计算效率非常低，处理速度非常慢。因此本文首先利用kd_tree算法构建空间点云数据拓扑结构，在kd_tree空间树状结构上实现K近邻搜索，搜索效率明显提高。

1.3 点云法向量估计

对于每个点的法向量估计，结合最小二乘原理，对每个点的K邻域点进行局部拟合。在点云数据密集处，并且搜索半径不大情况下，每个点的法向量可以用局部拟合平面的法向量表示[6]。因此，利用最小二乘原理对每个点K邻域点进行平面拟合，计算公式如下：

表1 kd_tree结构构建算法表

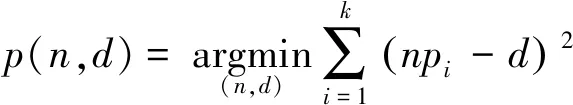
(1)

式中，n是局部拟合平面p的法向量，d表示拟合平面p到坐标原点的距离。

平面p的法向量通过主成分分析法，分析协方差矩阵A的最小特征值所对应的特征向量，此最小特征向量即为平面p的法向量。其中，协方差矩阵A公式如下：

(2)

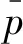
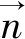
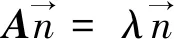
(3)

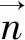
1.4 点云精简

点云数据记录每个点的三维坐标信息，属性信息可以反映出每个点所在位置、曲率等信息，曲率的大小反映局部曲面特征点信息的分布情况，曲率大则表明点云局部表面在该点变化剧烈，曲率小则表明点云局部表面在该点变化缓慢，特征不明显，因此，可以利用曲率大小剔除非特征点[7]。同时，曲率的大小可以通过邻域点法向量夹角的大小反映。邻域点法向量夹角越大，则曲率变化不明显；反之，如果邻域点法向量夹角越小，则曲率变化越明显[8]。因此，可以设置阈值τ，如果邻域点法向量夹角小于阈值，则作为特征点保留，将邻域点法向量夹角大于阈值的点作为非特征点删除。这样，实现利用邻域点法向量特征实现点云数据精简。

通过kd_tree算法实现点云数据空间结构树状划分，搜索每个点K邻域点(K一般最小取10，最大取20)，利用最小二乘原理拟合K邻域点最佳平面[9]，计算平面法向量即每个点的法向量，通过法向量夹角大小和阈值比较，实现点云数据精简。具体点云精简流程如图1。

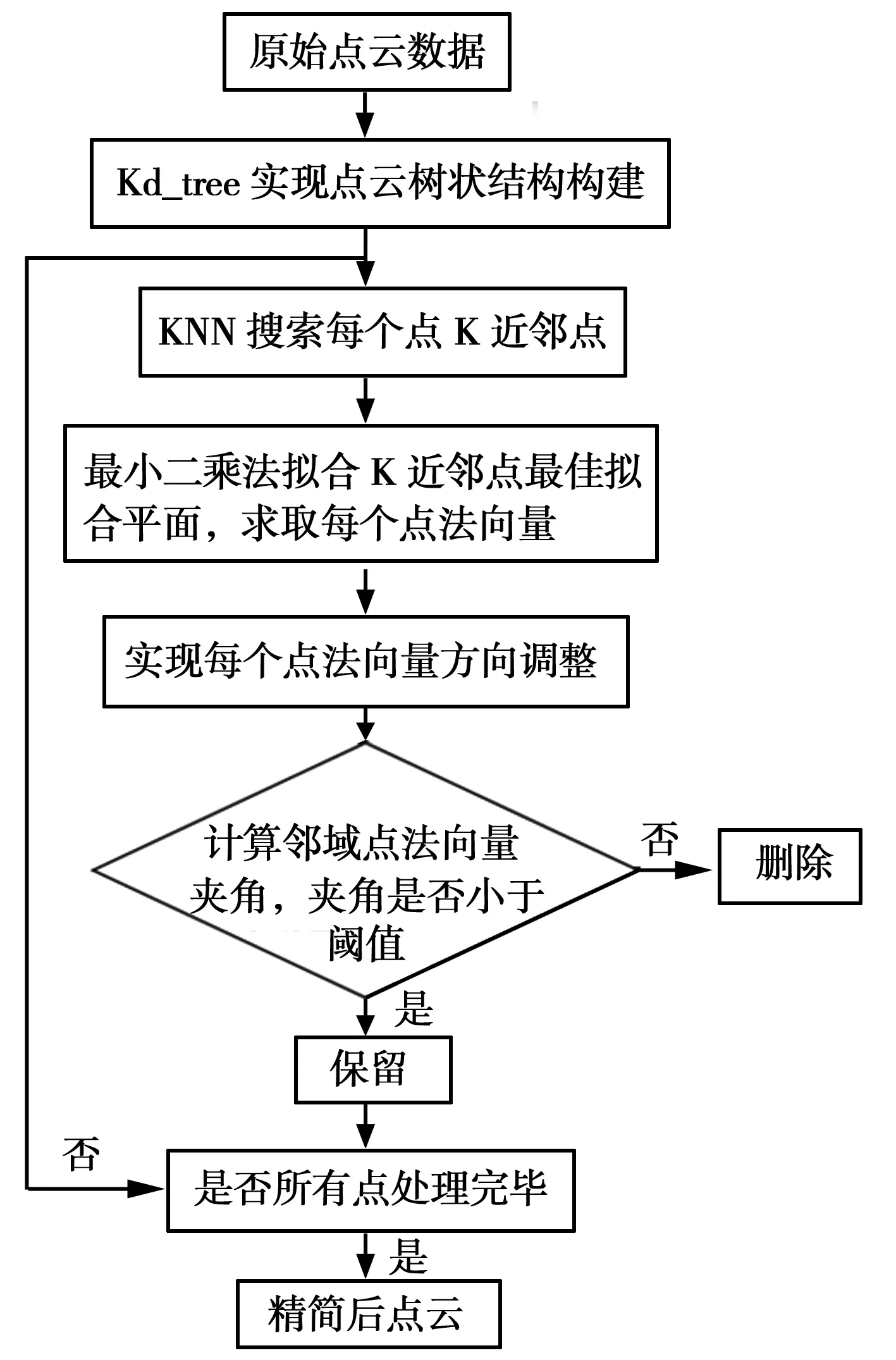
图1 点云精简流程图

2 实证分析

实验选取一把椅子点云数据，数据处理利用MATLAB2012b软件编程实现。实验对每个点选取K近邻点，通过最小二乘原理，拟合P点的平面方程，计算每个平面的法向量即为P点的法向量。

本实验通过对K值分别取10,15,20三个数值进行实验，对阈值τ选取5°，3°，2°进行实验，表2表示在阈值取5°时不同K值简化后的结果，表3表示阈值3°时不同K值简化后的结果。实验也对阈值取2°进行实验，但是点云简化结果并不理想。点云简化后显示模型如图2所示。

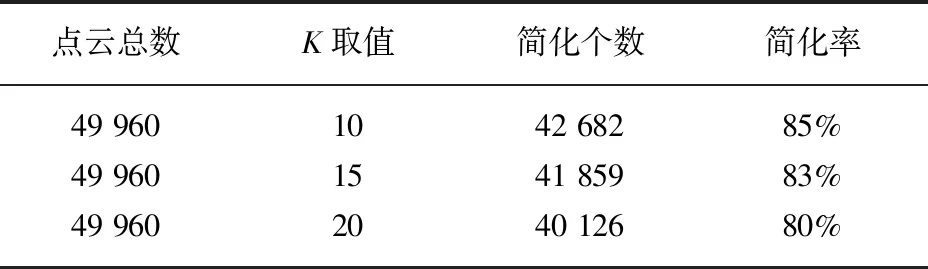
表2 阈值τ选取5°实验结果

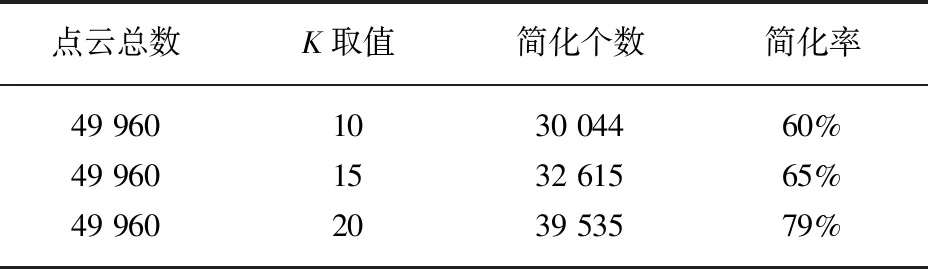
表3 阈值τ选取3°实验结果

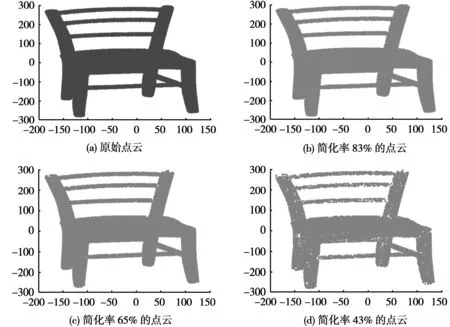
图2 点云模型图

本实验选取K=15。根据kd_tree搜索法，选取的每个点15个近邻点，前三个点近邻点如表4所示，前三个点法向量估计值如表5所示。

表4 前3个点15近邻

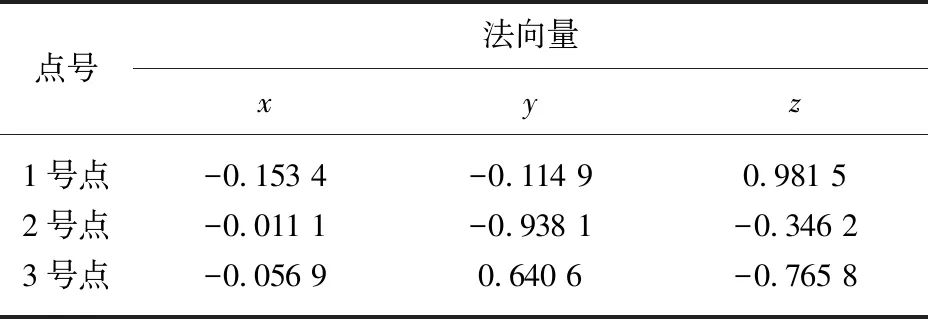
表5 前3个点法向量

表2表示夹角阈值取5°，K值取10,15,20时，点云简化率在80%左右。表3表示夹角阈值取3°，K值取10,15,20时，点云简化率在60%～70%左右。同时，图2的(b)(c)图反映点云在简化率83%和65%的椅子模型，和(a)图原始点云椅子模型比较，可以看出简化率为65%的点云模型完全可以反映椅子的特征，同时，点云简化时间大大缩减。(d)图反映的是夹角阈值取2°，K值取15近邻点时，点云简化率在43%时椅子模型，(d)图的模型并不理想，所以通过反复实验，本文方法K最佳取值可以取15，阈值τ取3°。

为了说明基于kd_tree算法和法向量估计的点云数据精简方法的可行性，将法向量估计方法在K值取15，向量夹角阈值取3°时的点云简化模型和包围盒算法点云简化模型进行比较。

包围盒简化方法即是将所有点云数据建立成一个长方体包围盒，并根据一定的分割条件将长方体包围盒进行划分，划分成一定数量均匀小包围盒，选取距离小包围盒中心最近的点云数据来取代小包围盒所有点，完成点云数据简化。图3反映包围盒简化方法和法向量估计的点云数据精简方法在相同简化率时模型对比图。

图3(a)图包围盒算法点云简化图对于椅子特征部位的反映并不理想，曲线部分通过点云简化后，变成直线特征，而图3(b)基于法向量估计算法，简化后的点云对于椅子特征部位反映很好，曲线特征明显。

图3 两种算法在相同简化率模型比较

3 结 语

针对三维激光扫描获取的海量点云数据简化工作，基于kd_tree算法和法向量估计的点云数据精简方法是一种能够很好保留研究对象特征的简化算法。通过反复实验，证明该方法切实可行，能够快速高效实现点云数据精简，并对特征信息能够很好保留，保证后续建模模型的精度。同时，点云数据精简精度取决于K的取值以及点云向量夹角阈值τ的选取，对于不同K值以及阈值τ会产生不同精简效果。K值越大，邻近点云数据越多，拟合平面更精确，精度越高，阈值τ选取保证了点云精简率，所以要反复实验选取合适数值。