矩形耐压舱预应力支柱优化设计

陈静，余恩恩，卢骏锋，程远胜

1中国舰船研究设计中心，湖北武汉430064

2华中科技大学船舶与海洋工程学院，湖北武汉430074

0 引 言

因设备布置的需要，加筋板形式的矩形船舶舱室要求具备抵抗内压的能力（简称“矩形耐压舱”）。而非圆形的结构形式导致这种耐压结构的强度要求难以得到满足，因此有必要采取有效的措施加强相应结构，降低板架弯曲应力水平。高上地等［1］提出了矩形耐压舱角隅结构形状优化与拓扑优化方法，可有效降低角隅区域的应力集中程度。陈杨科等［2］提出了矩形耐压舱内部平台和支柱结构优化设计方法，通过合理确定内部平台的垂向位置、支柱位置及其尺寸，有效降低了舱室板架的弯曲应力。

预应力（Prestressing force）是在工程实施等过程中引入的一种应力［3］，施加预应力以作为充分利用材料性能的一种方式已被广泛应用于机械制造和建筑结构中。在钢结构中引入预应力能够调整结构的受力状态，降低应力峰值，提高结构或构件的承载力［4］。合理设置预应力的大小可以使预应力的效果达到最佳，预应力的配置优化已成为当前研究的热点之一［5-8］。

目前，预应力结构的应用和优化主要集中在建筑和桥梁领域，较少出现在船舶结构设计中。为此，本文拟针对船舶内压下矩形耐压舱结构，进行内部支柱预应力配置优化设计，以及支柱结构布局与预应力配置的共同优化，期望更为高效地利用矩形耐压舱内部支柱结构，以有效降低顶甲板结构的最大弯曲应力。

1 内部支柱预应力设置优化设计

1.1 有限元模型及预应力支柱

本文采用文献［2］中的内压下矩形耐压舱简化有限元模型进行应力分析，局部模型与各结构说明如图1（a）所示。图1（a）中的模型主要参数如下：耐压舱在船长方向长12 m，船宽方向宽9 m，型深方向高9 m，双层底高1.5 m，所有桁材间距均为750 mm。其中，支柱截面尺寸为ϕ200 mm×20 mm ，分布形式如图1（b）所示。支柱位于龙骨（甲板平台纵桁）与实肋板（甲板平台横梁）的交叉处，共18根。模型中，舱壁板及其桁材腹板采用壳单元Shell 181模拟，桁材面板采用梁单元Beam 188模拟，支柱采用Pipe16单元模拟。整体有限元模型网格尺寸大小为400 mm。所有结构材料的力学性能相同，材料弹性模量E=210 GPa，泊松比μ=0.3。

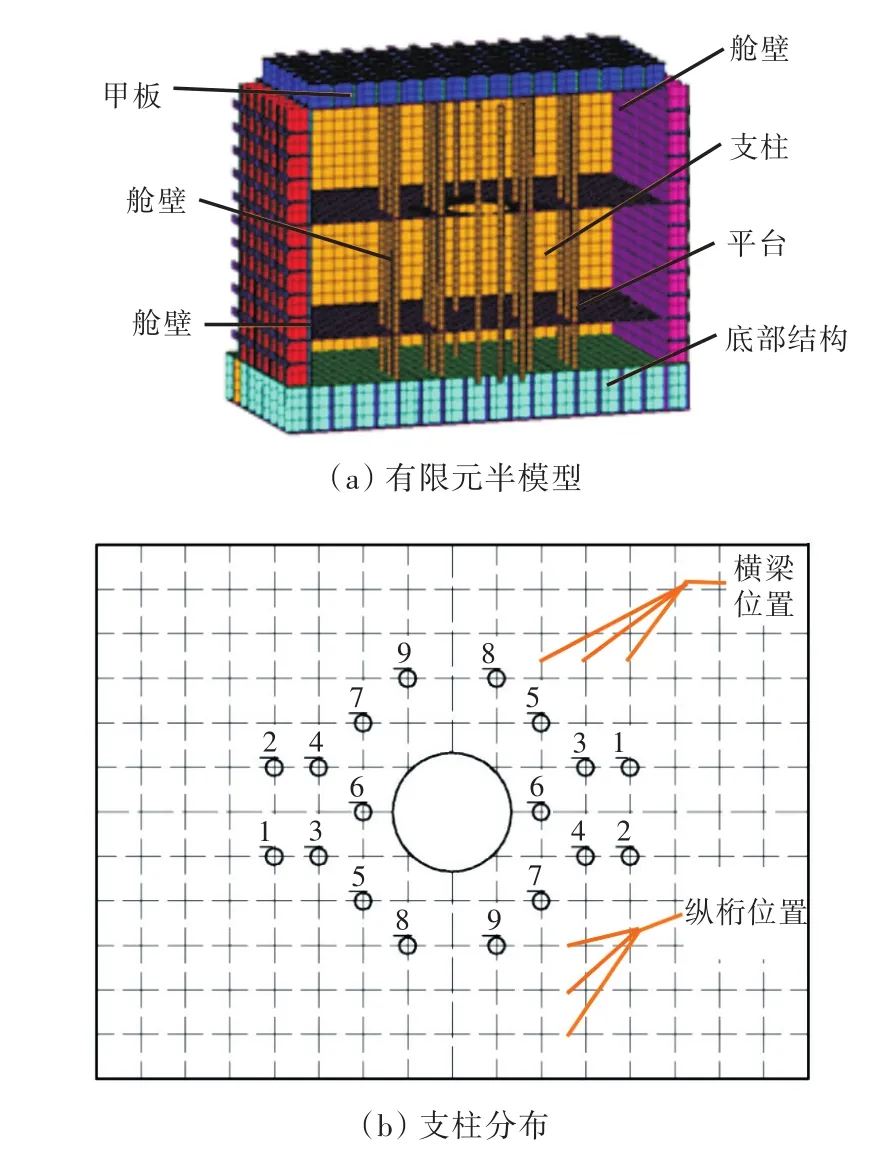
图1 模型结构Fig.1 Model structure

文献［2］采用优化方法获得了18根支柱的合理布置设计方案，该方案使得矩形耐压舱顶甲板板架的最大弯曲应力达到最小。尽管优化得到的是支柱最佳设计方案，但最优支柱方案各个支柱间的应力分布并不均衡，且相对于支柱应力许用值存在一定的裕度。各支柱的应力大小如表1（表中支柱编号见图1（b））所示。由于支柱的应力大小受外载荷的单独影响，为被动响应状态，故无法在不改变其结构形式的情况下使其应力增大。本文考虑采用对支柱施加预应力的方式来使耐压舱顶甲板在无载荷的作用下便存在初始反变形和预应力，即通过充分利用各支柱的应力裕度和预应力调节支柱应力的分布状况，达到进一步降低顶甲板弯曲应力值的目的。

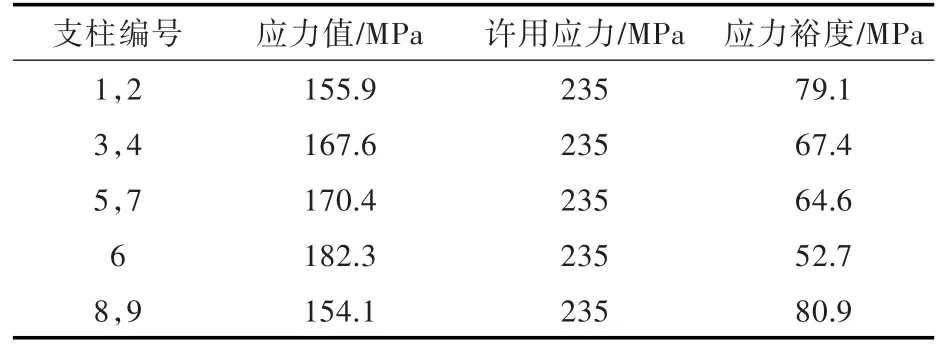
表1 各个支柱的应力状态Table 1 Stress status of each pillar

1.2 优化数学模型

为了验证预应力支柱的有效性，本文保持文献［2］中的原始最优支柱结构形式不变，仅给每根支柱施加初始预应力，优化对象为每根支柱的预应力大小，优化目标仍为顶甲板桁材最大弯曲应力极小化。根据问题描述，建立支柱预应力配置优化数学模型如下：

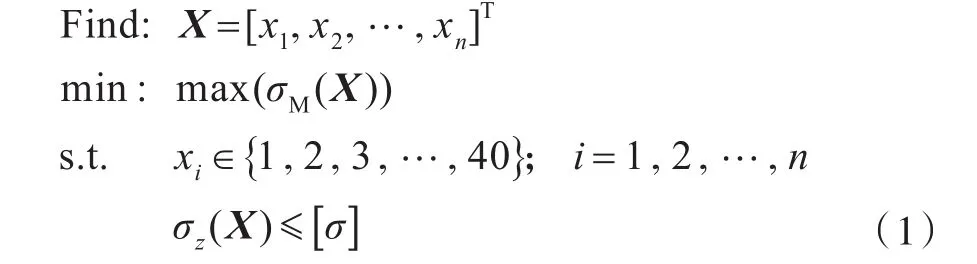
式中：X为预应力配置方案，取个数n=9；xi为单根支柱的预应力大小，预应力大小可取40个离散值，分别用编号 1，2，3，…，40表示，取值范围在-20～85 MPa之间；σz(X)为外载荷下的支柱最大应力，MPa；[σ]为支柱许用应力值，本文设为235 MPa；σM(X)为顶甲板桁材结构最大弯曲应力，MPa。

采用遗传算法［9］求解该优化数学模型，其中xi即为单个基因，xi的组合即为染色体，预应力组合下的甲板弯曲应力即为适应度目标值。对支柱应力许用值约束条件的处理方式，采用罚函数法对支柱应力约束条件进行处理（即不满足约束条件时赋值为较大的目标值），遗传算法选择概率为0.9，采用轮盘赌选择法，交叉概率为0.8，采用多点交叉法，变异概率为0.01，采用实值变异法。遗传算法种群个体数设置为500，最大代数设置为50代。考虑到求解可能提前收敛，为避免浪费不必要的计算时间，终止收敛条件设置为连续8代最优解相同或者达到最大代数。

具体实现为利用Matlab软件调用ANSYS软件，在Matlab中依据谢菲尔德遗传算法工具箱［10］编写优化主控程序，ANSYS软件则作为仿真工具计算有限元模型，获得目标函数和约束函数应力结果后返回至Matlab中。

1.3 预应力支柱优化结果分析

针对给定的支柱布局方案，优化求解各个支柱的最优预应力取值。优化结果如表2所示（表中支柱编号见图1（b）），其中预应力为正，表示支柱承受拉应力，为负则表示支柱承受压应力。

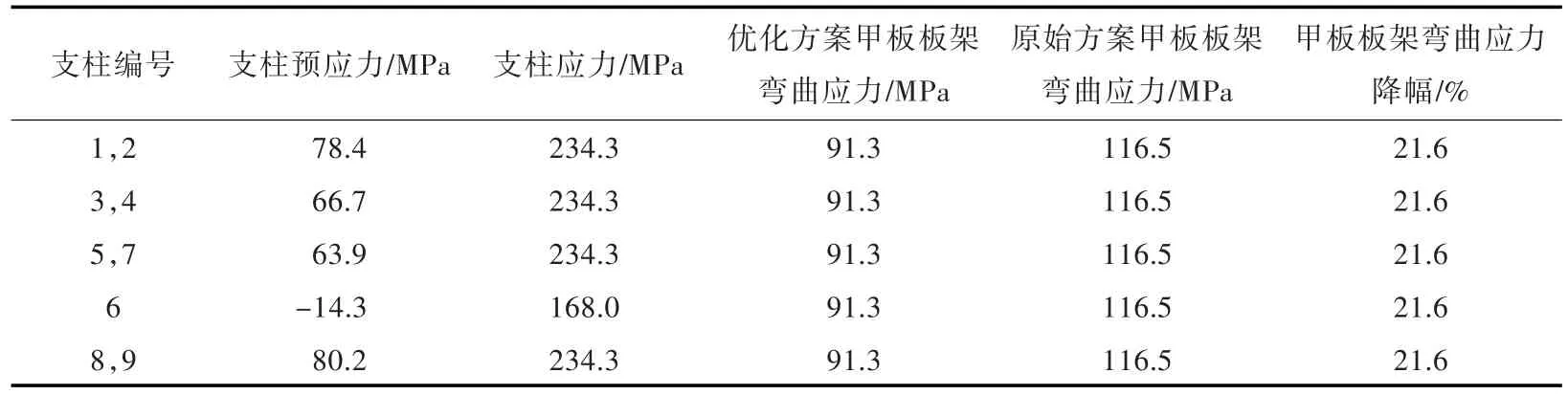
表2 预应力支柱优化结果Table 2 Optimization results of prestressed pillars

表2中结果表明，预应力支柱的设置可有效降低甲板结构的弯曲应力，降幅达21.6%，优化效果较为显著。设置预应力之后，各个支柱的应力状况趋于相同，且均达到了许用值，也即达到了充分利用所有支柱结构材料的目的。

2 内部支柱布置与预应力设置优化设计

2.1 优化数学模型

文献［2］中的支柱布置是基于支柱无预应力状态下优化得到的最佳组合方案。本文中的支柱在引入预应力之后，能使顶甲板桁材的最大弯曲应力进一步降低，该状态下的支柱应力由初始预应力和由外载荷引起的应力这2部分构成，因此支柱在引入预应力后，文献［2］中的最佳支柱布置方案并不一定是预应力状态下的最佳布置方案。为进一步降低顶甲板桁材的最大弯曲应力，本文同时将支柱布置位置与支柱预应力大小作为设计变量，而支柱根数、其他约束条件和目标函数等则保持不变。

依据优化问题描述，建立支柱布置与预应力设置优化设计数学模型如下：

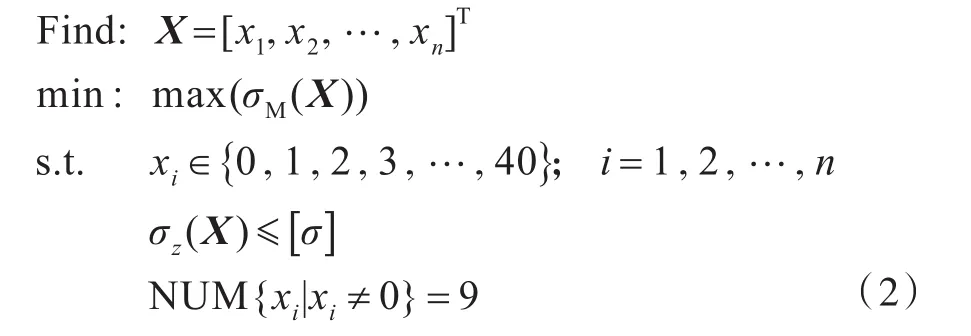
式中：n参照文献［2］取为17；xi为某个可设位置处的支柱设计变量，取值对应于该位置处是否设置支柱以及有支柱下的预应力大小，分别用编号0，1，2，3，…，40 表示，其中0代表此处不设置支柱，其他编号则代表设置支柱并且其取值分别对应于不同的预应力大小，取值范围在-20～85 MPa之间；约束条件NUM{xi|xi≠0}=9表示要求总共9个位置设置支柱。

对比1.2节中的优化数学模型，本节优化数学模型中变量的取值仅增加1个，但变量个数增加了近1倍，优化数学模型的空间复杂度呈指数型快速增长。因此，在采用遗传算法进行优化求解的过程中，需要相应增加种群个数以及延后终止收敛条件，以适应空间复杂度较高的优化问题，从而使得求解得到的最优解具备相对较高的可靠性。所以将求解该优化数学模型的遗传算法中的种群个体数增加为1 000，最大代数增加为70代，终止收敛条件为连续8代最优解相同或者达到最大代数，其他遗传算法参数与1.2节中相同。

2.2 支柱优化结果分析

由遗传算法求解得到的最优支柱布置位置以及布置位置方案如图2所示，各支柱的预应力大小配置如表3（表中支柱编号见图2）所示。

对比图2与图1（b）可知，新的支柱布置方案相比于原方案只有6号支柱发生了改变，由原来的靠近中心区域变为了远离中心区域。对比表2中的甲板板架最大弯曲应力值（表2中的支柱应力）结果发现，新方案的应力值更低，上节的优化设计仅改变了支柱位置而没有将支柱尺寸作为设计变量，即结构重量未发生改变。可以认为，新的优化方案要优于原支柱布置方案下的最佳预应力配置方案，优化效果非常显著，其在原最优结果的基础上仍有16.0%的优化效果。

图2 支柱分布与编号说明Fig.2 Pillar distribution and numbering instructions

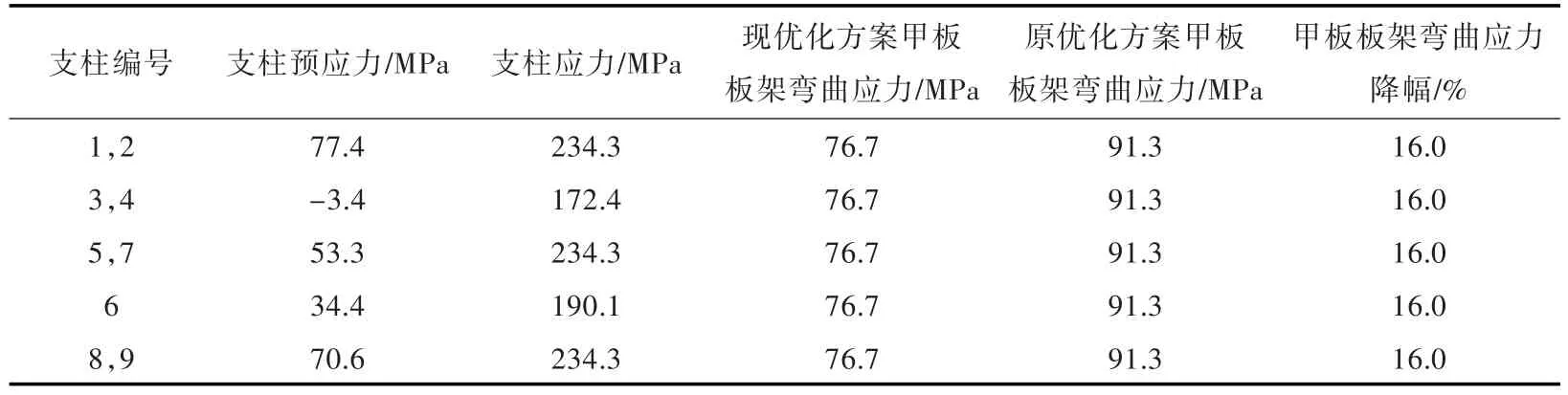
表3 新优化方案下预应力支柱优化结果Table 3 Optimization results of prestressed-pillars under the new optimization scheme

顶甲板桁材面板弯曲应力分布状态如图3所示，从中可以看出最大拉应力与最大压应力接近相等。

图3 甲板桁材面板弯曲应力云图Fig.3 Bending stress contours of deck girders'panels

通过对比预应力支柱优化结果，从支柱布置位置的变化可以看出，预应力支柱的引入会改变支柱最优布置方案。

观察比较各根支柱的应力水平状态，发现施加预应力后各支柱的应力均较大，部分支柱的应力值甚至达到了应力许用临界值，即部分支柱的结构材料得到了完全利用，其他支柱材料也得到了较充分的利用。由此可见，新的支柱布置和预应力设置方案显然更值得采纳。

2.3 支柱截面尺寸优化分析

根据2.2节中得到的最优解，发现尽管大部分支柱的应力都达到了应力许用值，但还是存在部分支柱的应力未到达其许用值、结构材料未充分利用的问题。已有的优化结果意味着当前的预应力状态是顶甲板桁材最大弯曲应力最小化的最佳设置，即不可能通过调整支柱预应力状态来降低目标函数值。若改变当前某根支柱的预应力，虽然可以改变支柱的应力状态，但会增加顶甲板桁材的最大弯曲应力值。

使顶甲板桁材最大弯曲应力达到最小的直接原因并不是各根支柱的预应力大小，而是各根支柱对顶甲板提供的反力，所有支柱反力的最佳组合将使得顶甲板桁材的最大弯曲应力达到最小。若要求保持顶甲板桁材的最大弯曲应力值不发生变化，本质上不应该改变各根支柱所提供的反力。

支柱反力由2部分构成：一部分是由外载荷引起；另一部分是由初始预应力决定。其中，由外载荷引起的支柱反力为被动响应，无法人为决定，但初始预应力却可以由人为决定。若要求支柱反力不变，则当由外载荷引起的支柱反力发生改变后，可以通过相应改变初始预应力来使支柱反力不变。

现存在着部分支柱应力未达到其应力许用值的情况，而通过采用减小支柱截面尺寸的方式则可达到增大支柱应力的目的，同时通过调整预应力大小，还可保持支柱反力大小不变。由于支柱反力为已知常数，应力许用值也为常数，故根据支柱反力与支柱应力和截面面积的关系，便可确定最小的支柱截面面积，然后再根据最小截面面积选择支柱截面型号，即可达到支柱结构材料最少的目标。

3 结 论

本文通过对内压下矩形耐压舱支柱结构进行预应力优化研究，对支柱布置位置和预应力共同进行优化，得到以下结论：

1）矩形耐压舱合理设置预应力支柱，可以更加有效地利用支柱材料，降低顶甲板桁材的最大弯曲应力。本文在文献［2］中最优布置方案（支柱无预应力）的基础上，不改变结构形式，不增加结构重量，通过设置并优化支柱预应力大小，将顶甲板桁材最大弯曲应力降低了21.6%。

2）矩形耐压舱内部支柱在引入预应力后，最佳支柱布置位置相对于无预应力支柱的布置位置会发生改变，存在着更为合理的支柱布置位置和相应的预应力大小设置。本文在支柱数量和尺寸不变的前提下，通过同时优化支柱布置位置和预应力大小设置，使得顶甲板桁材的最大弯曲应力相比于仅优化预应力设置得到的最优方案（此时支柱布置位置为文献［2］中给出的布置方案）下的顶甲板桁材最大弯曲应力，又进一步降低了16.0%。

3）可以依据最优方案下的支柱反力、预应力和应力许用值，合理确定支柱截面尺寸。