构建函数探寻不等式求证思路——以数学问题为例

黄如炎

(福建省闽清教师进修学校 350800)

《普通高中数学课程标准(2017年版)》对逻辑推理素养水平三要求学生“对于新的数学问题，能够提出不同的假设前提，推断结论，形成数学命题；对于较复杂的数学问题，能够通过构建过渡性命题，探索论证的途径，解决问题”[1]．《数学通报》传统栏目“数学问题解答”中的数学问题新颖而有难度，解答机智灵活，精彩纷呈，其中有不少好问题，是培养理性思维，发展高水平逻辑推理素养的难能素材．但许多数学问题没有给出思维过程，有些解答使人感到不够自然，突如其来．问题提的再好，如果问题的解答没有给人任何思维的启迪和思想的感悟，就失去了好问题的教育价值．解决难度较大的数学问题，往往需要提出某个假设或引理，构建函数是提出假设和引理的有效途径之一．本文以数学问题中的不等式为例，通过构建函数，利用函数的导数、图像、单调性、最值、极值等合乎情理地探寻不等式证明思路，以发展学生的逻辑推理素养．

问题1正数a、b、c满足a+2b+3c≤abc，求5a+22b+c最小值(数学问题2080[2])．

原解概要本问题难度较大，引起了许多中数研究者的关注和探究．问题由黄兆麟老师提供，由于他是在赋予a，b，c具体值的情况下设置本问题，可根据已知a、b、c值和均值不等式取等号的条件，对式子进行变形配凑后用均值不等式求出最值[3]．但在外人看来这种变形分拆神秘莫测，知其然不知其所以然．王淼生、杨先义、张青山等老师通过待定系数法、算术平均不等式、加权幂平均不等式等方法进行探究，虽然揭开了黄老师解题的神秘面纱，但都涉及到多元高次方程，求解过程十分艰难[4][5][6]．下面通过构建函数既轻松解决问题又开启新的思维方式．

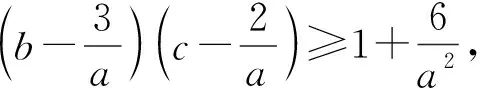
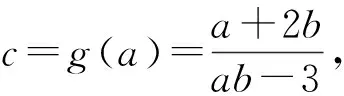
方法提炼对某些多元不等式，可视其中两个元为变量(其它元为常量)构建函数，通过函数的导数、图像与性质解决问题．

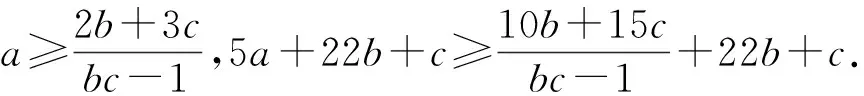
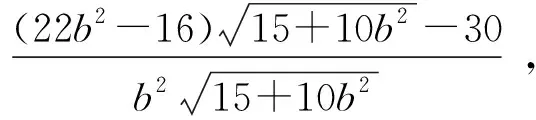
方法提炼对某些关于a，b，c式子的最值，可先构建关于某个字母为自变量的函数f(a)(或f(b),f(c))，求出最值g(b,c)(或g(a,c),g(a,b))，再构建另一字母为自变量函数g(b)(或g(c),g(a))，求出最值h(c)(或h(a),h(b))，再求出h(c)(或h(a),h(b))最值．

问题2若a,b,c>0，aπ+bπ+cπ=3，则ae+be+ce≤3(数学问题2293[7])．

原解要点直接引入函数f(x)=exπ-πxe，此函数是如何构建的呢？

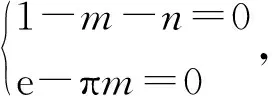
方法提炼对某些多元对称不等式，可根据不等式结构特征，利用不等式等号成立时函数取得极值探寻不等式g(a)≥h(a)，即构造函数f(x)=g(x)-h(x)解决问题，此方法比利用切线寻找函数的一次估计式更具有一般性．

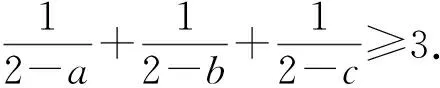
(数学问题2329[8])

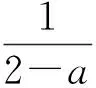
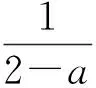
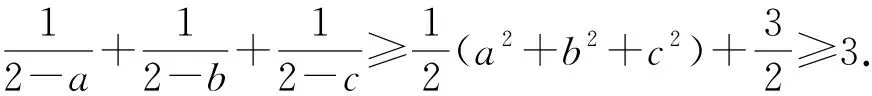
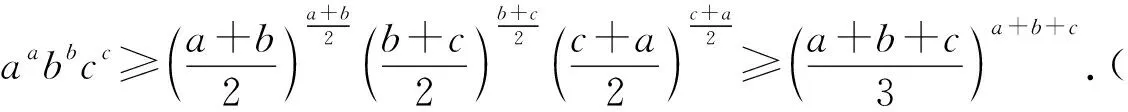
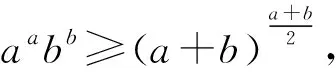
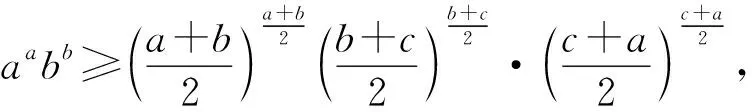
所以f(x)在(0，+∞)上递增，从而

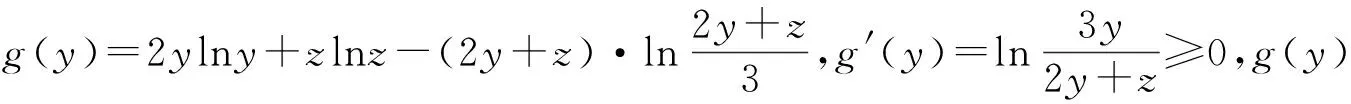
方法提炼对某些关于a，b，c对称的不等式f(a,b,c)≥0(或f(a,b,c)≤0)，不妨设a≥b≥c，先构建关于a的函数f(a,b,c)，证明f(a,b,c)具有单调性后得到f(a,b,c)≥f(b,b,c)(或f(a,b,c)≤f(b,b,c))，再构建关于b的函数g(b,c)=f(b,b,c)，证明g(b,c)具有单调性后得g(b,c)≥g(c,c)=0(或g(b,c)≤g(c,c)=0)．

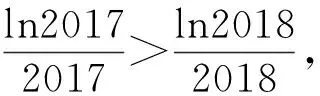
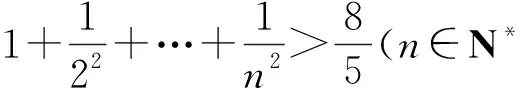
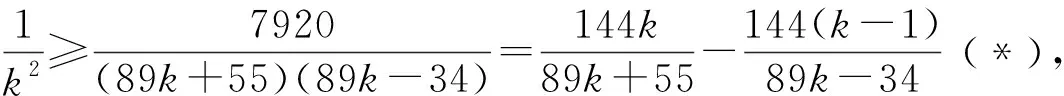
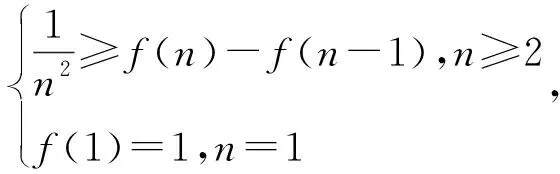
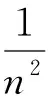
方法提炼对某些不可求和数列{an}前n项和的不等式，可构建函数f(n)使a1=f(1),an≥f(n)-f(n-1)(或an≤f(n)-f(n-1))，n≥2．

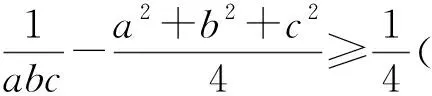
原解要点通过变形、配凑后用5元算术—几何平均不等式证明．也可构建函数证明如下．

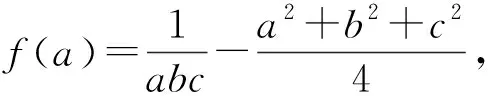
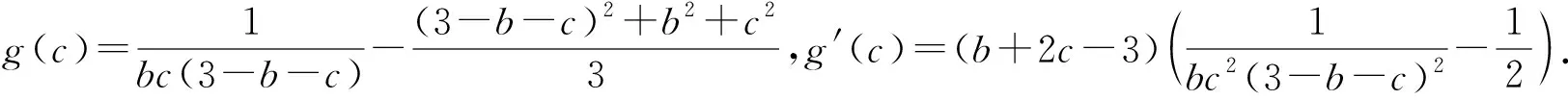
所以g′(c)≤0，g(c)在(0,3)上递减，故

构建函数

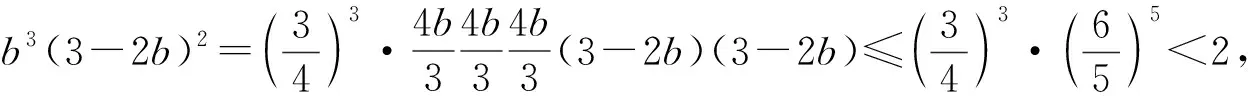
由上可见，有些难度较大的不等式(最值)问题，表面看似与函数无关但背后往往蕴藏着某个函数，如能揭示所隐含的函数，通过研究函数的性质与图像可化难为易，其优点无需证明不等式所用的较强技巧和超出中学范围的不等式公式．此类不等式(最值)问题不仅在《数学通报》的数学问题中频频出现，在各类竞赛题和近年高考压轴题中也时有出现，学生对此不知所措，束手无策，应引起教师教学上的重视．构建函数探寻不等式(最值)求证(解)思路的关键在于根据不等式结构特征，或将不等式变形转化后构建以某个量为自变量的函数，通过研究函数的单调性、最值、极值、切线和图像后解决问题．构建函数在三角、数列、解析几何、立体几何、函数等问题中有着同样的运用，限于篇幅不一一列举．