基于SAT的分离制造攻击方法
刘佳琳,陆 昆,严昌浩,周 海,周 电,曾 璇
(复旦大学 专用集成电路与系统国家重点实验室,上海 201203)
目前,集成电路(Integrated Circuit, IC)在人们日常生活和工作中无处不在.随着集成电路的发展,人们对知识产权保护日益重视、安全意识水平不断提高,芯片设计的安全性得到越来越广泛关注.近几年来,在芯片硬件安全领域,不断有学者提出新的攻击和防御算法.
分离制造作为一种保护芯片设计版图的安全手段被提出,引发了广大学者的研究兴趣.对分离制造的安全性以及对其进行攻击的难易、成本等问题的研究具有重要意义.
1 背景介绍
随着集成电路工艺节点迈向纳米尺度,集成电路产业维持最先进代工厂的成本非常高昂[1].越来越多的设计公司将其芯片制造外包给专门的芯片代工厂代为生产.集成电路生产流程的全球化节省了昂贵生产设备的维护成本,但却可能引入硬件安全漏洞[2].逆向工程[3]、IP盗版、非法过量生产和硬件木马插入[4]等攻击可发生在供应链的任何一环,这些安全问题每年给半导体行业造成数十亿美元的损失[5].
美国情报高级研究计划局(Intelligence Advanced Research Projects Activity, IARPA)提出了分离制造技术[6]作为抵挡这些攻击的防御手段.设计公司将设计出来的最终结果,即准备流片的GDS版图文件分为两部分: 前端部分(Front-End-Of-Line, FEOL)或称下层部分由晶体管和底部密集的金属层组成,这一部分通常具有比较小的线宽而必需采用先进工艺生产;后端部分(Back-End-Of-Line, BEOL)或称上层部分是由顶部金属层构成,它具有相对较大的线宽,无需特别先进的制造工艺,可以由规模较小、工艺落后但受信任的芯片代工厂生产[7].Hill等[8]实现了一个1300万晶体管规模的复杂数字集成电路在单一代工厂的标准制造和在不同代工厂的分离制造.
分离制造通常有两种情况[9]: 1) 制造FEOL和BEOL的两个代工厂均是不被信任的,他们制造出的部分芯片需由受信任的集成设备来集成;2) FEOL部分由先进而不受信任的代工厂制造,然后交付至工艺较落后但是受信任的代工厂来完成BEOL部分的制造.设计人员将GDS版图文件分成两部分分别交付给不同的代工厂生产制造,由此增强了芯片的安全性.分离制造使单独一个代工厂失去了对完整芯片的掌控,代工厂在没有完整芯片电路信息的情况下,无法准确定位插入木马的“安全”地点,或是随意盗版生产整个芯片电路[10].在本文中,与大多数研究者一样,着重研究第2种情况.
分离制造的示意图如图1所示.假设多层芯片版图由图1(a)中的粗实线分割开,则BEOL部分位于粗实线上方,FEOL部分位于粗实线下方,分离所产生的切割点可能是通孔(via),例如图1(d)中缺失连线的断点x1、x2、x3处于通孔处且连接至器件的输入引脚,断点y1和y2,处于通孔处且连接至器件的输出引脚.同时,分离所产生的切割点也可能是电路原始引脚(Pin),例如图1(d)中左下角的断点Pin1.分离制造虽然一定程度上加强了芯片的安全性,但是恶意代工厂仍然可以利用一些启发式的算法来恢复整个电路.作为一个攻击者,在制造FEOL部分的代工厂(如图1(b)所示)可以访问工艺库文件,在现有逆向工程工具[3]的帮助下,可获得不完整的门级网表(Incomplete Gate-level Netlist, IGN),该网表丢失了由BEOL决定的一些连线,如图1(d)所示.攻击者的目标就是恢复这些缺失的BEOL连线,以获得完整的电路设计,如图1(c)所示.
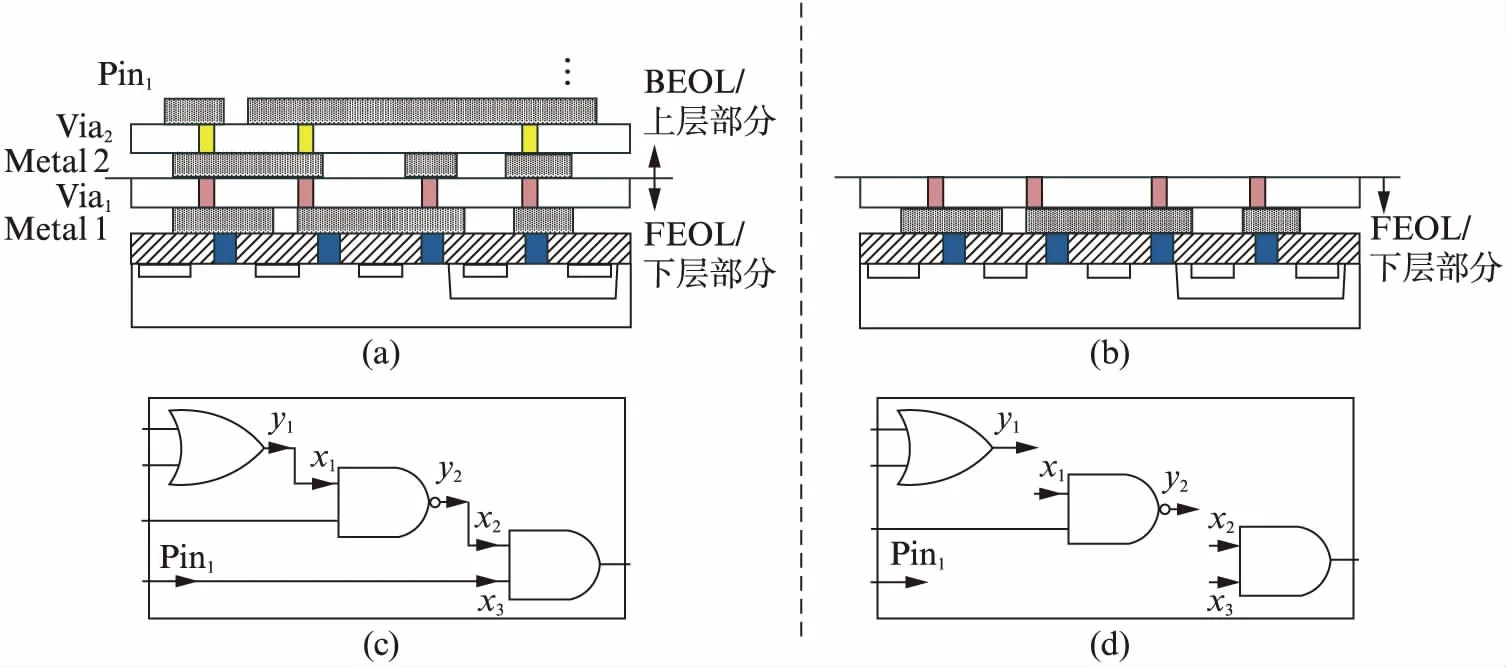
图1 分离制造示意图Fig.1 Demonstration of split manufacturing
针对分离制造的攻击方法,Rajendran等[10]提出了一种启发式的攻击方法,可以正确连接96%的BEOL连线,但他们仅在一个小测例上实现了100%的正确连接.Vaidyanathan等[11]证明,在第一层金属层(Metal 1)进行分离制造可以隐藏所有逻辑门之间的连线,并且这种做法的开销也小到可以忽略,但他们的测试芯片采用130 nm CMOS设计,在更先进的工艺节点下,可制造性设计(Design for Manufacturing, DFM)问题可能导致良率波动极大,因此对低层金属(如第一层金属)的切割应更为慎重.Magãna等[7]研究了不同的邻近攻击以确定每条缺失连线的候选者,并指出仅靠邻近攻击无法恢复整个电路所有连线.Wang等提出的邻近攻击[12]以整体方式综合利用布局、布线阶段的经验信息,并使用网络流模型来推断连接;试验结果表明,基于网络流的攻击仅在c880和c5315 2个电路上得到了100%的连线正确率,其他7个电路均未达到100%[12].从实用的观点来看,只有当恢复出的电路与原始电路完全一样,即对于任何输入向量都能产生相同的输出向量时,才可认为攻击是成功的.换句话说,凡是小于100%的连线正确率,在攻击成功率上都可以看做是零.
Chow等[13-14]提出用与金属端不相连的通孔设计来抵御芯片的逆向工程(如芯片拍照),这种通孔称为假通孔(dummy via),可有效误导逆向工程者认为实际上下断开的金属层之间是相连的,若有t个假通孔,通过精心设计这些假通孔在电路中的摆放位置,可将破解真假通孔问题的复杂度提升至指数复杂度O(2t)[15],其中任何一个判断失误都可能导致整个攻击的失败.而基于SAT的软件攻击算法可不受此类伪装手段的误导,且能保证破解出来的电路功能与原电路完全相同.此外,直接进行逆向工程的成本一般也远远高于基于SAT的软件攻击算法.
本文提出并实现了一种名为SplitSAT的攻击方法来攻击基于分离制造的芯片,针对缺失连线的建模过程,建立了从分离制造攻击到逻辑解密的桥梁.由于该模型引入环路到原始的无环电路中,因此我们采用更先进的CycSAT算法[16],该算法有效地解决了带环电路的布尔可满足性问题(Boolean Satisfiability Problem, 简称SAT问题)求解.在此基础上,利用几何信息为每个待连接的输入点构建候选列表,减少SAT求解空间,极大提高了SplitSAT的求解效率.
2 问题模型定义
分离制造攻击模型中,假设先进而不可信的代工厂制造FEOL部分,可信代工厂制造BEOL部分.前者为攻击者,其目标是利用工艺文件和FEOL信息来试图恢复缺失的BEOL连线.
2.1 基于网络流算法攻击分离制造电路
Wang等[12]提出了一种基于网络流的攻击方法,该方法考虑了源自传统物理设计布局/布线阶段常用的一些基本结论,即物理距离、无环组合逻辑、负载电容约束、悬挂线的方向以及时序约束等.但文献[12]假设攻击者无法获知原始电路的具体功能.如图2所示,文献[12]将不完整的门级网表(图2(a))的连接问题建模为网络流问题(图2(b)),Eoi是从输出点(yi)到输入点(xj)的边集合.通过边(yi,xj)∈Eoi上的流量来推断点yi和点xj之间的连线与否.
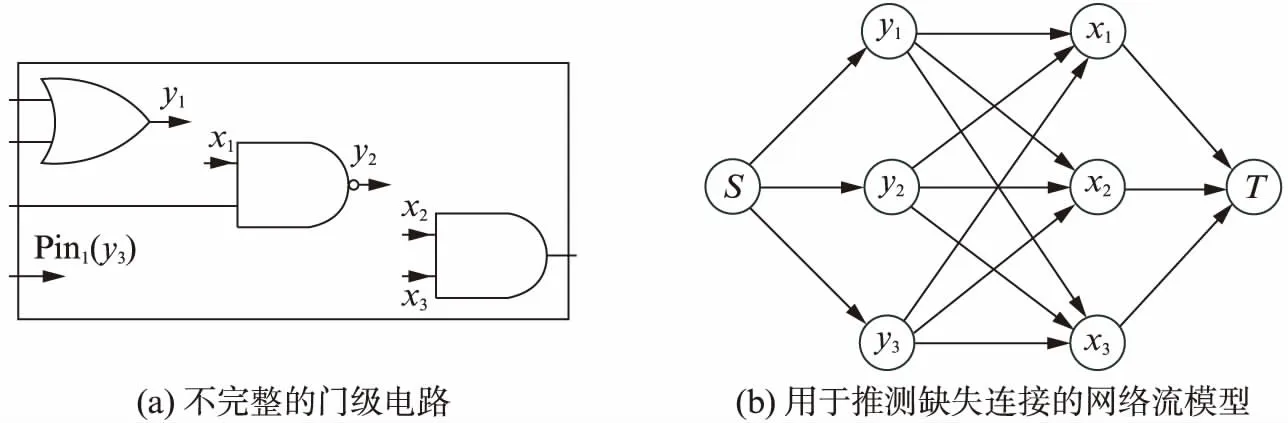
图2 基于网络流的攻击Fig.2 Network-flow based attack
2.2 基于SAT算法攻击逻辑加密电路

图3 逻辑加密示意图Fig.3 Demonstration of logic encryption
抵御芯片硬件攻击的另一组技术称为逻辑加密[17-20].逻辑加密的示意图如图3所示,其主要思想是通过插入额外的门或修改原始IC设计,引入额外的输入,即密钥.当且仅当设置了正确的密钥k*,电路才能正常工作;否则,对于给定的输入,电路将产生与预计不符的错误输出.
Subramanyan等[21]提出了一种基于可满足性问题的攻击逻辑加密电路的算法,他们对每个测试电路分别施以6种逻辑加密算法来形成加密电路,实验结果表明SAT几乎可以全部解密成功.该算法核心步骤是,给加密电路的两个副本施以相同的输入向量,但分别给予不同的、受一定条件约束的密钥,然后检查它们是否产生不同的输出.能够产生不同输出的输入向量称为有分辨力的输入模式(Differentiating Input Patterns, DIP),DIP可以用来排除错误的密钥,并进一步约束接下来所考虑的密钥.图4给出了基于SAT算法攻击逻辑加密电路的示意图.f(x)是原始电路的黑盒布尔函数,给定输入模式x,得到输出为f(x).g(x,k)是逻辑加密电路的布尔函数.
2.3 SplitSAT攻击问题定义
以前,大多数研究工作均假设攻击者无法获得功能正常的目标芯片[10,22-24].在本文中,同Xie等[25]的研究工作一样,放宽Wang等[12]假定原始芯片的输入-输出对不可获得的限制条件,假设攻击者可以获得原始IC的输入-输出对.
事实上,上述假设一般是符合实际情形的.第一,虽然市场上没有目标芯片,但其功能往往可以从公开系列产品的低端型号产品中猜测或获取.因为产品通常是连续的,新一代的功能可以从旧产品中获得.其次,若目标芯片可以直接从市场上买到,直接进行逆向工程的成本一般远远高于基于SAT的软件攻击算法.甚至有些芯片在其金属层中运用了一定的伪装手段以抵御逆向工程,例如,金属层到金属层之间具有间隙的假通孔可以欺骗拍照逆向工程者得到错误的连接[13-15,26],而基于SAT的软件攻击算法可以不受这些欺骗的误导.
基于这一假设,分离制造攻击问题的完整表述如下:
给定分离后的版图布局(FEOL信息)和相应的工艺库以及对原始正确电路的黑盒访问,找到缺失的BEOL连线,使恢复的电路可以完全(100%)像原始电路一样正常工作.
为了解决以上电路连接关系的确认问题,本文采用多路复用器引入模拟加密电路,将恢复电路连线的问题转化为逻辑加密电路的可满足性问题,即将恢复缺失BEOL连线的问题转化为逻辑加密电路密钥求解的问题.
逻辑加密电路中,密钥的作用实际上就是在多种可能性当中选择正确的那一种,例如利用一位密钥选择某个混淆的器件是与非门还是或非门,0代表与非门,1代表或非门.这种机制启发我们用多路选择器来把恢复缺失BEOL连线的问题建模到逻辑解密问题.换句话说,对不完整的FEOL电路用选择器进行模拟加密,将正确的选择信号看做密钥,全部的选择信号即代表一种电路连接,找到了密钥即代表恢复了正确连接.
3 SplitSAT攻击算法
SplitSAT攻击算法采用计算机理论中的可满足性理论进行电路连接关系的建模,以实现电路的恢复.本节将介绍SplitSAT算法对分离制造的攻击流程,使用多路复用器将分离制造攻击问题转化为逻辑解密问题的具体建模方法以及运用几何信息和物理设计工具特点的解空间缩减方法.
3.1 SplitSAT攻击流程
分割层(split layer)的定义: 发生BEOL和FEOL分离的金属层.例如,若设计者选择Metal 5作为分割层,则意味着制造FEOL部分的代工厂无法获得Metal 5及其以上金属层的信息.注意,Via4(即Metal 4和Metal 5之间的通孔层)是攻击者能看到的[12,18].
整个SplitSAT算法的攻击流程如图5(见第700页)所示.先进而不受信任的代工厂即攻击者,从FEOL信息和工艺库开始,首先要逆向出不完整的门级网表,然后使用多路选择器(mux)对缺失连线进行建模,生成逻辑加密电路g(x,k).给定原始电路的黑盒函数f(x),若CycSAT求解出密钥k*,则表示攻击成功,该密钥k*就蕴含了目标电路FEOL部分所缺失的BEOL连线信息.
一旦发生分离制造,就会产生一些金属线的缺失,进而产生攻击者待连接的切割点.如图6(见第700页)所示,假设分割层是Metal 5,那么攻击者需要连接4个切割点: via1,via2,via3,和Pin1.先记录下所有切割点的坐标,然后可将它们分为输入和输出两组,通过追溯每个切割点的路径来判断其所属的集合.一组是输出点集,包括电路的原始输入和中间逻辑门的输出,在图6中,Pin1和via2属于输出点集.另一组是输入点集,包括电路的原始输出和中间逻辑门的输入,这里的via1和via3属于输入点集.
则问题转化为: 对于输入点集中的每一个点,找到其信号来自于哪一个输出点,并进行连线.注意,一个输出点可以连接到许多输入点,而一个输入点只能来自于一个输出点.
3.2 SplitSAT攻击方法的建模
有了所有待连接的点,就可将原分离制造攻击问题建模为逻辑解密问题.每一个输入点,利用多路选择器从所有输出点中选出它自己的源信号,可选到其真实源信的各选择信号值,构成一个局部密钥.所有输入点形成的局部密钥合并则构成整个电路的密钥.
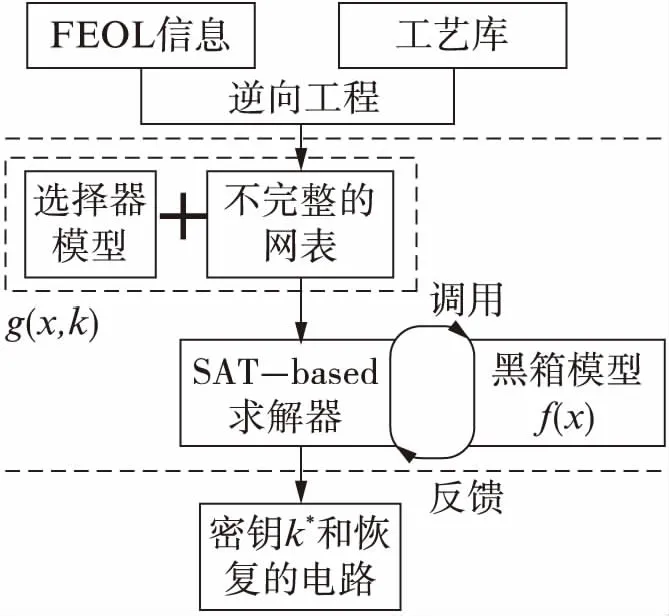
图5 SplitSAT攻击流程图Fig.5 SplitSAT attack flow
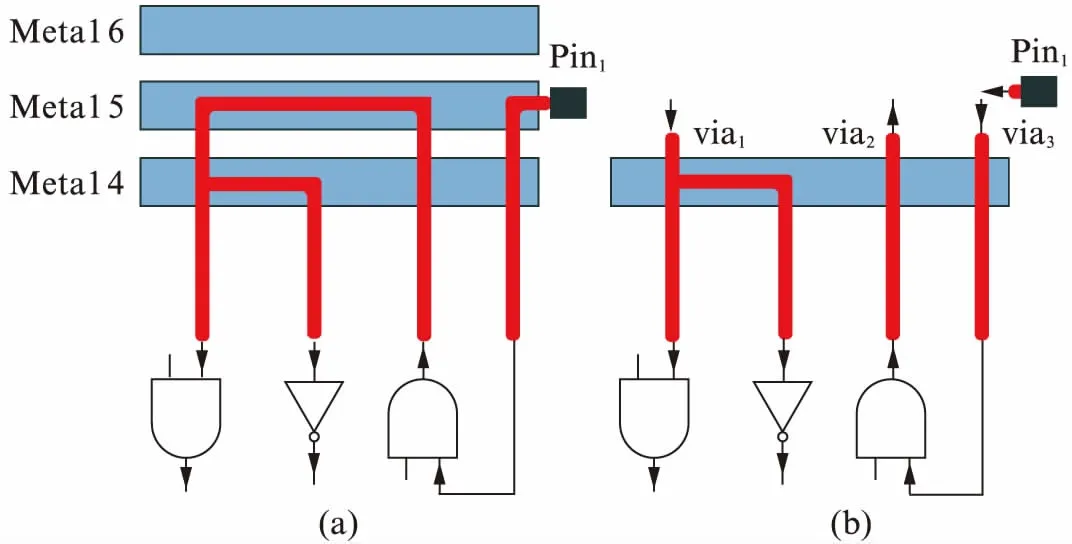
图6 找到待连接点: (a)分离之前;(b)分离之后Fig.6 Find the points to be connected (a) before split and (b) after split
图7给出了一个由分离制造攻击到逻辑解密问题建模的具体例子,其中图7(a)是要实施攻击的代工厂由下层部分信息所得到的不完整电路,绿色虚线表示该电路上层部分的连接信息,攻击者不可见;图7(b)是对应的逻辑加密模型.对于每一个输入点xi,有3个输出点y1、y2和Pin1作为其可能的信号源,因此每个输入点需要2个二路选择器.具体来说,keyinput0在y1和y2之间选择,选择结果为w1,然后keyinput1在w1和Pin1之间选择,最终得到x1.在此示例中,正确的keyinput0和keyinput1的值都是0,即x1形成的局部密钥为00.x2和x3以类似的方式建模,则整个电路的密钥长度为6.对于图7中的电路,正确的密钥是0010x1,其中x表示0和1都可以.
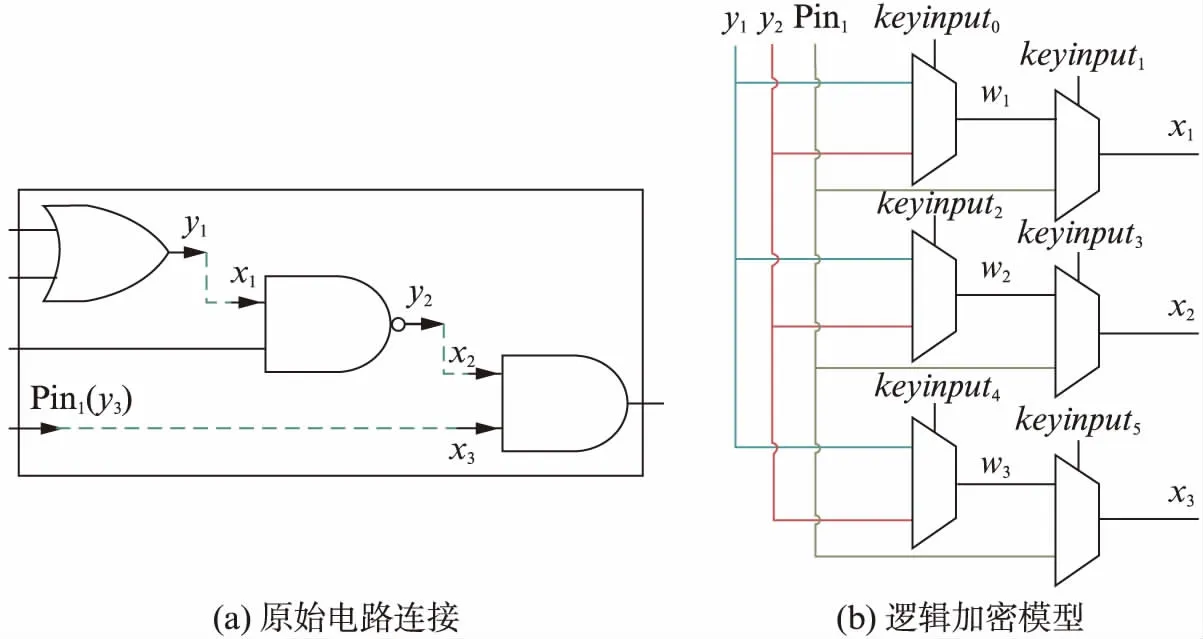
图7 用选择器模拟逻辑加密Fig.7 Using mux to simulate the logic encryption
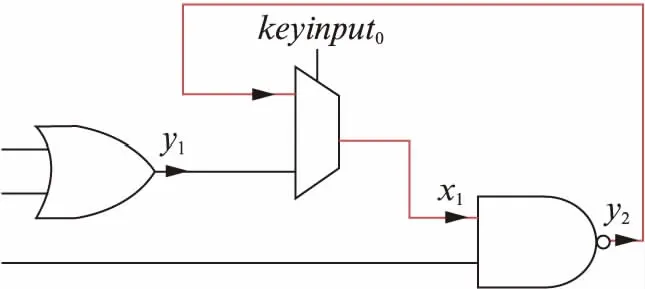
图8 建模时环路的引入Fig.8 Cycle introducing when modeling
在用选择器对缺失连线进行建模的过程中几乎不可避免的会引入环路.如图8所示,输入点x1需要在输出点y1和y2之间进行选择,而y2又依赖于信号x1,因此,形成一个循环.注意,与图7(a)相比,这里为了简明清晰,仅显示了x1的相关部分.
Shamsi等[27]声称基于SAT的算法无法解决循环逻辑加密,即存在反馈环路的电路.事实上,Xie等[25]提出的基于SAT的攻击方法,结果中出现很多“TO(time out occurs at 10 hours)”情况,分析其原因,是传统SAT求解器无法解决带环的电路而导致的失败.
本文引入先进的CycSAT算法[16]来解决环路问题.CycSAT的伪代码在表1中给出,其主要思想是: 找到表示“在密钥k下没有循环(No Cycle, NC)”的情况的合取范式(Conjunctive Normal Form, CNF),并将该CNF加入到原本应用SAT算法时的CNF中去[17].

表1 结构化CycSAT算法伪代码
只要得到正确的密钥k*,使得对于任何输入模式x,都有g(x,k*)≡f(x),就意味着找到了所有缺失的连线,以此复原的电路便能够完全像原始电路一样正常工作.
3.3 解空间缩减
假设现有M个输出点和n个输入点等待连接,如果将所有输出点都视为每个输入点的候选者,则一个输入点的连接关系就需要(M-1)个二路选择器在M个输出点中进行选择,整个电路共需要n(M-1)位的密钥.由于SAT算法可以求解的问题规模有限,减少问题规模可提升可破解芯片的规模.
众所周知,IC通常是通过传统的物理设计(布局、布线)工具设计的[10,12].因此,有理由认为一个引脚不太可能连接到距其太远的引脚,否则,它可能导致高成本或时序收敛问题.基于这个限定条件,可以为每个输入点依据距离,构建一个候选列表,以便从中选择它的信号源,而不是从所有输出列表中选取.这里有两种候选者,即通孔-通孔(via-via)候选者和通孔-引脚(via-pin)候选者.
3.3.1 通孔-通孔(via-via)候选者
对于目标输入点,例如图9(a)中的通孔a,寻找最近的m个输出通孔添加到其候选列表中.为了与布局布线工具兼容,本文选择曼哈顿距离来表示两点之间的距离.在版图布局中,通孔a(p1,q1)和b(p2,q2)之间的距离dab由dab=|p1-p2|+|q1-q2|来表示.如图9(a)所示,对于目标输入点a,如果设置m=2,则b和c同时被添加到a的候选列表中;如果设置m=1,则a的候选列表将只含有c而不包括b,因为dac小于dab.使用合理的参数m,实际连接到目标输入点的输出点将被包含在相应的候选列表中,否则若候选列表中不包含正确解,SAT求解器将无法给出正确密钥.
3.3.2 通孔-引脚(via-pin)候选者
另一方面,版图布局周围的原始引脚也可能直接连接到芯片内部较远的某个通孔,因此它们之间的距离可能相对较大,也应将它们添加到对应的候选列表中.出于这种考虑,将整个版图布局划分为3×3的网格,如图9(b)所示.如果目标输入点位于布局的中心区域Z中,例如通孔b,则将版图布局四周的所有引脚都加入其候选列表.如果目标输入点位于4个角区C1、C2、C3或C4中,那么将版图该角落对应的2个1/2边缘上的引脚加入其候选列表,例如,如图9(b)中左上角外围红色虚线所示,上边界的左半部分和左边界的上半部分含有的引脚,将被加入区域C1中的通孔a的候选列表.对于其他4个区域的目标输入点,其候选列表将包括相应位置整条边界上的引脚,例如,图9(b)中右边界上的8个引脚都将被加入目标点c的候选列表,由蓝色表示.

图9 候选点(a) 通孔的通孔候选点和(b) 通孔的引脚候选点Fig.9 Candidates (a) via-candidates for vias and (b) pin-candidates for vias

表2 SplitSAT算法伪代码
通过上述两个候选者原则,可以构建所有目标输入点的候选列表,这样减少了问题的规模,有利于基于CycSAT的算法来求解.对于一个攻击问题,首先尝试使用完整模型的原始CycSAT;如果规模太大导致求解失败,则尝试使用via-via候选列表方法减少问题规模后求解;最后,同时考虑via-via和via-pin候选者,进行求解.表2给出了具有解空间缩减方法的整个过程的伪代码.一旦得到密钥k*,就相当于获得了缺失的BEOL连接,即恢复出了目标攻击电路.
4 结果及分析
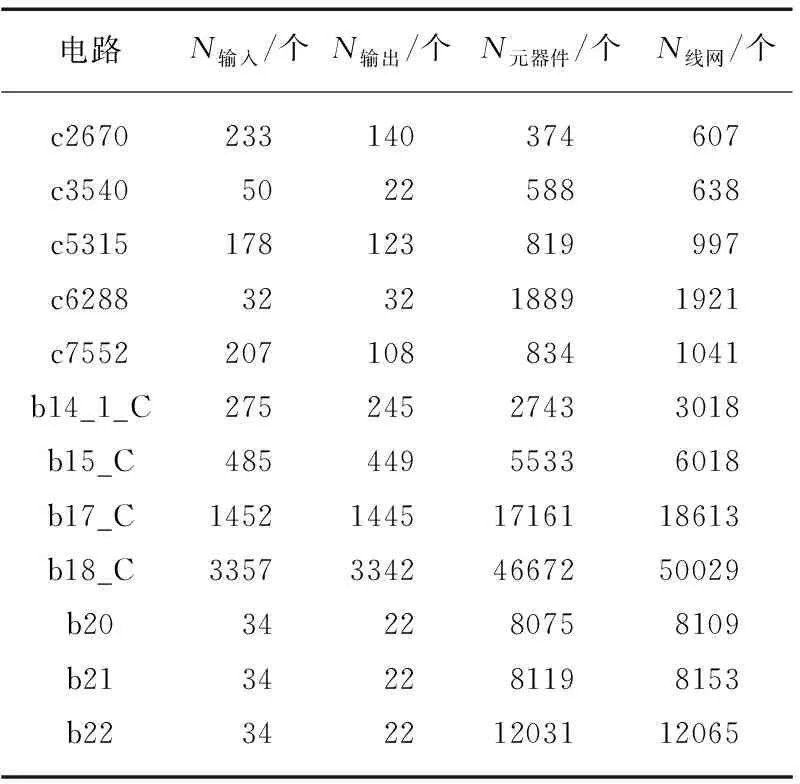
表3 原始测试电路信息
使用ISCAS-85标准测试算例中最大的5个电路和ITC-99标准测试算例中最大的7个电路来评估SplitSAT对分离制造的攻击,这些测例与文献[28]中完全相同.表3中列出了原始电路基本信息,第1列为电路名称,其余列分别为相应电路的输入、输出、器件和线网的数量.这些电路由Synopsys Design Compiler工具综合,原始的版图布局是使用Nangate 45nm开放式单元库(http:∥www.nangate.com/?pageid=2325)和Cadence SoC Encounter工具生成的.算法由C++实现,所有试验的运行环境为Intel Xeon X5650 CPU,主频为2.67GHz,内存为48GB.
Wang等[12]通过计算所能恢复的正确连线的数量来评估其攻击模型的有效性,因为假设攻击者总是试图恢复尽可能多的连线.但攻击者的最终目标是获得一个与原始设计完全一样的电路,因此,本文将100%正确率作为攻击有效性的评估标准.换句话说,如果可以从FEOL信息中完全复原出功能正常的原始电路,则认为攻击是成功的,否则就是攻击失败.
表4是SplitSAT与基于网络流的邻近攻击[1]的试验结果对比,所有试验所处设备环境相同.第1列表示不同电路,其余6列表示对应电路的分割层.“Δ”表示电路没有相应的金属层.一般而言,对于同一个电路,分离发生的金属层数越低,切割到的连线越多,产生的断点数也越多,问题规模越大,求解越困难.
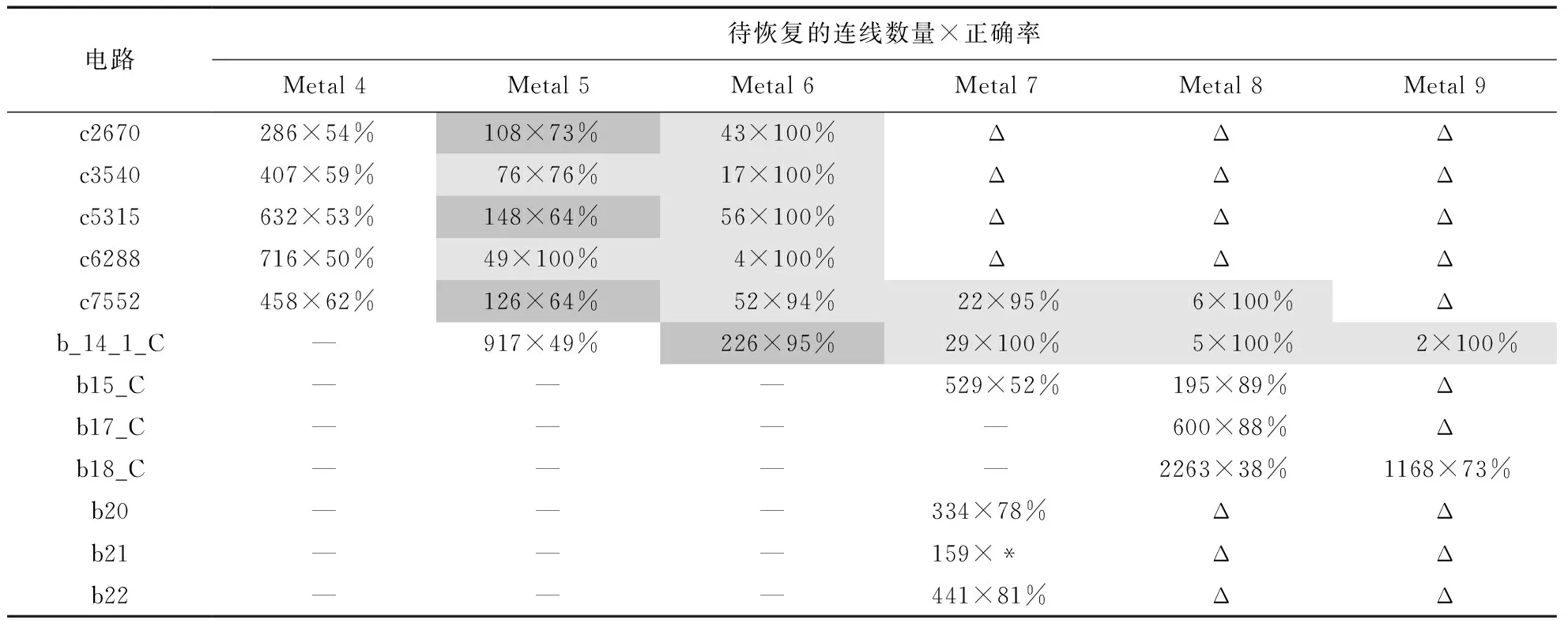
表4 SplitSAT与基于网络流的攻击结果对比
注: “—”表示未进行实验;“*”表示62h仍未得出结果;“Δ”表示电路没有该层金属层.
表4内数据表示该测例缺失的连线数量以及文献[1]网络流攻击的连线正确率.缺失的连线数量可以大致衡量问题的规模.灰色阴影表示SplitSAT可以100%攻击成功,其中: 浅灰色表示使用CycSAT成功破解,深灰色表示进一步采用文章3.3节中提出的经验式候选列表方法成功破解.
由表4可以看出,网络流攻击[12]能100%破解的测例,SplitSAT均能100%破解;对于网络流攻击[12]未能100%破解的测例,SplitSAT仍能部分成功破解.事实上,网络流攻击[12]能100%破解的测例中缺失连线数最大为56(c5315在Metal 6分离);而SplitSAT最大可完全破解缺失226条连线的测例(b_14_1_C在Metal 6分离),能破解问题规模大约是网络流攻击[12]的4倍.SplitSAT算法中,仅使用CycSAT成功破解的缺失连线数最大为76,而采用文章3.3节中提出的解空间缩减方法后,将缺失连线数扩展至最大226条,该结果证实了解空间缩减方法的有效性.
表5列出了本文提出的SplitSAT攻击方法能100%破解的各测例与Wang等基于网络流的邻近攻击方法[12]的详细数据对比.第1列表示每个电路以及对应的分割层;第2~4列为网络流攻击方法[12]的结果,包括分离过程中产生的总切割点数,运行时间和恢复连线的正确率;最后6列是SplitSAT方法的攻击结果,包括切割到的引脚数,通孔数量,CNF的规模,算法运行的迭代次数和时间.特别地是,当SplitSAT攻击成功时,其连线正确率为100%.
Wang等基于网络流的邻近攻击[12]和本文提出SplitSAT攻击的算法复杂度是不同的.基于网络流的邻近攻击[12]中,在切割产生的输出点集和输入点集之间模拟建立最大流网络,可在多项式时间内求解,当该网络有u个点和v个有向边时,最坏时间复杂度为O(uv2);而本文提出的基于SAT问题求解方法的复杂度是NP-完全问题.对于芯片攻击而言,芯片攻击的成功率是第一位考虑的,本文中将破解所需时间放在相对次要的地位.
由表5结果可以看到,测例电路c2670在Metal 5分离时,基于网络流的邻近攻击虽然耗时只有0.8s,但连接正确率仅为73%,这对于破解电路这一最终目标而言,意义不大.而SplitSAT虽然耗时36.82s,却可以100%恢复连线,完全破解.针对部分问题规模很小的测例,SplitSAT的效率可能更高,例如电路c3540在Metal 6分离时,仅缺失17条连线,SplitSAT仅需要1.16s就能100%破解,比基于网络流的邻近攻击(5.28s)耗时更短.

表5 基于网络流的方法与SplitSAT攻击细节对比
注: “—”表示该测例太小以至于无需使用选择器模型.
除了分离产生的断点数量之外,电路本身的规模也会影响运行时间,电路规模越大,恢复原始设计所需要的时间则越长.例如,同样以Metal 5为分割层,SplitSAT攻击c2670电路需要36.82s,而攻击c7552电路则需要282.35s,这两个测例切割点的数目相当,c2670引脚和通孔数为198个(96+102),c7552引脚和通孔数208个(93+115),但c7552电路规模大于c2670电路.当原始电路本身规模较大时,CycSAT求解器必须花费更多的时间来验证输入-输出对,且CNF更长,所以时间开销也更大.对于切割层位置太低或电路规模太大的情况,SpliSAT的能力仍然受到一定程度的限制,未来还有待进一步研究.
5 结 论
针对分离制造攻击问题,本文提出了基于SAT算法的攻击方法SplitSAT,引入先进的CycSAT算法处理建模过程中引入环路的问题,利用物理信息构建切割点的候选列表的方法来减少问题规模.与最新基于网络流的邻近攻击[12]的结果相比,SplitSAT可以在更多、更大规模的测例中实现100%的正确率.

