数形结合与空间观念在初中数学解题中的应用
黄玉梅


摘要:数学是一门比较抽象的学科,要激发并维持学生的学习兴趣,必须重视学习方法的研究与渗透。常用的数学思想方法包括很多,这里重点谈的是数形结合思想与空间观念的应用。所谓数形结合思想,就是指根据数与形之间的一一对应关系,把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来,通过“以形助数”或“以数解形”,即通过抽象思维与形象思维的结合,使复杂问题简单化,抽象问题具体化,优化解题途径的思想。而空间观念是几何课程改革的一个课程核心的概念,《数学课程标准》描述了空间观念的主要表现,其中包括“能够由实物的形状想象出几何图形,由几何图形想象出实物的形状,进行几何体与其三视图、展开图之间的转化”。这是一个包括观察、想象、比较、综合、抽象分析,不断由低到高向前发展的认识客观事物的过程,是建立在对周围环境直接感知基础上的、对空间与平面相互关系的理解和把握。
关键词:数形结合;空间观念;中考;效率
中图分类号:G633.6 文献标识码:A文章编号:1992-7711(2019)24-060-2
因为我多年从事初三数学的教学,因此深刻感受到数学思想方法的重要性。毕业班的学习特点就是时间紧,任务重。若要打好中考这场硬仗决不能强攻,只能智取。作为比较抽象的数学,如果要激发并让学生特别是九年级的学生保持对数学的学习兴趣,那么经常提炼归纳各种数学思想方法尤为重要。在各类思想方法中,我觉得数形结合思想与空间意识的运用最能给学生解题带来惊喜。所谓数形结合思想,就是指根据数与形之间的一一对应关系,把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来,通过“以形助数”或“以数解形”,即通过抽象思维与形象思维的结合,使复杂问题简单化,抽象问题具体化,优化解题途径的思想。数形结合思想是初中课本中的基本的数学思想,在初中数学教学和解题中起着十分重要的作用。而空间观念是几何课程改革的一个课程核心的概念,《数学课程标准》描述了空间观念的主要表现,其中包括“能够由实物的形状想象出几何图形,由几何图形想象出实物的形状,进行几何体与其三视图、展开图之间的转化”。这是一个包括观察、想象、比较、综合、抽象分析,不断由低到高向前发展的认识客观事物的过程,是建立在对周围环境直接感知基础上的、对空间与平面相互关系的理解和把握。数形结合思想与空间意识是相辅相成的,它们有密切的关系,在初中数学解题中可以为我们带来莫大的便利。
首先谈谈如何利用数形结合思想去解决常见数学问题。
华罗庚说过:“数无形时少直觉,形少数时难入微,数与形,本是相倚依,焉能分作两边飞。”由于数和形是一种对应,有些数量比较抽象,我们难以把握,而形具有形象、直观的优点,能表达较多具体的思维,起着解决问题的定性作用,因此我们可以把数的对应——形找出来,利用图形来解决问题。
例3.当n为正整数时,求12+14+18+...+12n的值。
分析:本题对于初中的学生来说还是非常难的,我们可以考虑用数形结合思想来解决。
我们可以这样理解,假设有一个边长为1的正方形,用剪刀去剪这个正方形纸片,第一次剪去正方形纸片的一半,正方形剩余面积是12,第二次剪去剩余图形的一半,得到的图形面积是14,第三次剪去第二次剪剩的图形的一半,得到的图形面积是18,即每次剪去前一次剩余图形面积的一半,……那么当第n次剪后得到的图形面积是(12)n,把每次剪下来的图形面积相加,即得到1-12n=12+14+18+...+12n
通过以上几个例题,我们不难看出,利用数形结合的思想确实很巧妙地化难为易。总而言之,“数无形不直观,形无数难入微”。见到数量就要考虑它的几何意义,见到图形就应考虑它的代数关系,运用数形结合的思想解决数学问题。因此数形结合思想在初中数学教学中起着举足轻重的作用。
其次谈谈如何充分利用空间观念去解决常见数学问题。
空间观念是创新精神所需的基本因素,没有空间观念,几乎谈不上任何发明创造,许多的发明创造都是以实物的形态呈现的,都是设计者先根据想象画出设计图,然后再做出模型,最后才完善成功的。在这过程中空间观念起着非常重要的作用,所以明确空间观念的意义,认识空间观念的特点,发展学生的空间观念非常重要。
例1.已知等边△ABC,以AC为腰,在△ABC外作等腰三角形,AD=AC,连接BD,则∠BDC= °
解析:此题解法比较多,一种解法就是可以根据AB=AC=AD得到A,B,C,D四点共圆,再利用圆周角定理得出∠BDC=30°
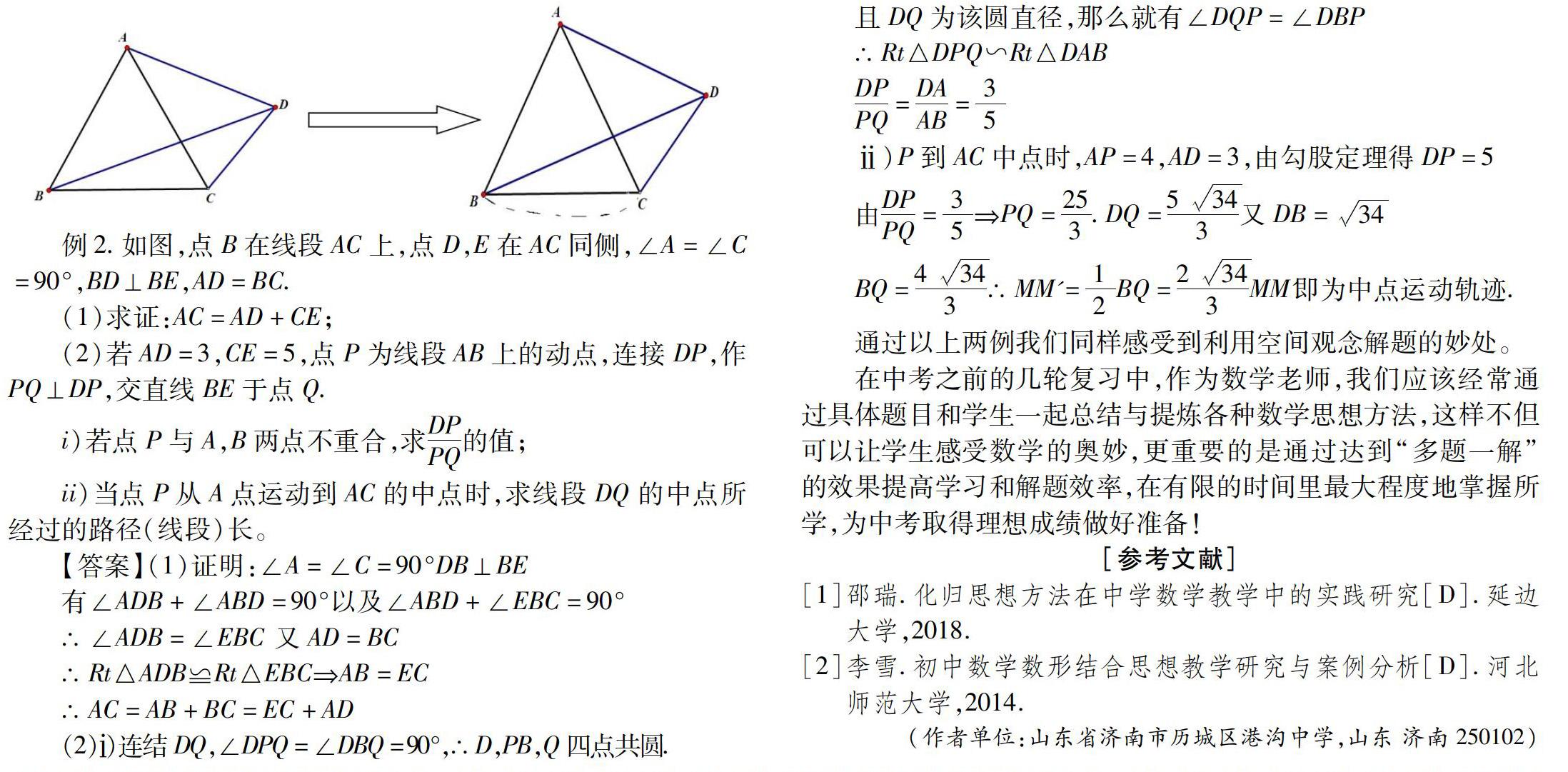
例2.如图,点B在线段AC上,点D,E在AC同侧,∠A=∠C=90°,BD⊥BE,AD=BC.
(1)求证:AC=AD+CE;
(2)若AD=3,CE=5,点P为线段AB上的动点,连接DP,作PQ⊥DP,交直线BE于点Q.
i)若点P与A,B两点不重合,求DPPQ的值;
ii)当点P从A点运动到AC的中点时,求线段DQ的中点所经过的路径(线段)长。
【答案】(1)证明:∠A=∠C=90°DB⊥BE
有∠ADB+∠ABD=90°以及∠ABD+∠EBC=90°
∴∠ADB=∠EBC 又AD=BC
∴Rt△ADB≌Rt△EBCAB=EC
∴AC=AB+BC=EC+AD
(2)ⅰ)连结DQ,∠DPQ=∠DBQ=90°,∴D,PB,Q四点共圆.
且DQ為该圆直径,那么就有∠DQP=∠DBP
∴Rt△DPQ∽Rt△DAB
DPPQ=DAAB=35
ⅱ)P到AC中点时,AP=4,AD=3,由勾股定理得DP=5
由DPPQ=35PQ=253.DQ=5343又DB=34
BQ=4343∴MM'=12BQ=2343MM'即为中点运动轨迹.
通过以上两例我们同样感受到利用空间观念解题的妙处。
在中考之前的几轮复习中,作为数学老师,我们应该经常通过具体题目和学生一起总结与提炼各种数学思想方法,这样不但可以让学生感受数学的奥妙,更重要的是通过达到“多题一解”的效果提高学习和解题效率,在有限的时间里最大程度地掌握所学,为中考取得理想成绩做好准备!
[参考文献]
[1]邵瑞.化归思想方法在中学数学教学中的实践研究[D].延边大学,2018.
[2]李雪.初中数学数形结合思想教学研究与案例分析[D].河北师范大学,2014.
(作者单位:山东省济南市历城区港沟中学,山东 济南 250102)

