3.3一元二次不等式及其解法 教学设计

辽宁省抚顺德才高级中学 季 艺

学习目标：

知识与技能：

理解一元二次不等式解法与二次函数的关系本质，继续探究一元二次不等式解法的步骤和过程；

过程与方法：

培养数形结合的能力，一题多解的能力，培养抽象概括能力和逻辑思维能力；

情感、态度与价值观：

激发学习数学的热情，培养勇于探索的精神，勇于创新精神，同时体会从不同侧面观察同一事物思想。

重点：

从实际情境中抽象出一元二次不等式模型；一元二次不等式的解法.

难点：

理解二次函数、一元二次方程与一元二次不等式解集的关系.

教材分析：

本内容的地位体现在它的基础性，作用体现在它的工具性。一元二次不等式的解法是初中一元一次不等式或一元一次不等式组的延续和深化，对已学过的集合、函数等知识的巩固和运用具有重要作用，同时也为后面线性规划、直线与圆锥曲线以及导数等内容做铺垫。因此，一元二次不等式的解法在整个高中数学教学中具有很强的基础性。

学情分析：

学生在初中已经学习了一元一次不等式（组）和二次函数，对不等式的性质有了初步了解，并在必修一第一章集合中也有学习，学生会习惯转化成不等式组的方法来求解，但不是本节的重点，因此借助函数图象解决不等式问题学生会存在很大问题。

教学准备：

学生预习“一元二次不等式及其解法”第一课时的内容；

教师认真备课，做好相关课件。

教学方法：

探究法、讲授法、启发式教学

教学过程

【新知探究】探究点一 一元二次不等式的概念思考1.考察下面含未知数x的不等式：15x2＋30x－1＞0和3x2＋6x－1≤0这两个不等式有什么共同点？【Q1】答：(1)含有一个未知数x；(2)未知数的最高次数为2.一元二次不等式：(1)一般地，含有一个未知数，且未知数的最高次数是2的整式不等式，叫做一元二次不等式.(2)一元二次不等式的一般表达形式为:ax2＋bx＋c＞0(a≠0)或ax2＋bx＋c＜0(a≠0)，其中a，b，c均为常数.1 mim 1 mim探究点二 “三个二次”之间的关系思考1 对于二次函数与怎样的不等式是等价关系？【Q2】答：f x ax bx c a()(0)= + + ≠2，不等式f x＞()0，或f x＜ a≠()0(0)30s ax bx c a 2+ + ＞ ≠0(0)，或ax bx c a 2+ + ＜ ≠0(0).思考2 作出二次函数f x ax bx c a()(0)= + + ≠2的大致的图象，想一想不等式f x＞()0，或f x＜ a≠()0(0)的解集与30s二次函数有什么关系？【Q3】答：就是分别使二次函数f(x)的函数值为正值或负值时自变量x的取值的集合.思考3 一元二次方程f(x)＝0 (a≠0)的解集与二次函数f(x)有什么关系？【Q4】答：就是使二次函数f(x)为零时自变量x的取值的集合.师总结：一元二次不等式ax2＋bx＋c＞0 (a≠0)，或ax2＋bx＋c＜0 (a≠0)的解集为其对应的二次函数f(x)的函数值为正值或负值时自变量x的取值的集合.f x()15s 30s探究点三 一元二次不等式的解法思考1 二次方程 的零点有怎样的关系？【Q5】答：方程2 6 0 x−x− =的根与二次函数2 6 y=x −x−2 6 0 x−x− =的判别式Δ＝1－4·1·(－6)＝25＞0，可知这个方程有两个不相等的实数根，解此方程得.所以二次方程的根就是二次函数的零点.思考2 画出二次函数x1=−2，x2=3.所以二次函数有两个零点：x1=−2，x2=3 2 6 y=x −x−的图象，你能通过观察图象，获得不等式2 min 3 min 2 6 0 x−x− ＞ 及2 6 0 x−x− ＜ 的解集吗？【Q6】答：二次函数 的图象如图，观察函数图象可知：当2 6 y=x −x−时，函数图象位于x轴上方，此时，y＞0，x＜−2，或x＞3即2 6 0 x−x− ＞ 的解集为{| 2 3}x x＜− 或x＞ ；当时，函数图象位于x轴下方，此时−＜＜2 x 3 y＜0，即−＜＜2 x 3；所以，不等式.【图象法】思考3 由于2 6 0 x−x− ＜ 的解集是{|2 3}x− ＜x＜2 6 (3)(2)x x x x− −= − +，所以解2 6 0 x−x− ＞ 就是解(3)(2)0 x− x+ ＞ ，那么如何解不等式1 min(3)(2)0 x− x+ ＞? 【Q7】 【代数法】

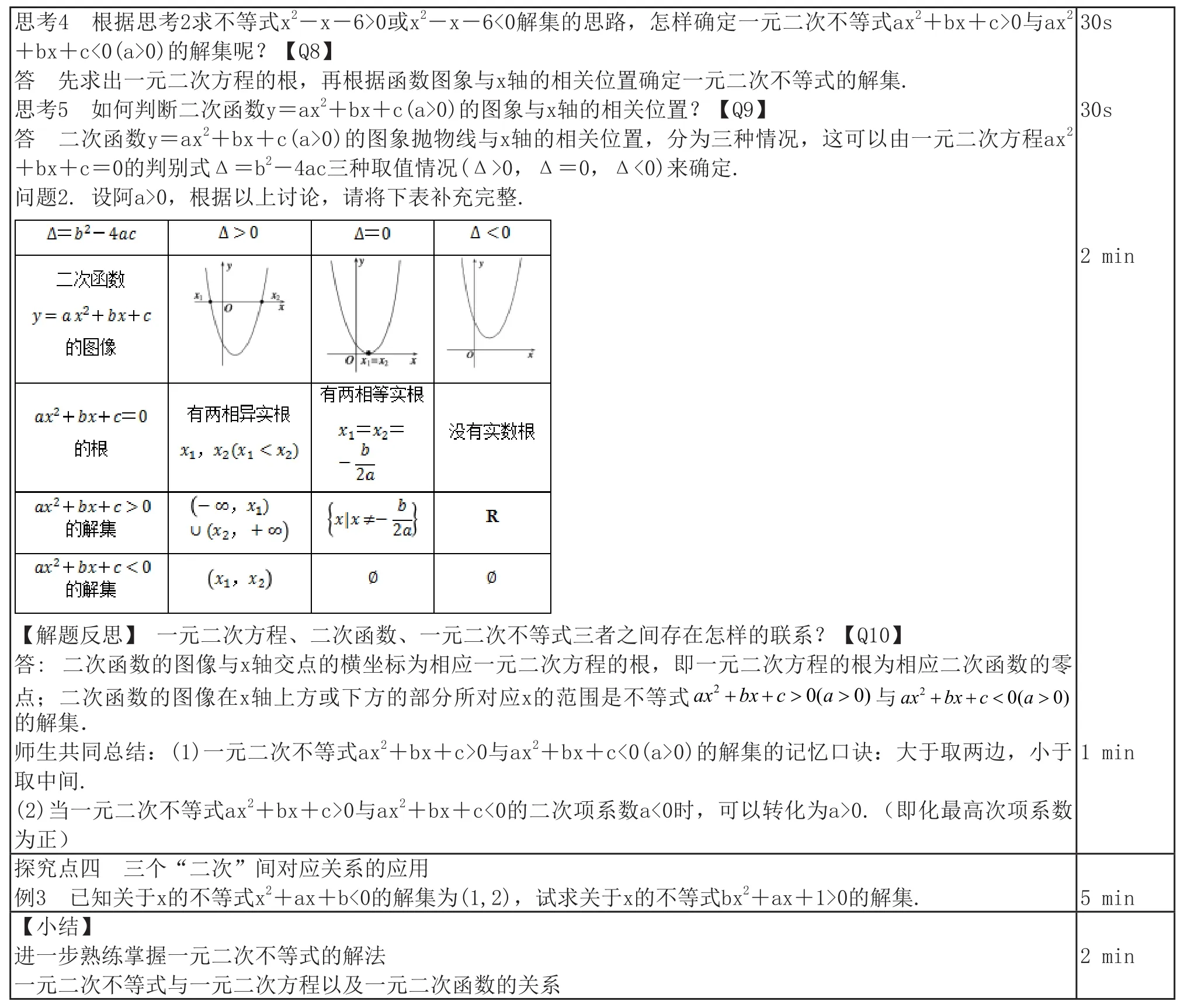
思考4 根据思考2求不等式x2－x－6＞0或x2－x－6＜0解集的思路，怎样确定一元二次不等式ax2＋bx＋c＞0与ax2＋bx＋c＜0(a＞0)的解集呢？【Q8】答 先求出一元二次方程的根，再根据函数图象与x轴的相关位置确定一元二次不等式的解集.思考5 如何判断二次函数y＝ax2＋bx＋c(a＞0)的图象与x轴的相关位置？【Q9】答 二次函数y＝ax2＋bx＋c(a＞0)的图象抛物线与x轴的相关位置，分为三种情况，这可以由一元二次方程ax2＋bx＋c＝0的判别式Δ＝b2－4ac三种取值情况(Δ＞0，Δ＝0，Δ＜0)来确定.问题2.设阿a＞0，根据以上讨论，请将下表补充完整.30s 30s2 min【解题反思】 一元二次方程、二次函数、一元二次不等式三者之间存在怎样的联系？【Q10】答: 二次函数的图像与x轴交点的横坐标为相应一元二次方程的根，即一元二次方程的根为相应二次函数的零点；二次函数的图像在x轴上方或下方的部分所对应x的范围是不等式ax bx c a 2+ + ＞ ＞0(0)与ax bx c a 2+ + ＜ ＞0(0)的解集.师生共同总结：(1)一元二次不等式ax2＋bx＋c＞0与ax2＋bx＋c＜0(a＞0)的解集的记忆口诀：大于取两边，小于取中间.(2)当一元二次不等式ax2＋bx＋c＞0与ax2＋bx＋c＜0的二次项系数a＜0时，可以转化为a＞0.（即化最高次项系数为正）1 min探究点四 三个“二次”间对应关系的应用例3 已知关于x的不等式x2＋ax＋b＜0的解集为(1,2)，试求关于x的不等式bx2＋ax＋1＞0的解集. 5 min【小结】进一步熟练掌握一元二次不等式的解法一元二次不等式与一元二次方程以及一元二次函数的关系2 min