《2.2.2等差数列的前n项和（1）》教学设计

辽宁省抚顺德才高级中学 张 雷

一、教学目标

1.情感态度与价值观

（1）获得发现的成就感，逐步养成科学严谨的学习态度，提高代数推理的能力。

（2）注重在学习过程中师生情感交流，鼓励学生自主发现，激发学生的学习热情，培养学生的探索精神与创新意识。

2.过程与方法

（1）通过公式的探索、发现，在知识发生、发展以及形成过程中培养学生观察、联想、归纳、分析、综合和逻辑推理的能力；

（2）利用以退求进的思维策略，遵循从特殊到一般的认知规律，让学生在实践中通过观察、尝试、分析、类比的方法导出等差数列的求和公式，培养学生类比思维能力。

3.情感态度与价值观

（1）获得发现的成就感，逐步养成科学严谨的学习态度，提高代数推理的能力。

（2）注重在学习过程中师生情感交流，鼓励学生自主发现，激发学生的学习热情，培养学生的探索精神与创新意识。

二、教学重点

等差数列前n项和公式是重点。

三、教学难点

等差数列前n项和公式的推导过程。

四、教材分析

《等差数列的前n项和》是人教实验版必修5第二章第3节的内容，是学生学习了等差数列的定义 、通项公式后，对等差数列知识的进一步学习。

五、学情分析

学生通过对等差数列基本概念和通项公式的学习，，对等差数列有了一定的了解。但是由于学生是第一次接触到数列的求和,缺乏相关经验,因此，需要借助几何直观学习和理解。

六、教具准备

教科书（必修5）及多媒体课件

七、教学方法

利用计算机多媒体辅助教学，采用启发式、探究式、讲练结合教学法相结合。

在教学中通过生动具体的现实问题，激发学生探究的兴趣和欲望，由浅入深，层层深入，增强学生学好数学的心理体验，产生热爱数学的情感,体验在学习中获得成功。

八、教学过程

（一）创设问题情境

故事引入：泰姬陵坐落于印度古都阿格，是十七世纪莫卧儿帝国皇帝沙杰罕为纪念其爱妃所建，她宏伟壮观，纯白大理石砌建而成的主体建筑叫人心醉神迷，成为世界七大奇迹之一。陵寝以宝石镶饰，图案之细致令人叫绝。传说陵寝中有一个三角形图案，以相同大小的圆宝石镶饰而成，共有100层，奢靡之程度，可见一斑。你知道这个图案一共花了多少宝石吗？

问1：高斯早在10岁的时候就已经解决了这个问题，高斯到底用了什么巧妙的方法呢？你能叙述一下吗？

高斯的方法：

首项与末项的和：1+100=101

第2项与倒数第2项的和：2+99=101

第3项与倒数第3项的和：3+98=101

……

第50项与倒数第50项的和：50+51=101

∴前100个正整数的和为：101×50=5050

同学们很容易就把本题用高斯算法解决了。

问2：高斯的思路有什么特点？适合哪种类型？

问3：如果是项数为奇数的数列求和，高斯的办法行吗？能否有更简洁的求法？以下面问题为例，请你解决这个问题？

探究1：第1层到第21层一共有多少颗宝石？

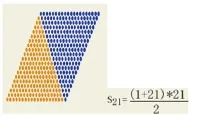
将两个三角形拼成平行四边形.让学生初步形成数形结合的思想,这是在高中数学学习中非常重要的思想方法.借助图形理解逆序相加,也为后面公式的推导打下基础.因此在教学中，要鼓励学生借助几何直观进行思考，揭示研究对象的性质和关系，从而渗透了数形结合的数学思想。

至于人家是否采纳他的菜单，柳知客不管。但在遇事时，他会睁开那对泛黄的像羊眼般的眼睛，伸长那如鹅脖子觅食般的长颈，到各桌检查一番。如果有他菜单上的，便说人家菜的档次高；如果无他菜单上的，便一脸三红地说人家是漂汤菜。同时，他不要主家相邀当知客，还主动义务地行使知客的权力，帮助安排座位。他安排座位有两套方案：一是按年龄大小辈分高低安排；二是一旦遇上当点职务的，不论年龄大小，也不论辈分高低，他的脸上立即堆满笑容，连劝带拽地把人家安排在上席，以致闹出家族中遇事，六十多岁的祖辈人陪三十多岁的侄孙子的笑话。

上述故事归结为 1.这是求等差数列1，2，3，…，100前100项和

2.求等差数列1，2，3，…，21前21项和

（二）等差数列求和公式

1.思考：受高斯的启示，我们这里可以用什么方法去求和呢？思考后知道，也可以用“倒序相加法”进行求和。

我们用两种方法表示Sn：

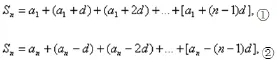
由①+②，得

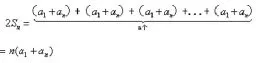
对于这个公式，我们知道：只要知道等差数列首项、尾项和项数就可以求等差数列前n项和了。

问4：由目前的前n项和公式，能否用首相，公差和项数去表示前n项和公式吗？

引导学生思考这两个公式的结构特征得到：第一个公式反映了等差数列的任意的第k项与倒数第k项的和等于首项与末项的和这个内在性质。第二个公式反映了等差数列的前n项和与它的首项、公差之间的关系，这两个公式的共同点都有四个量，都有a1和n，都可以“知三求一”，不同点是第一个公式还需知道an，而第二个公式是要知道d，解题时还需要根据已知条件决定选用哪个公式。

（三）公式运用，变式训练

例1.根据下列各题中的条件，求相应的等差数列｛an｝的Sn：

（1）a1=5，an=95，n=10

（2）a1=100，d=－2，n=50

例2、计算

（1） 5+6+7+…+79+80

问5：这个问题中，首项，末项，项数分别是多少？

（2） 1+3+5+…+（2n-1）

（四）课后小结

2.等差数列前n项和公式的推导方法——倒序相加法；

3.在两个求和公式中,各有五个元素,只要知道其中三个元素,结合通项公式就可求出另两个元素.

（五）课外作业

必修五教材 P41：练习A所有题

九、教后反思

（1）在公式的讲解上一定要注意其特点的讲解，要让学生会区分这两个公式的使用条件；

（2）要告诉学生不一定给首项，末项和项数求和，还可能给和求其他内容，也就是公式的应用是知三求一，不要思维定式了；

（3）最后在计算上注意过程的书写及计算的准确性。