“方程的根与函数的零点”教学设计

天津市静海区运河学校 吴 玥

一、教学目标

1.知识与技能

（1）了解函数零点的概念，理解并掌握方程的根与函数的零点之间的关系；

（2）理解函数零点存在的条件，掌握函数零点存在性的判断，并能求出具体函数零点存在的大致区间.

2.过程与方法

学生经历观察发现、抽象概括、反思构建的过程，体会函数与方程、数形结合及转化化归的数学思想方法，并在过程中探究方程的根与函数的零点的关系，最终能将一个方程求解问题转化为一个寻找函数零点问题并会判断存在零点的区间；

3.情感、态度、价值观

通过对方程的根与函数的零点的探究过程，提高学习数学的兴趣与信心，体验从系统的角度去思考局部问题的思想，培养辩证思维.

二、教学重难点

重点：方程的根与函数的零点的关系、函数零点的存在条件.

难点：准确理解函数零点的存在条件，并针对具体函数（方程）能求出存在零点（根）的区间.

三、教学过程

（一）问题提出

问题1 求解下列方程：

（1）x2−1=0;

（2）x2−3 x + 2 =0;

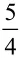
（4）x5+4 x +1 = 0.

设计意图：从学生所熟悉的一元二次方程开始，前三个方程复习了之前学过的解方程的方法.第四个方程为学生创设了一个充满疑难、困惑和障碍的情境，学生产生困惑，从而引发学生思维.

问题2方程（4）有实数根吗？有求根公式吗？

设计意图：在学生已产生困惑的前提下，引导学生将惑转化为外显的问题，从而将本节课探究的重点放在如何找出方程的根，引出课题.

问题3我们怎么判断方程（4）根的情况呢？请大家分组讨论.

设计意图：对学生的惑进一步加强，并引导学生通过讨论发现解决问题的方法.在这一过程中培养学生的合作意识和探究精神.

（二）问题探究

1.方程的根与函数的零点探究

问题1这个猜想可行吗？我们先通过前三个方程来验证一下.请画出前三个方程的对应函数图象.

问题2 你能发现方程的根与对应的函数图象之间有什么样的关系吗？

设计意图：引导学生通过观察方程的根与函数的图象，得出猜想，培养学生的观察能力和抽象概括能力.

问题3我们刚刚对三个特殊的一元二次方程得出的猜想对一般的一元二次方程ax2+bx+c=0(a≠0)还成立吗？

教师利用几何画板画出一般的一元二次方程ax2+bx+c=0(a≠0)所对应的函数图象，并对a,b,c任意取值.引导学生观察方程的根和其对应的函数图象之间的关系，验证猜想.

设计意图：在问题2的基础上将问题一般化，并引导学生通过观察验证猜想，得出结论.学生经历了先猜后证的过程并从中体会由具体到抽象、由特殊到一般的过程，体会数形结合的数学思想方法，培养观察能力.

问题4对于一个有两个根x1, x2的一元二次方程，我们把x1, x2叫做这个方程的根；对于函数图象，把x1, x2叫做函数图象与x轴交点的横坐标.对于函数来说，我们把x1, x2叫什么呢？

设计意图：从不同角度对x1, x2加以解释，并引导学生产生新的惑，引发学生积极思维，并从函数的角度对x1, x2加以解释和命名，进而引出函数零点的概念.

问题5对于一个一般的二次函数，在Δ ＞ 0 ,Δ = 0 ,Δ ＜0三种情况下，它的零点分别是什么？

设计意图：巩固函数的零点的概念.

2.函数零点的存在条件的探究过程

问题1是不是所有函数都存在零点呢？你能画出一些不存在零点的函数图象吗？

设计意图：在学生已经了解了函数零点的概念的基础上，促使学生思考是否所有函数都存在零点，产生新的疑惑，并鼓励学生举出反例，培养学生的辩证思维能力.

问题2 观察图象，你能发现在什么情况下函数是存在零点的？

表2

设计意图：学生通过观察函数图象，初步发现函数零点存在的条件.同时，在这一过程中培养学生的观察能力.

问题3如果一个函数y=f(x)的图象在区间[a, b]内穿过x轴，就说这个函数存在零点，那你能用数学语言来描述吗？

教师引导学生观察零点左右两侧的函数值的特点，得出f(a)·f(b)＜ 0.

设计意图：引导学生将自然语言转化为符号语言，将对几何图形的描述转化为数学式子，培养学生数形结合思想和抽象概括能力.

问题4在一个区间[a, b]上，如果函数y=f(x)有f(a)·f(b)＜ 0，那么这个函数一定存在零点吗？你能举出反例吗？

学生思考后画出符合条件但不存在零点的函数图象（如图2、图3）.

设计意图：通过这一问题再次引发学生的惑，并鼓励学生思考、举出反例，培养学生的辩证思维能力.

问题5那函数y=f(x)在区间(a,b)上存在零点，除了f(a)·f(b)＜ 0外，还需要什么条件呢？

设计意图：学生通过观察，发现函数图象是连续不断的这一条件，达到解惑的目的，培养学生的观察与概括能力.

函数零点的存在条件：略.

（三）新知应用

例1求函数f(x)=lnx+2x−6的零点的个数.

设计意图：在经历了不断地生惑、解惑的过程后，学生已基本掌握了新知识.通过例题对新知识进行巩固，通过思路分析，引导学生进一步思考与理解新知，掌握解决问题的思路与方法，培养学生能力，达到增识的目的.

（四）课堂小结

问题1本节课中利用到了哪些知识与数学的思想方法？

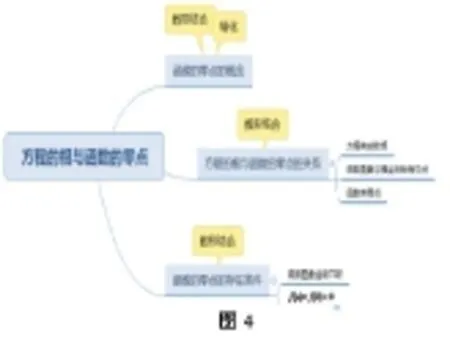
设计意图：引导学生从数学知识和数学思想方法两个角度对本节课的内容进行总结，形成思维导图（如图4）.