结语留有余地 拓宽思维广度

宁夏固原市泾源县兴盛乡红旗小学 李广得

在日常生活之中说话做事都应当留有余地，以免绝对而没有回旋的余地。数学教育教学活动中，教师说话，尤其是一些教学结语的总结表达更不能绝对化，而应当留有余地，讲究科学性和准确性，做到瞻前顾后，有拓展性。这些年的教学感触颇深，下面以实例为证。

在教学三角形的面积公式：三角形面积 = 底高÷2时，相当一部分教师一次又一次的强调或者告诫学生注意：“要求三角形的面积必须知道三角形的底和高”。这样强调“必须”是否恰当？是否科学？

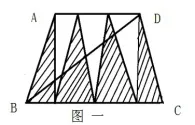
我们都知道，即使在小学阶段要求三角形的面积，也未必一定要知道这个三角形的底和高，我们可以通过其他方法或途径来计算，我们不能一味的强调，给学生的思维加上圈套形成一种定势，遇到问题死钻牛角尖，而失去灵活的思维。如下题,右图一所示：已知梯形ABCD 的面积是50平方厘米，三角形ABC 的面积是20平方厘米，求图中阴影部分的面积？学生感觉到困难重重，束手无策。根源何在？就是由于我们在教学中的数学语言表达太过绝对，“要求三角形的面 积必须知道三角形的底和高”这一死板的表述，束缚学生的思维，导致本题无法求出阴影部分的面积。其实本题不必知道三角形的底和高就能求出阴影部分的面积，我们可以引导学生从等底等高的三角形的面积相等入手，帮助学生理解空白处的图形，其实就是和三角形ABC是一个等底等高的三角形，进而使学生明白用梯形的面积减去三角形ABC的面积就得到阴影部分的面积。即阴影部分的面积=50-20=30平方厘米。

随着学习进一步深化，到中学以后就可以发现，求三角形的面积公式有十几个之多。而我们小学教师说：“要求三角形的面积必须知道三角形的底和高”显然是不科学的。

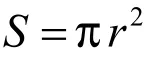
同样在圆面积公式的应用当中,也有教师特别强调：“要求圆的面积必须知道圆的半径”。我也曾犯了同样的错误，表述太绝对，没有留余地。例如右图二所示：已知正方形的面积等于52平方厘米，圆的直径是2r,求阴影部分的面积。如果学生至从求出半径,再求出圆的面积这条

路去思考,就会钻入死角，以失败而告终。其实解题途径之一，就是可以通过正方形面积=2r×2r =52平方厘米，得出 r2=13平方厘米,进而求出圆的面积，再求出阴影部分的面积。即：圆的面积=3.14×13=40.82平方厘米，阴影部分的面积=52-40.82 = 11.18 平方厘米。

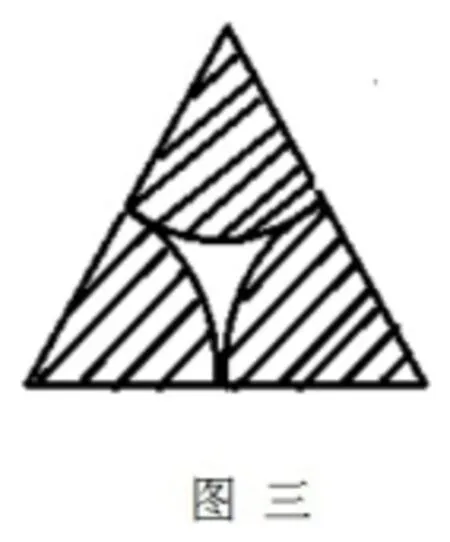
正在上小学六年级的儿子拿来一道求阴影部分面积的题,让我给他讲，如右图三所示：已知扇形的半径为5厘米，求阴影部分的面积是多少平方厘米？初看此题我还有些懵，平常所见求阴影部分的面积的题型大多数都是用大图形的面积减去小图形的面积，而这道题有点“怪”。儿子这时似乎看出了一些门道:“这是一个等边三角形，它的每一个角都是60°”。和儿子商讨之际我一下子脑洞大开，说出了计算过程：三角形内角和是180度，只要求出圆的面积，再算出它的一半。很可惜的是我一下打断了儿子的思维，这或许就是我们这些当老师的一个通病：没能留给学生更多的时间思考和再次表达的机会，为学生的思维发展搭建更好的平台。这道题可以利用圆的半径计算出圆的面积,因为此题中三角形是等边三角形，三个内角的和是180°，所以阴影部分拼起来的面积就是圆面积的一半。即：阴影部分的面积=3.14÷2=24.25平方厘米。紧接着我又引导儿子归纳出：普通三角形三个角上都画有半径相同的扇形,它的面积也可以用求出三角形内角和的办法，求出圆的面积的一半去计算。

总之，教师把一些结语讲的过分“绝对”，学生则学的“呆板”，解题时思维受阻,思路狭窄，直接影响学生思维能力的培养和提高。因此，我们在备课、做课过程中的教学用语必须仔细推敲和斟酌，留给学生更多的空间，发挥学生的思维想象能力，说话要留有余地，才能更好的拓宽学生的思维。