具有尖峰解的三分支 Camassa-Holm 系统的一种弱解的局部弱适定性∗
张媛媛,胡巧怡
(华南农业大学数学与信息学院,广东 广州 510642)
本文研究以下Camassa-Holm (CH)系统的Cauchy问题:
(1)
其中,m=u-uxx,n=v-vxx,l=w-wxx。定义:
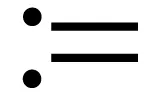
(2)
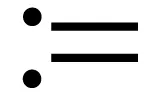
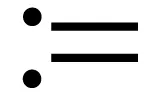
(3)
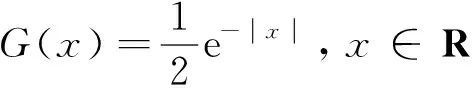
(4)
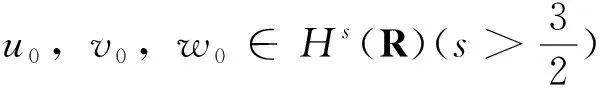
mt+2mux+umx=0(m=u-uxx,x∈R,t∈R+)
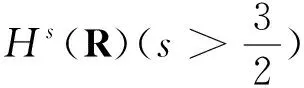
当w≡0时,问题(1)成为了一个双分支CH方程[19]
1 积分系统的形式推导
取α=u+v+w的流φ:R→R,即
(5)
假设方程(5)有唯一解,对其两边关于s求导,可解得φs(s,t)>0,(s,t)∈R×R+。令
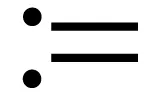
(6)
现构造拉格朗日坐标系下的新向量场(Γ,M,N):
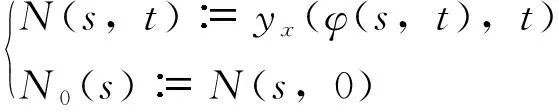
(7)
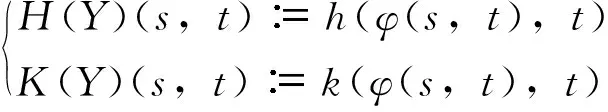
(8)
根据式(4)-(8),以及G′′*f=G*f-f(f∈L2),可得
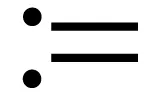
(9)
[-G*(H(Y)∘ψ)-G′*(K(Y)∘ψ)]·
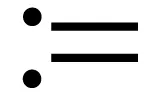
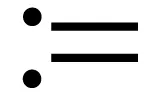
(10)
[-G′*(H(Y)∘ψ)-G*(K(Y)∘ψ)+
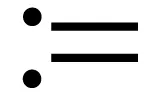
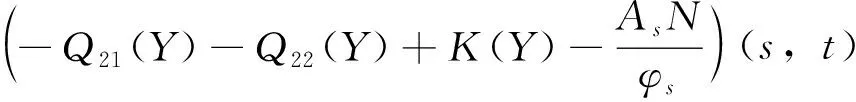
F3(Y)(s,t)
(11)
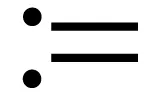

(12)
另外,再次利用G′′*f=G*f-f(f∈L2),易得以下结论
∂sQ11(Y)=φS·Q21(Y),∂sQ12(Y)=
φS·[Q22(Y)-K(Y)],
∂sQ21(Y)=φS·[Q11(Y)-H(Y)],
∂sQ22(Y)=φS·Q12(Y)
(13)
此结论将在后文中被多次运用。
2 预备引理
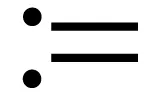
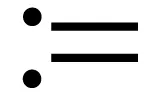
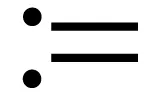
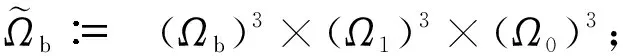

由上述定义易知,对∀φi-Id∈H1∩W1,∞(i=1,2),φi∉L2∪L∞(i=1,2), 但φ1-φ2∈H1∪W1,∞。另外,由于ψx(x,t)=φs(ψ(x,t),t)-1,故
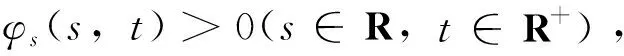
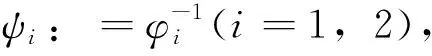
证明以下省去t。因为φi∘ψi=Id(i=1,2),故
(ψ1-ψ2)(x)=
ψ2∘φ2(ψ1(x))-ψ2∘φ1(ψ1(x))≤
b-1φ2(ψ1(x))-φ1(ψ1(x))
证毕。
引理2 若φ∈C1(R+;L∞),则ψt=-ψxφt∈L∞。
证明任取t0∈R+,对∀(x,t)∈R×R+,利用φ∘ψ=Id,可得
-ψx(φ(s,t0),t)φt(s,t0)
证毕。
3 积分系统解的存在唯一性
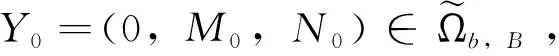
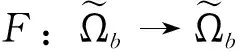
和
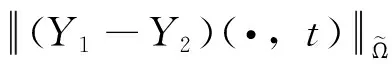
(i,j=1,2)
由式(8)中H,K的定义、引理1,易得
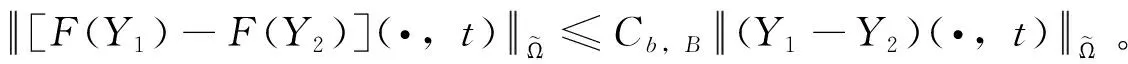
4 系统等价
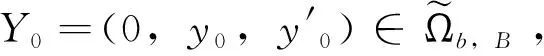
yx(x,t)=N(ψ(x,t),t)
(14)
Mst=(-Q11-Q12+K)(Y)·φs,φst=As,
于是Jt≡0,又因为J0=0,故J≡0。矛盾,式(14)得证。
下面证明以上构造的解y∈X。由(y,yx)=(M∘ψ,N∘ψ)易得y(·,t)∈(H1∩W1,∞)3。
又因为
(t1,t2∈(0,T])
对右边第一项做如下放缩,
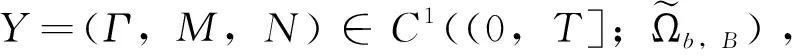
y∈C((0,T];(H1∩W1,∞)3)
根据系统(4),显然有yt(·,t)∈(L2)3。利用系统(4)及Young不等式,有
借助h和k的定义,易得它们关于时间的连续性,又因为y∈C((0,T];(H1∩L∞)3),所以
y∈C1((0,T];(L2)3)
现在开始本命题第二部分的证明。由于y∈L∞((0,T];(W1,∞)3),故α(·,t)=(u+v+w)(·,t)是R上的利普希兹连续函数,从而

(15)
在C1((0,T];W1,∞)上有唯一解,且解为一微分同胚。类似式(6)-(8)构造A、Γ、M、N、Y、H和K,下面证Y满足方程(12)。类似式(9) -(10)的推导,易得
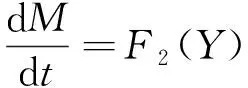
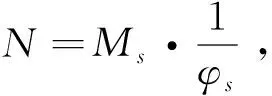
则
由式(13)可得
Mst=∂sF2(Y)=∂s(-Q11-Q12)(Y)=
φs(-Q21-Q22+K)(Y)=φsF3(Y)+As·N
于是
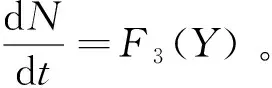
证毕。
由命题1知,系统(12)有局部唯一解,故由命题2中系统(4)的Cauchy问题与系统(12)的等价性可推得,系统(4)有局部唯一解。
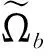
命题3 任给y0i∈(H1∩W1,∞)3(i=1,2), 存在Ti(i=1,2),使得
yi∈C1((0,Ti];(L2)3)∩C((0,Ti];
(H1∩L∞)3)∩L∞((0,Ti];(W1,∞)3)(i=1,2)
满足方程(4),且
其中T=min{T1,T2}。

