基于BMO算法的梁冲击荷载识别∗

谭栋，汪利，吕中荣

(中山大学航空航天学院力学系，广东 广州510275)

结构损伤检测是保证结构安全运营的重要手段。随着现代计算机技术的发展，结构损伤动力检测技术也迅速发展起来。利用采集的振动信息对发生在结构上的损伤进行识别，在航空航天、机械工程等领域都有深入和广泛地应用[1]。而，结构外载的识别是健康监测中重要的一环[2]。例如：一个异常大的冲击荷载作用在结构上易导致结构发生损坏，故对于结构所受的外力进行实时检测具有重要意义。

荷载的识别一般分为两大种类。一方面是直接利用传感器定位荷载的位置，并对其进行重构。Chio和Chang[3]用传感器分布于结构上定位荷载并确定了其大小；Gaul和Hurlebaus[4]运用小波对板上的冲击荷载位置进行了识别，之后压电式传感器也被应用于荷载识别[5-7]。另一方面，越来越多的理论方法被用于荷载参数识别中。Zhu和Law用模态叠加与参数修正对多跨连续桥上的移动荷载进行了识别[8]；Gunawan等采用二次样条插值逼近的方法估测了冲击荷载[9]；Lu和Law采用基于加速度响应的灵敏度方法对结构的外激励进行了识别[10]。一些智能算法，如遗传算法、神经网络算法等，被用于解决各种复杂的优化问题[11-14]。通过结构响应建立目标函数，参数识别问题可以转化为一个优化问题。BMO(bird mating optimizer)由Askarzadeh[15-17]提出，是一种模拟鸟类繁殖特性的新兴群智能算法，具有设置简单、计算精度高的特点。

本文将作用在梁结构上的冲击荷载简化为三角冲击荷载，通过有限元建模得到其动态响应。引入合理的目标函数并结合BMO算法，对冲击荷载的位置、大小和作用时间等参数进行识别。考虑荷载识别中只有动态响应能发挥作用，而加速度响应具有易于测量、信息量大和噪声污染少等特点，在本文中将被采用来进行损伤识别。数值算例表明，在无噪声和有噪声的情况下，冲击荷载的几个参数均能精确识别。

1 基本理论

1.1 简支梁中冲击荷载模型

如图1所示的简支梁，长为L，宽为b，厚度为h，设笛卡尔坐标系分别顺序沿着xyz三个方向。其中，E与ρ分别为梁材料的杨氏模量与密度。

在本文的理论分析中，将对冲击荷载进行参数化从而展开识别。冲击荷载有峰值极高、作用时间极短的特点。设冲击荷载的峰值为Fmax，对于峰值前后荷载为零时的两端时间，可以定义为冲击荷载的加载时间与卸载时间。一般来说，冲击荷载可以设为线性加载、三角函数加载和不规则加载三种模式，假设冲击荷载为最常用的线性三角形冲击荷载。如图1-2所示，设冲击荷载为沿Oz轴方向的F(t)，冲击荷载模型化为四个基本参数：荷载作用点距梁左侧原点的距离为xF，冲击荷载达到最大值时的加载时间tl，经过最大值后荷载的卸载时间tu以及冲击荷载的最大值Fmax。

图1 简支梁模型Fig.1 Model of simply supported beam

图2 三角冲击荷载及其参数Fig.2 Basic parameters of triangular impact

1.2 梁的振动

要量化梁的各项响应，将对梁进行有限元离散。离散时梁单元采用Euler-Bernoulli梁单元进行离散，其中每个单元含有两个节点。通过积分可得到梁的刚度矩阵K与质量矩阵M。当外力F(t)作用在结构上时，其受迫振动方程可由式表示：

(1)

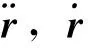
1.3 作用在任意位置的荷载

在本文中，所识别荷载的位置可以是在整个梁上的任意位置。经过有限元划分后，将荷载作用点取为结点，按结构的节点载荷处理，即把单元上的荷载转化为作用于节点的等价节点力。设作用于实际位置的荷载为f(x,t)，则转化后的等效节点力为：

(2)

其中，le表示单元长度，[N]为所采用有限元单元的形函数矩阵。根据本文所用的Euler-Bernoulli梁单元，作用于梁单元上的荷载将被转化为作用于对应单元的节点上的力和弯矩。

1.4 目标函数

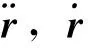
(3)

(4)

其中，n为测点个数。

通过观察式(4)，如果荷载参数向量a与给定的特定冲击荷载参数完全适应的话，那么目标函数就可以取得最小值0，也就是当计算中取到目标函数的最小值时，相应的参数向量就可以表述该次计算中识别的冲击荷载的性质。

2 参数识别方法

2.1 BMO算法

鸟群繁衍优化算法(bird mating optimizer)是由Askarzadeh提出的一种模拟鸟群繁衍模式的进化算法[15]。在BMO算法中，以小鸟来代表一个个体，每个个体都是一个可行解。与自然中的鸟类一样，BMO算法中把小鸟分为雄性和雌性两大类，其中雌性所代表的是所有个体中较优的一部分，一般仅占全部个体的10%。计算中共有五种繁殖方式，雌性小鸟参与三类繁殖：一夫一妻，孤雌生殖和一妻多夫，据此雌性将被分别优和次两组。雄性小鸟也参与三类：一夫一妻，一夫多妻和杂交，而雄性会分为优中差三组。根据不同小鸟的繁衍方式，依照适应度对鸟群进行分类，各类小鸟将按照特定的繁衍方式繁殖后代，这些繁衍方式可用特定的数学公式表达。

(1)一夫一妻

ifr1>mcf

xb(c)=l(c)-r2×(l(c)-u(c))

end

(5)

(2)一夫多妻

较次的雌性个体与优和中两组雄性参与一夫多妻繁衍，对雄性小鸟来说，要通过与多个雌性进行交配，才能产生一个新的后代，这些雌性也通过轮盘赌机制选择。其数学表达如下：

ifr1>mcf

xb(c)=l(c)-r2×(l(c)-u(c))

end

(6)

(3)孤雌生殖

只有基因最好的雌性个体才进行孤雌生殖。繁衍过程可以用数学方法表达为：

fori=1∶n

ifr1>mcfp

xb(i)=x(i)+μ×(r2-r3)×x(i)

else

xb(i)=x(i)

end

end

(7)

其中，mcfp为孤雌生殖中的突变控制指标，r2和r3为[0,1]间的随机数，μ为突变过程中的突变程度控制因子。

(4)杂交

在BMO算法中，采用杂交方式进行繁衍的个体为鸟群中基因最差的个体，均为雄性个体。这里，首先采用混沌序列对这些个体进行变异处理。经过处理后得到的新个体，将遵循式(5)的方式来产生下一代。

(5)一妻多夫

与一夫多妻制相似，一妻多夫制中，基因较差的雌性小鸟通过轮盘赌制选出多个雄性交配对象，交配方式与式(6)中相同。

可以看出，BMO算法中五类繁殖方式均有普通繁殖与变异产生。其中普通繁殖的计算上类似于传统的粒子群算法(PSO)，但在具体分类中更为细致。根据具体的公式与推荐的繁殖方式数量比50∶30∶5∶10∶5[15]，孤雌生殖与一夫一妻制将极大地促进局部搜索，提高识别精度，而几乎每个个体都参与到繁殖中。尽管一妻多夫与杂交中个体质量较差，在杂交中最差的雄性个体将直接被通过混沌序列产生的新个体替换，这将扩大全局搜索能力。同时，每种繁殖方式中都引入了变异，这与遗传算法(GA)的理念相似，但BMO中的变异仅根据mcf决定变异概率，在这之后的变异个体选择上更为随机。而专注于局部搜索的孤雌生殖也采用时变的mcfp来决定变异概率，一般是随更新代数的增加而概率减小；同样的，个体变异权重w一般也随着进化而逐渐减少，这都让最后的个体收敛更为精确。总的来说，BMO结合了之前多种元启发式算法的优点，但仍保证了较高的计算效率，是一种优秀的群智能算法。

2.2 冲击荷载参数识别

综上所述，将有限元梁理论与BMO算法结合，整个参数识别的流程如图3所示，可分为如下几个步骤：

(1)初始化

以所需识别参数向量作为个体，在每个参数对应的搜索空间内，随机生成多个参数向量。

(2)适应度值

把各个体代入目标函数，以目标函数值作为个体的适应度值，来衡量个体的质量。

(3)分类

对所有个体进行分类。首先，将适应度较高的个体归类为雌性，其余的归为雄性。然后在雌性个体中，把适应度最高的个体看作孤雌繁殖的个体，其余雌性个体以一妻多夫制进行繁衍。对于雄性个体，质量最差的一部分将被抛弃，剩余的雄性个体再分为两类，质量较好的将以一夫一妻制进行繁殖，其余的以一夫多妻制进行繁殖。对于被淘汰的个体，用混沌序列产生新的个体，进行杂交。

(4) 繁殖

各类型的个体按照自己的繁衍方式进行繁殖。

(5)优胜劣汰

混合新生个体与原个体，根据适应度评估新生代识别参数的质量，保留更好的个体组成新的种群。

(6)循环

重复步骤(3)-(5)，直到所得的最优个体达到了预设精度要求，或者循环迭代次数达到预设值。

(7)结果

把由BMO 算法得到的最终的最优个体作为该冲击荷载参数的识别结果。

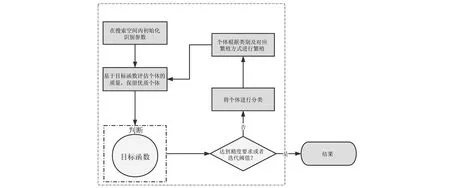
图3 冲击荷载参数识别流程图Fig.3 Flow chart of identification process

3 数值算例

计算中，BMO算法的基本参数设置为：种群数量一共100个，一夫一妻、一夫多妻、杂交、一妻多夫和自交的个体数量分别为50、30、10、5和5。每个一夫多妻和一妻多夫的鸟个体都有3个感兴趣的对象。其他参数的设置为mcf=0.9，μ=0.009，mcfp由0.15至0.8呈线性变化，时间权值因子w由1.9至0.1根据进化步数呈线性变化。在本算例中将不设置精度阈值，最大进化步数设为200步。

3.1 无噪声情况下的参数识别

如图1所示，本算例的简支梁长、宽、高分别为20 m、0.4 m、1 m，材料为钢，材料的杨氏模量E=210 GPa，密度ρ=7 800 kg/m3。利用有限元将梁离散化为12个欧拉伯努利梁单元。在利用目标函数评估个体质量时，取不受噪声影响下的数据。结果将基于两个算例，分别展示作用于节点上和单元内的冲击荷载的识别结果。设两冲击荷载分别为f1及f2。其中,f1作用于第6节点，位于全梁5/12处，加载时间t1l=0.03 s，卸载时间t1u=0.05 s，最大冲击值f1max=3.5×105N，即：

(8)

(9)

其中,f2的等效节点荷载全部根据式(2)计算。算例中计算动态响应时，采用Newmark直接积分法，整个时间历程为1 s，时间步长取0.001 s，基于Rayleigh阻尼模型构建的阻尼系数均取0.01，加速度数据选用节点2、4、6、8、10的加速度数据。各参数的搜索范围见表1。

表1 参数搜索范围Table 1 The searching space of each parameter

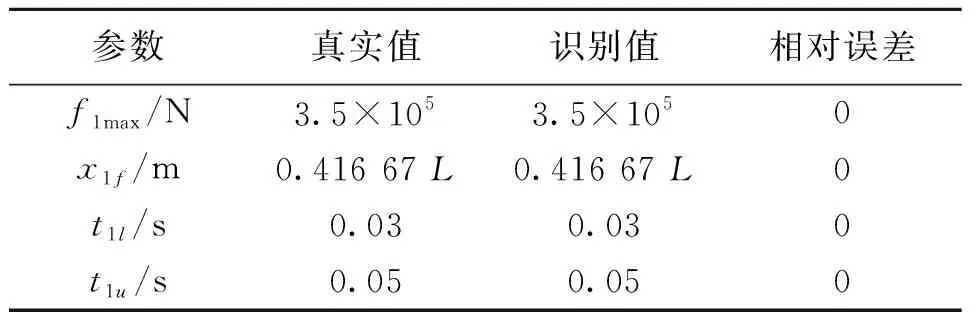
计算5次并取其平均值，得到了表2-3所示的识别结果。结果显示: 计算结果十分稳定，5次识别均与真实值完全吻合。

对f1中某一次识别结果的参数进化情况进行观察，为比较方便，取fmax与xf的识别值除以对应搜索范围的最大值所得数、tl及tu的原值，得到四组介于[0,1]间的值，如图4所示。在图4中，可以看到大约到20步时各参数趋近收敛。而图5中显示的是目标函数的常用对数值的进化曲线，此图中适度值在20步后仍继续减小，至50余步才接近完全收敛，说明之后的进化步数确保了更高的精确度。

图4 各参数的进化曲线Fig.4 Evolutional curves of identified parameters

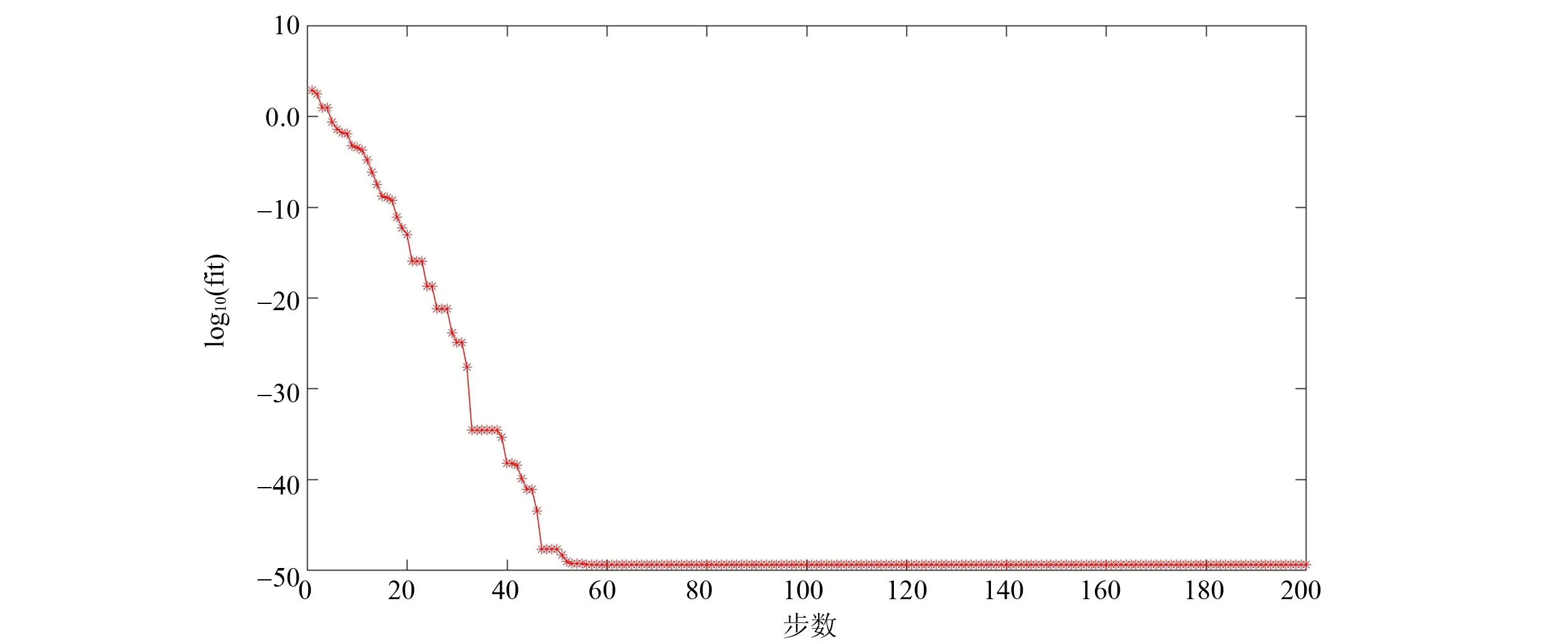
图5 适应度值进化曲线Fig.5 Evolutional curve of fitness value

参数真实值识别值相对误差f1max /N3.5×1053.5×1050x1f/m0.416 67 L0.416 67 L0t1l/s0.030.030t1u/s0.050.050

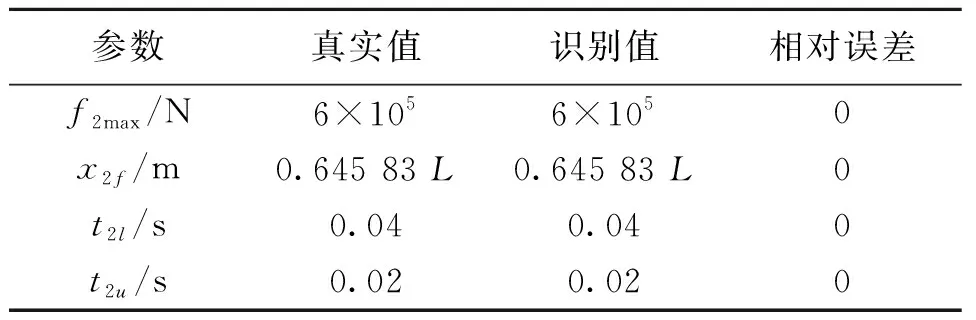
表3 f2识别结果Table 3 The identified results of f2

3.2 噪声情况下的参数识别

为了更好地模拟实际工况，现在基于相同的结构与冲击荷载，讨论响应被噪声污染的情况。假设加速度响应分别被5%和10%的随机噪声污染，随机噪声的模拟形式如下式：

(10)

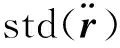
在噪声情况下仍进行5次识别取平均值，并计算方差。f1、f2的识别结果见表4-5。可以发现，在两种噪声水平下，该方法均可以正确识别出参数，且识别结果的相对误差非常小；两个算例中，fmax与xf在5%噪声下，相对误差小于0.1%，而在10%噪声下小于1%；ti与tf识别结果与真实值基本完全吻合；各数据五组值的方差均很小。这说明识别受噪声水平上升的影响很小。

3.3 与其他启发式算法的比较

本文的参数识别涉及四个参数，不算含有大量未知量的问题。但识别所用的加速度采样时间点多数据量大，故每个参数对微小变化的反应较为灵敏；良好地识别该问题需要兼顾局部和全局两组搜索能力。为进一步验证BMO算法的有效性，将之与遗传算法(GA)和粒子群算法(PSO)的识别结果进行对比。其中，遗传算法的基本参数设置为代沟(generation gap)=0.7；粒子群算法中惯性权重w由0.9时变为0.4，局部及全局学习因子c1、c2均为1，速度极限为1。将f2计算5次并取平均值作为识别值，并计算相对误差与方差，得到了表6-7所示的结果。

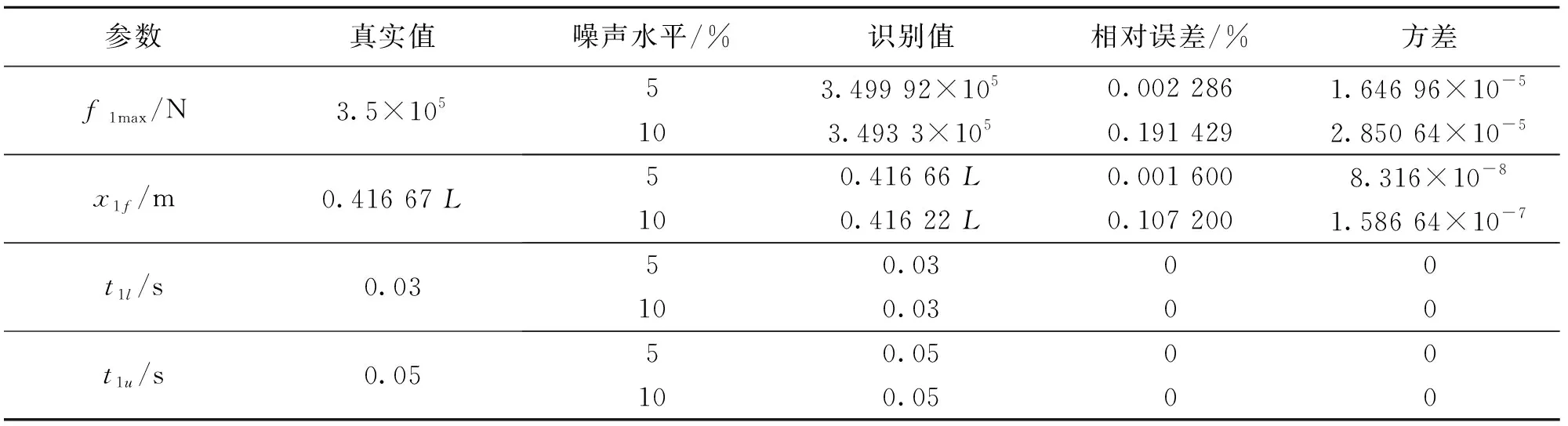
表4 f1识别结果Table 4 The identified results of f1 in noise condition

表5 f2识别结果Table 5 The identified results of f2 in noise condition

表6 遗传算法(GA)识别f2结果Table 6 The identified results of f2by Genetic Algorithm

表7 粒子群算法(PSO)识别f2结果Table 7 The identified results of f2by Particle Swarm Optimization

从表6-7可以看出，由于采取平均值作为识别值，故结果与实际偏离较大。实际计算中，两种算法的识别结果均收敛于[6, 0.66, 0.4, 0.22]与[0.998, 0.372, 0.19, 0.64]两组值。显然，第一组接近真实值，为正确搜索结果；第二组与真实值偏差大，显然是算法陷入了局部最优。可以观察到，在噪声高的情况下，平均识别结果甚至还更好，显然是噪声的存在反而使得第二组数据出现概率更低，识别平均值更佳，这说明两种算法全局搜索能力普遍不如BMO。而粒子群由于寻优计算机制单一，相比拥有变异机制的遗传算法更差，其粒子个体的速度在搜索后期基本趋近于零。算法设定的粒子速度范围选择上约束性也很强。因为其粒子在前期维数更新中极其活跃，过快的速度会使识别值趋向于参数取值范围两侧的局部最优点，过慢的速度会使粒子快速趋于静止，这两种现象还会因前几代个体的具体值在局部最优值附近而加重，使得在初期搜索中即收敛，形成“早熟”现象。为进一步比较算法的局部搜索能力，选择GA与PSO中无噪声情况下的一组正确识别数据，并与BMO的一组识别值进行精度上的对比，结果见表8。

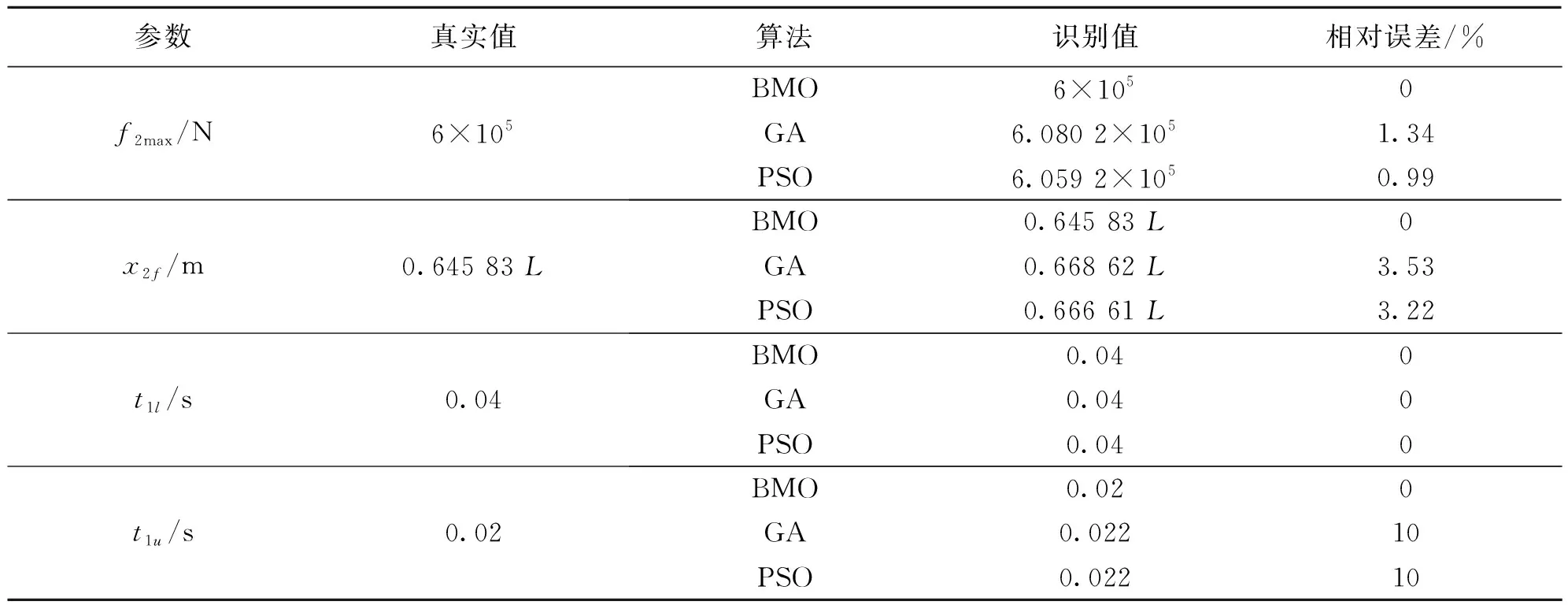
表8 无噪声下多种算法识别f2结果Table 8 An identified result of f2by multiple algorithms in noise free condition

从表8可以看出，BMO算法识别无误差，精确度远高于GA与PSO算法。对应的适应度进化曲线如图6所示。可以看到，BMO算法在初始阶段即快速收敛，而在30代左右GA和PSO算法已经收敛，甚至收敛到了比BMO算法更低的适度值；但之后两者的适应度不再发生变化，而BMO算法在130代左右时再次进一步收敛，得到了非常精确的识别值，最终适应度收敛至10-22的数量级。由此可以看出，BMO算法在进化代数后期有更强的局部搜索能力。

图6 多个算法的适应度进化曲线Fig.6 Evolutional curve of fitness by multiple algorithms

4 结 论

本文将冲击荷载转化为双线性模型并参数化，利用加速度构造目标函数；采用有限元方法进行响应计算，运用BMO算法对作用于梁上的三角冲击荷载参数进行了识别。BMO算法能精确地识别冲击荷载作用的位置、大小和时间等四个参数，计算精度优于遗传算法与粒子群算法。且，BMO算法的优点在于分类别搜索，即不同的繁殖模式，确保了局部搜索的收敛准确，同时较高的变异概率和均等的个体参与产生下一代的权利，使得即便在搜索后期仍能兼顾全局搜索能力，在此类参数识别问题中得到了非常良好的结果。多种噪声情况下，BMO算法依然稳定的识别结果，体现了其有效性和鲁棒性。因此，BMO算法在工程实践中具有一定的应用价值。