电动汽车后轮轮毂电机驱动的操纵控制∗

祁新梅，郑寿森，付青

(中山大学物理学院，广东 广州 510275)

电动汽车以车载电源代替石油能源，以电动机代替内燃机，具有能量转换高、零排放等优点，是目前应对石化能源衰竭和环境恶化问题的首选城市交通工具。现有成熟的电动汽车结构都是基于传统的内燃机汽车的集中驱动机构，除了动力源从内燃机变成电源外，主要动力传递结构与传统汽车类似，由减速器、机械差速和随动系统等把电机输出的力矩传递到车轮上，动力系统体积大、重量大、传动效率低。分布式驱动电动汽车是动力控制的新形式，主要有轮边电机驱动与轮毂电机驱动[1-3]。其中，轮毂电机驱动是将驱动电机直接安装在车轮中，传动效率高、不占用车身空间。另外，适应强振动、多泥水等复杂工况的新型轮毂电机也得到了快速的发展[4-6]。轮毂电机驱动对每个轮独立控制，实现转向、加速、启动、刹车、减速，去掉了底盘中的机械差速系统，缩短了传动链，减轻了汽车重量，简化了汽车结构，提高了可靠性和汽车续驶里程，具有动力系统体积小、传送效率高、可控性强的优点。一但技术成熟并投入实用，是对电动汽车结构的革新。

分布式驱动控制极大地依赖于软硬件的响应速度和控制策略，目前的计算机软硬件能力尤其是嵌入式系统的快速发展，为中速轻型城市交通汽车的分布式实时操控提供了技术上和器件上的支撑，基于轮毂电机分布式驱动的电动汽车逐渐呈现出诱人的应用潜力，轮毂电机协调控制成为研究热点之一。分布式轮毂控制中的控制变量主要是驱动电机的输出转速和转矩[7]，Ackermann模型是转速控制转向的运动学模型，忽略了车辆的横摆运动、计算简单[8]。文献[9]将神经网络用于转速控制，考虑了非线性因素，适用于学习样本所描述的工况。文献[10]根据横摆角速度和横向加速度误差，通过PI控制调节转矩。文献[11]计算横摆角速度、质心侧偏角与参考值间的差值，用滑模控制计算出了总横摆力矩，以轮胎力最小来优化分配各个轮胎受力，控制效果好，但求解时间较长。文献[12]研究了基于滑转率的转矩控制，发现：在附着系数最大时，车辆动态特性最好，最佳滑转率在15%-20%之间；并根据滑转率的实际值和目标值间的差值对驱动轮力矩进行分配。文献[13]通过在基本前轮转向角上再增加一定的补偿角度，来改变前轮受到的侧向力，以提高车辆的操纵性和稳定性。

在特定的车辆实例中，针对某一个目标例如滑移率、横摆角速度、横摆力矩控制，上述研究都得到了相对满意的结果。但，控制策略的使用、控制参数的调整和补偿、动力学特性和动力学参数，以及电机的参数和选择千差万别，目前尚没有通用的参照可以使用。而且文献中的模型大多只包含车辆模型，把电机作为一个理想单元，没有详细的机电特性环节。本文在前期轮毂电机研究的基础上，针对后轮轮毂电机驱动的特定车辆，将汽车运动学模型、动力学模型、尤其是驱动电机机电特性模型集成起来，结合Ackermann转向模型，以车轮速度、电机速度作为控制变量和反馈变量，研究分布式驱动电动汽车的控制特性。

1 电动汽车运动及动力学模型

汽车整车动力学模型如图1所示。坐标系固连在车身上随着车身一起运动，原点O在车辆质心处，x轴为汽车的前进方向，即纵向方向。忽略车辆绕x轴的侧倾、绕y轴的俯仰和悬架特性，仅考虑车辆纵向平动、横向平动和在地平面中绕z轴的转动(横摆运动)，受力方面考虑地面对4个车轮的纵向摩檫力和横向摩擦力及车身受到的空气阻力，可得到纵向运动、横向运动和横摆转动的动力学方程组[14]：

图1 整车动力学及转向模型Fig. 1 Vehicle dynamics and turning

(Fx1+Fx2)cosδ-(Fy1+Fy2)sinδ+

(Fx3+Fx4)-f

(1)

(Fy1+Fy2)cosδ+(Fx1+Fx2)sinδ+(Fx3+Fx4)

(2)

A((Fx1+Fx2)sinδ+(Fy1+Fy2)cosδ)-

B(Fy2+Fx4)+

(3)

(Fy1-Fy2)sinδ+(-Fx3+Fx4))

其中，δ为前轮转向角，A为车辆质心到前轴的距离，B为车辆质心到后轴的距离，W为左右轮距，M为车辆质量，J为车辆转动惯量，v为车辆质心的速度，vx为车辆质心的纵向速度，vy为车辆质心的横向速度，ω为车辆的横摆角速度，Fxi、Fyi(i=1, 2, 3, 4)为各个车轮受到的纵向摩檫力和侧向摩檫力，f为空气阻力，且：

(4)

CA为复合空气阻力系数，与空气阻力系数、车辆正面迎风面积和空气密度有关。每个车轮中心沿着车轮纵向的速度由式(5)计算。其中,αi为车轮侧偏角。

(5)

当车轮横向力一定时，纵向力取决于车轮的滑转率。在滑转率很小时(对于干路面，滑转率小于0.1)，纵向力与滑转率成正比[15]，即：

(6)

vwi为车轮速度，vi为车轮中心速度平行于车轮平面的分量，Cx为车轮的纵向刚度。由于车轮的侧向弹性形变，车轮中心速度与车轮平面成一夹角，即车轮侧偏角，分别为：

(7)

当车轮侧偏角小于5°时，轮胎侧偏特性处于线性区，即车轮受到的垂直方向的力一定时，侧向力与侧偏角成正比[15]，如式(8)所示。其中，Cy为车轮的侧偏刚度，本文取轮胎魔术公式的线性段斜率值。

Fyi=-Cyai，i=1,2,3,4

(8)

假设θ为车辆横摆角，X、Y分别为质心在地面全局坐标系中的坐标。起始时间t= 0时，质心的坐标为(0，0)，即车辆处于原点处，这时横摆角为0；则车辆的运动轨迹为时间的函数：

(9)

2 电机驱动及控制

轮毂电机采用直流电机，直流电机产生的电磁转矩带动车轮旋转，同时克服由于内部摩擦产生的阻力和负载转矩，达到平衡；对电机而言，车轮和地面的摩擦力为负载；对车辆来说，该摩擦力就是车轮前进的驱动力。因此，机电耦合的车轮转动方程和直流电机的电枢回路电压平衡方程如式(10)所示：

(10)

其中，Te为电磁转矩，与电流成正比；J为车轮加电机的转动惯量；R为车轮半径；Ua(t)为电枢电压；w(t)为电机转速；La、Ra分别为电枢电路的电感和电阻；ia(t)为电枢电流；Ea为电枢反电动势；Fx为车轮驱动力；Bm、Ke、Kt分别为粘性摩擦系数、电势系数和转矩系数，由电机设计参数得出。

将公式(10)的两个方程分别进行拉氏变换得到控制模块中的传递函数：

Te=Jωs+Bmω+FxR

Ua=Laias+Raia+Keω

(11)

3 仿真分析

根据公式(1)-(11)搭建的Simulink控制模型如图2所示。图中，右下角为后轮3和后轮4 驱动电机模型。根据转角和预期的行驶速度，后轮3和后轮4的速度分配按照Ackerman模型进行，得到理想的轮速；和当前实际的轮速进行比较，得出预期的驱动力和转矩，作为负载转矩输入到各自的驱动电机中。两个电机均有转速反馈，形成车轮一级的控制；同时汽车的整体行驶速度也有反馈环节，见图2中左下角，形成具有两个轮速加一个行驶速度，即三个反馈环节的PID控制模型(后称为三环节PID模型)，使车辆按照要求的速度和转角行驶。车辆及直流电机的主要参数为：M=1 500;A=1.6;B=1.4;W=1.6；J=3 375;R=0.3;Ke=4.5;Kt=43;La=0.012;Ra=1.2;Bm=0.005。控制参数需要根据模型进行整定和优化。

为验证控制方法的有效，将三环节PID控制模型、一环节PID控制模型(即只有车辆行驶速度的反馈控制，没有轮毂电机速度反馈)和不加PID控制的初始模型进行了仿真分析和对比。为了方便分析，三环节PID控制模型的数据标记加后缀with PID and Motor, 一环节PID控制的标记加后缀with PID，第三组数据为无PID环节的原始模型，不加任何后缀，只有参数表示，例如speed。仿真模型中，在特定的行驶速度和转角下，理想的横摆角速度γd和侧向加速度αyd如式(12)所示[16]。其中，Kus为汽车的稳定性系数，由回归得出。本文的仿真分析路况为干性平坦路面。

(12)

3.1 直线行驶速度阶跃上升、缓慢升降状态

直线行驶仿真分成两种速度工况：一种情况为阶跃变化，速度在5 s(仿真时刻)时由原来的10 m/s (36 km/h)阶跃变化为16 m/s(58 km/h)，在10 s时由16 m/s(58 km/h)阶跃变化为26 m/s(94 km/h)；另一种情况是斜坡变化，在0-2 s内速度由10 m/s(36 km/h)斜坡升至30 m/s，并在3-5 s时间内保持该速度不变，之后在5-7 s的时间内速度从30m/s斜坡降低到20 m/s。以上两种预期速度状态下，三种控制方式的响应结果如图3所示。可以看出，三环节PID模型在响应速度和超调量方面的综合表现在三种模型中是较好的，能满足速度控制要求。

3.2 速度恒定，转角阶跃变化状态

转弯仿真时速度保持不变，转角分别在5 s和10 s时发生两次阶跃变化。在5 s时刻转角从0突变至0.08弧度，在10 s时刻转角从0.08弧度阶跃变化为0.16 弧度。三种控制模型在这种转角变化工况下的响应如图4所示。从图4可以看出，车辆的转动(转角的变化)需要产生一个横向加速度和横摆角速度，为维持能量的平衡会牺牲一部分行驶速度；如果不加控制来及时提高所需驱动力和驱动力矩，行驶速度就会降低(如图中Speed曲线)；加了一层PID控制后(图中Speed with PID曲线)，行驶速度最终不会降下来，但是在阶跃变化时刻有一个微小的向下波动，反应了转弯对行驶速度的干扰；在三环节控制PID模型中，由于有三个环节的协调控制，行驶速度向下的波动很最小，即形式速度受转角的干扰最小。

图5-6分别是横摆角速度和侧向加速度的控制响应曲线。从图中可以看出，三环节集成控制模型的横摆角速度和侧向加速度更接近理想值，其他两种模型都有较大的稳态误差。图7为该工况下的行驶轨迹。在图7中，因三环节控制模型的角速度和侧向加速度都更接近于理想值，因此其转弯半径最小、行驶距离最大。

3.3 转角正弦变化状态

转角正弦变化仿真工况设定为：转角正弦变化一个周期，频率为0.7 Hz，在第二个峰值处有400 ms的延迟，之后直线行驶。图8显示了这种工况下的速度变化情况，即转弯对行驶速度的干扰程度。从图8可以看出：转弯时产生的角速度和向心力对行驶速度有耦合作用，转角的变化引起了直线行驶速度的波动；三种模型相比较，三环节PID控制模型因转角变化引起的速度波动最小。图9为这种工况的横摆角速度响应，图10为侧向加速度响应曲线。图9-10的响应曲线表明：横摆角速度和侧向加速度峰值均低于理想值。需要说明的是，速度和转角的理想值是控制变量，是直接设定的，而横摆角速度和侧向加速度的理想值是利用经验公式(12)计算的，因此响应值和理想值相比只能作为一个参考，不能作为模型控制精度的评判，需要比较的是三个模型的响应特性。可以看出，三个模型的响应速度区别不大，且相位都有相同程度的滞后，这说明由于整个车辆的惯性，转角响应需要一定的时间，符合转弯的动力学特性。和一环节模型相比，三环节PID控制模型的横摆角速度和侧向加速度响应的超调量较小，表明波动较小，变化平稳；图中显示的只是车辆质心的响应特性，只能说明总体质心的运动状况。进一步的验证需要结合四个车轮尤其是驱动轮的动力响应特性。图11是正弦工况下的后轮(驱动轮3和驱动轮4)纵向驱动力和横向驱动力，图12是4个车轮的纵向速度，图13为后轮驱动电机的电磁转矩和负载转矩。从图11-12中可以看出，在正弦工况下，后轮的纵向驱动力和侧向驱动力变化比较平稳，没有突然的急升急降；后轮的纵向速度变化也比较平稳；相比之下，前轮的纵向速度在正峰值右侧减速时出现了一个小的波动和突起。轮2变化很小，可以忽略，轮1变化略大，变化范围大约0.2 m/s，为速度峰值的1%。分析原因，前轮为操纵轮，方向的变化从前轮开始，左转时前轮1的转弯半径最小，所需的横向力和角加速度最大，因此纵向速度受干扰最大。但前轮不是驱动轮，速度的变化是被动的，1%的波动对整车的稳定特性影响不大。从各轮的纵向速度也可以看出转弯时左右轮的差速状态，验证了模型的正确。图13是正弦工况下两个驱动轮的车轮载荷和电机输出转矩，可以看出，除了启动的瞬间外，轮毂电机的输出转矩和相应车轮所需转矩变化一致，能及时满足车轮转弯时的转矩要求，且转矩和载荷变化都很平稳，满足平稳驾驶的需求。唯一的问题是启动时刻转矩波动很大。车辆的启动特性较为特殊，需要针对电机的启动控制和特定车辆进行专门的研究，不在本文的讨论范围。

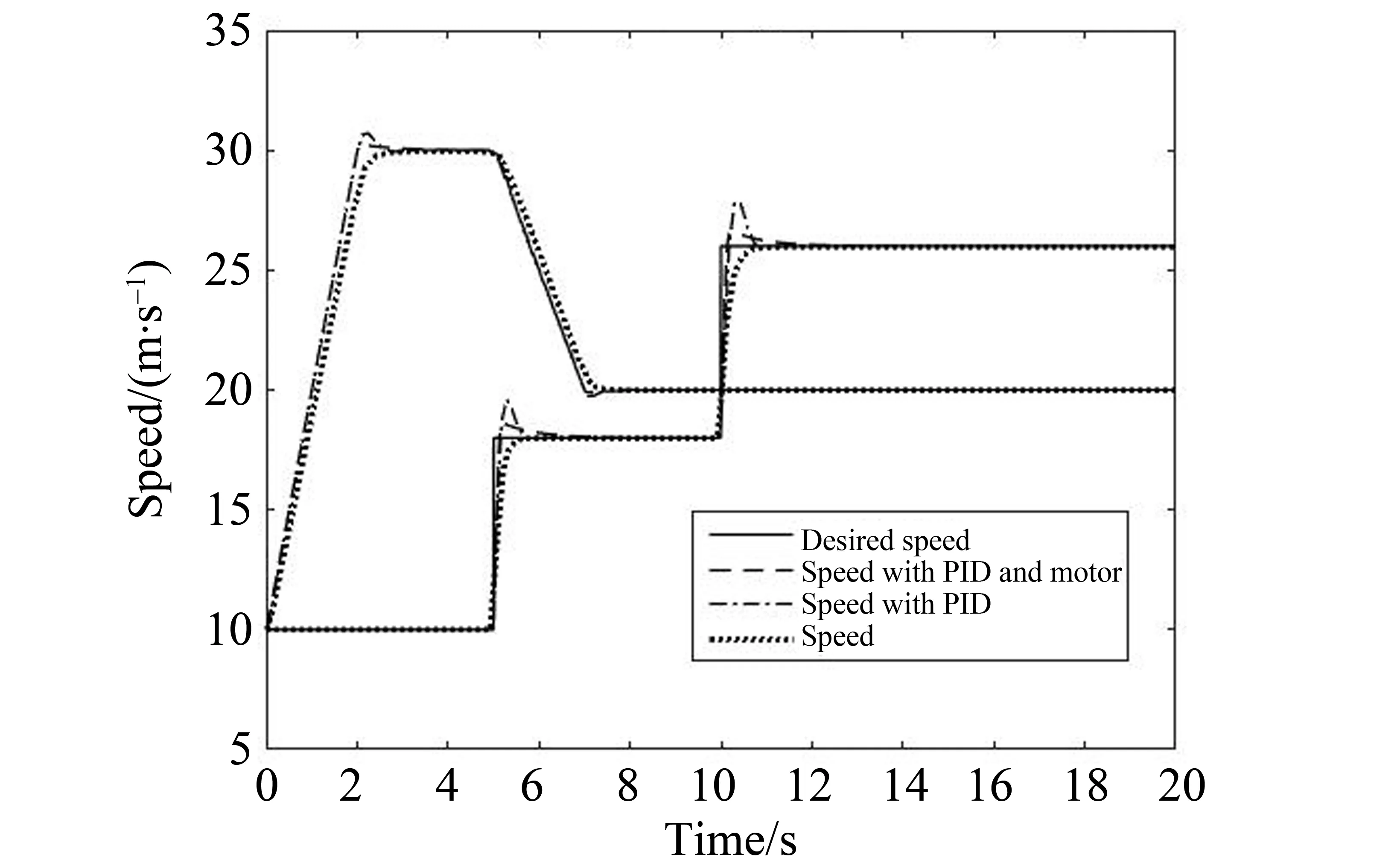
图3 直线行驶速度阶跃及缓慢升降Fig.3 Speed steps and slope changes

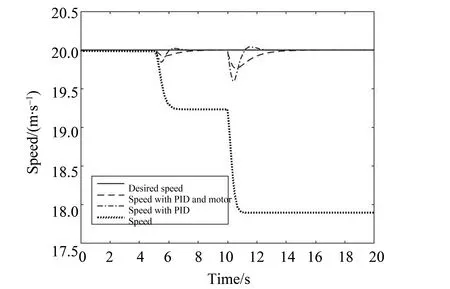
图4 转角阶跃变化—速度跟踪Fig.4 Speed under turning angle Steps

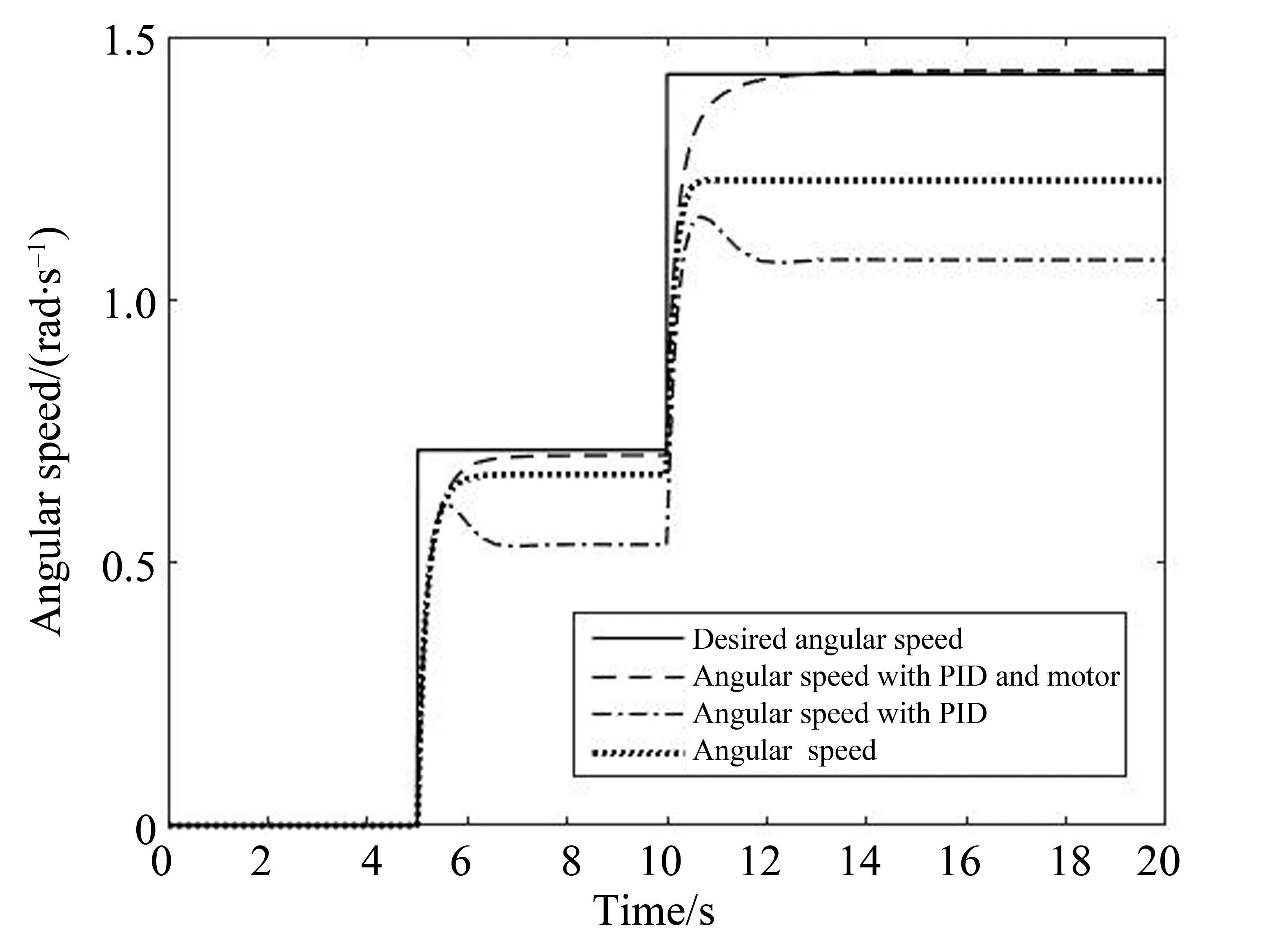
图5 转角阶跃变化—横摆角速度Fig.5 Angular speed under turning angle steps

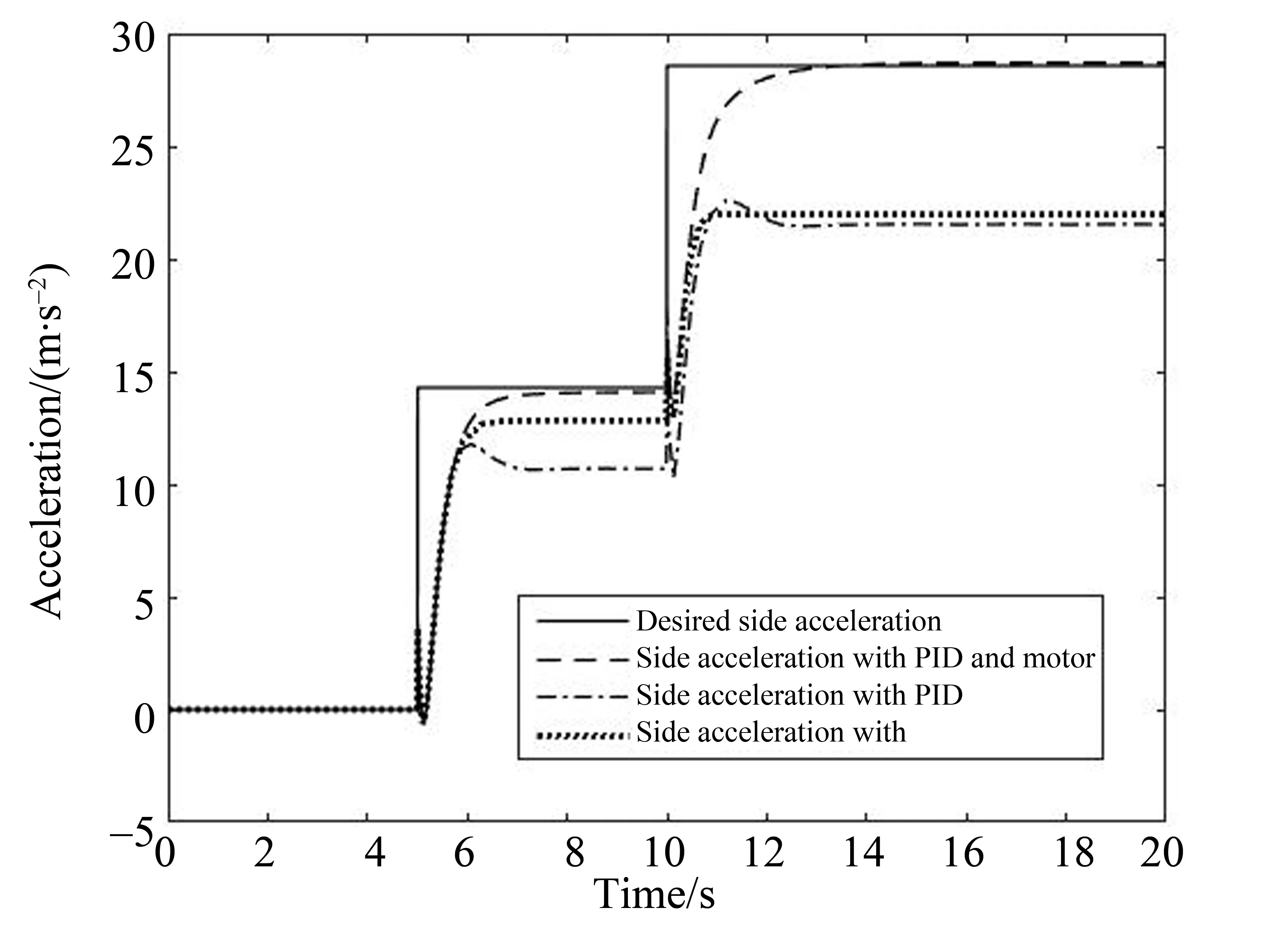
图6 转角阶跃变化—侧向加速度Fig.6 Side acceleration under turning angle steps

图7 转角阶跃变化—行驶轨迹图Fig.7 Drived path under turning angle steps

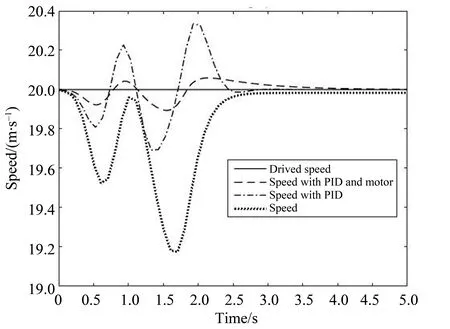
图8 转角正弦变化—速度控制Fig.8 Speed response under turning angle sine

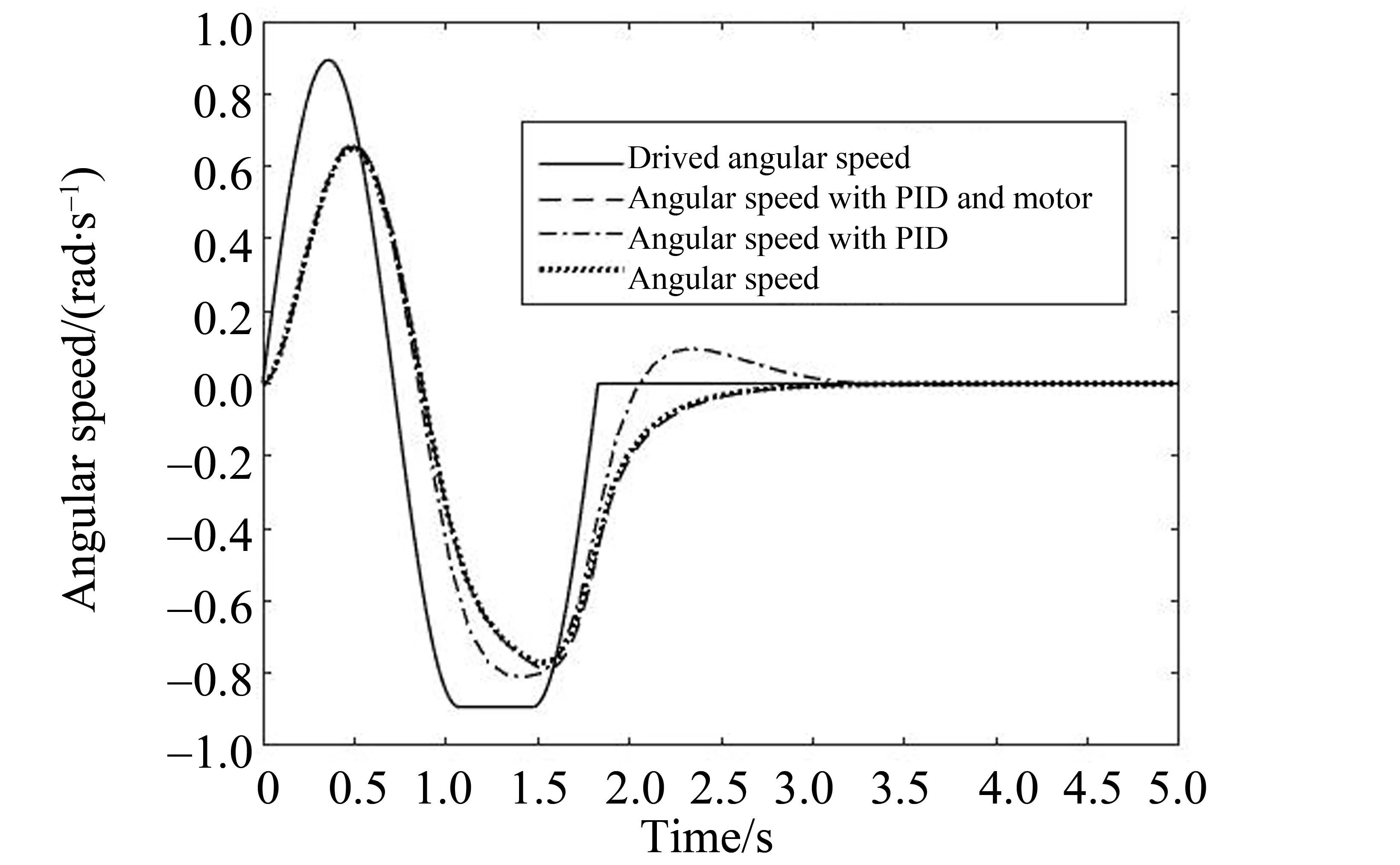
图9 转角正弦变化—横摆角速度Fig.9 Angular speed under turning angle sine

图10 转角正弦变化—侧向加速度Fig.10 Side acceleration under turning angle sine

4 结 论

本文针对后轮轮毂电机驱动的车辆，将电机机电特性模型结合到汽车整车运动学和动力学模型中，形成一个包含电机参数和车辆行驶参数的集成控制模型，更真实的模拟整车的动力学特性和驱动特性。控制模型中以车轮行驶速度、两个轮毂电机速度作为控制和反馈变量，形成三环节PID控制模型；以车辆的预期行驶速度和转弯角度作为控制和跟踪的目标；使用Ackermann模型进行转弯时左右轮的速度分配，根据实际转速和预期转速确定每个轮子所需的驱动转矩。四种工况下的仿真分析结果表明：

图11 转角正弦变化—后轮纵向和侧向驱动力Fig.11 Bear wheel driving force under turning angle sine

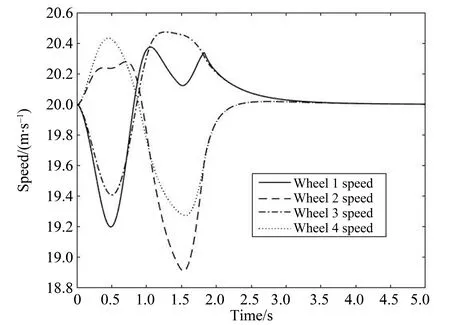
图12 转角正弦变化—四轮的纵向速度Fig.12 Forward speeds under turning angle sine

图13 转角正弦变化—电机转矩及车轮驱动载荷Fig.13 Motor toque and Load toque under turning angle sine

1)在直线行驶速度突然变化和速度缓慢变化两种行驶状态下，三环节PID控制模型和一环节控制模型的响应速度都比较快，但三环节模型的超调量最小，综合性能最佳，可以满足直线行驶时车辆突然加速和缓慢加减速的要求；

2)在行驶速度恒定转角阶跃变化(突然转向)工况下，侧向加速度的产生需要一部分动力，行驶速度会受到影响，三环节PID模型的行驶速度损失最小；在阶跃变化的瞬间经历微小的波动后，速度立刻恢复到预期的速度；在横摆角速度和侧向加速度方面，三种模型的响应速度差别不大，但就稳态误差而言，三环节控制模型远小于其他两种模型，因此转弯半径最小，行驶距离也最长；

3)在行驶速度恒定转角正弦变化工况下，三环节PID控制模型速度波动最小，横摆角速度和侧向加速度的超调量较小，四轮驱动力变化比较平稳。除了启动时刻，电机输出转矩变化平稳。