基于交互间隙法的内部Neumann反散射问题∗

刘立汉，崔晓英，蔡静秋

(重庆师范大学数学科学学院, 重庆401331)

外部反散射问题是一类典型的反散射问题。如一个物体被平面入射波或者点源散射，其反问题是从远场数据或者近场数据重构散射物体的位置、形状及其物理性质。这样的问题出现在各种医学成像、超声波断层、材料科学、无损探测、雷达、遥感和地震勘测等领域，见文献[1-4]。本文我们研究如何从位于腔体内部的点源测量数据来重构腔体的位置、形状及其物理性质，即内部反散射问题，这类问题出现在工业应用中的非结构探测，如检测聚变反应堆的结构完整性，见文献[5]。近年来，内部反散射问题已经吸引了很多的研究者，在文献[5]中，Jakubik和Potthast通过电位法和量程检验得到Cauchy问题的解，利用这些解来研究一些声学腔体的完整性；之后，线性采样方法被用来处理部分涂层的腔体和可穿透性腔体的内部反散射问题，如Cakoni和Liu的文献[6]、Qin和Liu的文献[7]、Cakoni、Colton和Meng的文献[8]、Liu的文献[9]；此外，因式分解法(见文献[10])和近场成像法(见文献[11])也被用来决定腔体的形状；类似地，Qin和Cakoni的文献[12]使用的是非线性积分方程方法，Zeng、Suarez和Sun的文献[13]使用的是分裂法。

本文我们用另一个采样方法，即交互间隙方法来处理内部反散射问题，这种方法最早由Colton和Haddar提出来的。正如文献[4]中标注的那样，这种方法有两个优点，一是不需要散射物体的物理性质的先验知识；二是它避免对格林公式的背景介质的计算；但交互间隙方法的一个显著特点是使用柯西数据。在文献[14]，Cakoni等一些人进一步分析了该方法对Maxwell方程和层状介质的影响，在文献[15]中，Shifrin和Shushpannikov应用交互间隙方法来识别弹性固体的球状缺陷，在文献[16]中，Monk和Selgas采用交互间隙方法处理反流-固体耦合问题。

本文结构如下：首先，我们阐述了内部反散射问题相关的数学模型。然后，根据线性积分方法介绍交互间隙方法，并研究相应的定理和结论。最后，对交互间隙方法进行了数值验证，并且我们提出的数值例子显示了交互间隙方法的可行性。

1 反散射问题

Δu+k2n(x)u=0,x∈D{x0},

(1)

这里的υ是曲线的单位向外法向量，k是波数。我们假定B有有限多个组合并且这个曲线穿过B,n(x)是不连续且分段光滑的，u=ui+us是总场，us是散射场。从文献[8]，我们可以得到，ui,us满足交互关系，即

us(x,x0)=us(x0,x),

ui(x,x0)=ui(x0,x),

我们注意到ui可以被写作

ui(x,x0)=Φ(x,x0)+Φs(x,x0)=G(x,x0),

x∈R2

对x≠x0,这里的Φ(x,x0)是Helmholtz方程的基础解，且

ΔG+k2n(x)G=-δ(x-x0),

并且适合Sommerfeld辐射条件，即

r=|x|

令

U={u∂Du∈H1(D{x0}):

Δu+k2u= 0,x∈D{x0};

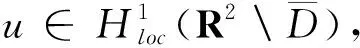
其中g是一个连续函数，由文献[17]中可知，上述方程有唯一解。

现在让Ω是D中的一个有界Lipschitz域，因此DC⊂Ω⊂D,这里的DC表示C的内部。本文中的散射问题，我们需要的是从∂Ω的总场u的柯西数据来决定散射物体的形状。

定义1 设非零的数k2∈C,若存在一个非平凡的解u∈H1(D),满足

Δu+k2n(x)u=0,x∈D,

则称k2是-Δ在D内的一个广义的Neumann特征值。

接下来，证明反散射问题的唯一性定理。

定理1 若k2不是Ω中的一个广义Neumann特征值，则∂D被C上的所有点源x0在∂Ω上的散射场us(x,x0)唯一确定。

证明假定D1≠D2是包含Ω的两个有界区域，并且ui,us分别是方程(1)的点源G(x,x0)的区域D被D1,D2替代后的解。

Δvs+k2n(x)vs=0,x∈Ω,

(i)Bε,x1∩D1≠∅,

(ii)Bε,x1∩D2⊂D2,

因此yn∈Bε,x1,且x1∈Bε,x1⊂D2∉∂D2.

又由于k2不是Neumann特征值，则由文献[1, 17]可知，方程(1)满足解的适定性，则存在一个常数c1>c0>0,有

对所有的n≥1均成立，这里的Γ表示∂D1⊂Bε,x1的子集。

另一方面，证明从x1出发的入射波是有界的。由于在∂D上，有

则

又由交互关系可得

令D*是一个有界Lipschitz域，因此D0⊂D*且Bε,x1∩∂D*=Γ,令Γ1=∂D*Γ,则x1到Γ1的距离大于h,因此存在一个常数c2>0,使得

ui(x,x1)=Φ(x,x1)=

则

▽ui(x,x1)=

于是当x→x1时，

▽ui(x,x1)→∞

矛盾，所以D1=D2。

2 交互间隙法

在这一部分，我们利用交互间隙法来重构这个腔体的位置及其形状。首先定义两个空间

(i) 对于一个无界的开区域，定义

(ii) 定义

U*={u|u是方程(1)的解且

ui=G(x,x0),x0∈C}

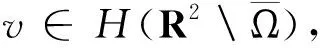
(2)

Rv(x0)=R(u,v)

(3)

下面，证明如果k2不是DC内的一个广义的Neumann特征值，则R是单射且有稠密值域。对于接下来的讨论，我们定义单层势能vg

(4)

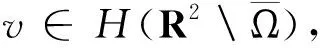
R(u,v)=0

则根据格林公式和边界条件有

即

令w是下列方程的解，即

Δw+k2n(x)w=0,x∈D;

由于k2不是广义的Neumann特征值，则上述方程在H1(D)中有唯一的解，且它连续依赖于ν。

又对∀u∈U*,u=us+G(·,x0),有

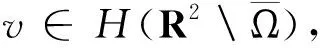
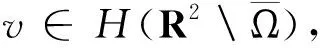
(Rv,φ)=0

由(2)式和R的双线性性，可得

0=R(h,v)=

Δh(x)+k2h(x)=0

Δh(x)+k2h(x)=0

且k2不是一个广义的Neumann特征值，则在Dc内h(x)=0。由单层势能的跳跃关系有

则算子R的稠密性得证。

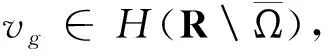
R(u,vg)=R(u,Φz)

(5)

此处Φz=Φ(·,z),z∈Ω∘(Ω∘是Ω的内部)。特别地，我们将说明如何使用这个函数g来描述∂D的特征。这个交互间隙法的优点在于对非均匀腔体，只需要基本解，相比于其他定性方法如线性抽样方法，需要背景格林函数，而这些函数要么是未知的，要么是很难计算的。

一般来说，这个积分方程(5)无解，然而如果k2不是Dc内的广义的Neumann特征值，它可能提供了积分方程(5)的近似解的可能性。接下来证明本篇论文的主要结论。

定理4 假定k2不是Dc内的广义的Neumann特征值，则有

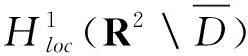
且

R(u,vgn-Φz)=

由于u∈U*,即u是方程(1)的解，即∂υu=0,则

(6)

vgn→Φz

R(u,vgn)→R(u,Φz)

即

且

R(u(·,x0),Φz)=

(7)

R(u(·,x0),Φz)=v(x0)+

再通过格林公式有

R(u(·,x0),Φz)=v(x0)-Φ(z,x0)

由式(7)可知，v(x0)-Φ(z,x0)作为Δu+k2n(x)u=0在DC内的解可以是连续的。

另一方面，

R(u(·,x0),vgn)=

又u∈U*由边界条件可得

假定存在一个数列{gn},gn∈L2(C),对∀u∈U*,当n→∞时，有

R(u(·,x0),vgn)→R(u(·,x0),Φz)

又由于当n→∞时，对∀x0∈C,有vgn→f, 则

∂υvgn-∂υf=∂υ(vgn-f)→0

即对∀x0∈C,当n→∞时，有∂υvgn→∂υf,则当n→∞时，有

有

Δw+k2nw=0,x0∈DC；

3 数值例子

在这一部分，我们将给出几个数值例子来验证我们前面两部分理论结果的有效性。在接下来的例子中，我们选择n=1.2,k=5。

利用交互间隙法来重构腔体的边界∂D的步骤如下：

(i)选一个包含未知腔体的样本点区域。在我们的例子中，样本区域为[-1,1]2。

(ii)对于每个样本点z,解如下正则化型的数据方程

(iii)计算指示函数I(z)。

(iv)描点画图I(z)。

第一个例子，我们考虑重构一个半径为0.5的圆，分没有噪声和带1%噪声两种情况，结果分别见图1(a)和1(b)。

第二个例子，我们考虑重构一个长为0.8的正方形，结果分别见图2。第三个例子，我们考虑重构一个长轴长为1，短轴长为0.8的椭圆，结果分别见图3。

如上的数值例子说明我们提出的交互间隙法来重构腔体的边界∂D是一种有效的算法。

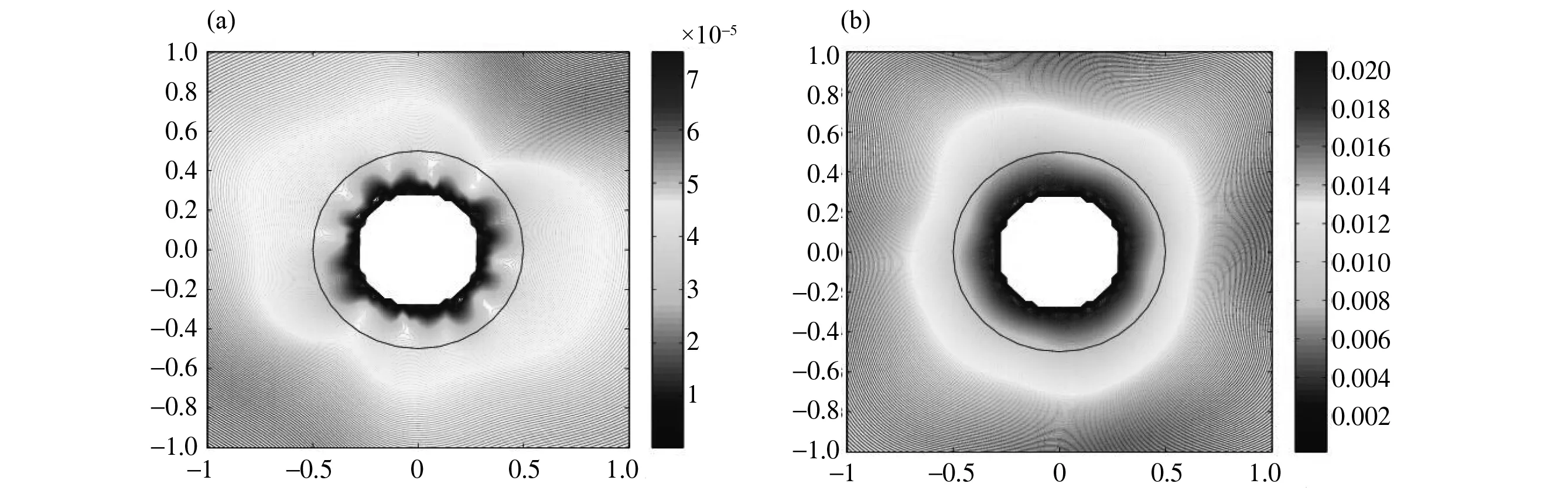
图1 (a) 重构半径为0.5的圆(无噪音) 图1(b) 重构半径为0.5的圆(有噪音)Fig.1 (a) Reconstruct a circle of radius 0.5(no noise) (b) Reconstruct a circle of radius 0.5(1% noise)

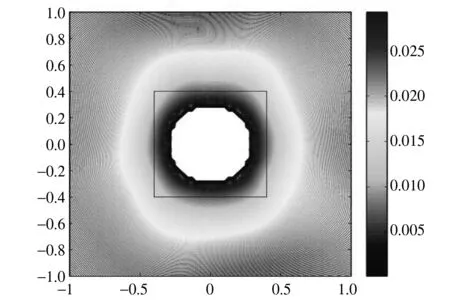
图2 重构边长为0.8的正方形Fig.2 Reconstruct a square of length 0.8

图3 重构长轴为1，短轴为0.8的椭圆Fig.3 Reconstruct an ellipse of x-axis 1, y-axis 0.8