“8”字图的匹配能级和Hosoya指标全排序∗

马海成，刘小花

(青海民族大学数学与统计学院，青海 西宁810007)

本文仅考虑有限无向的简单图。设G是有n个点的图，G的一个匹配是指G的一个生成子图, 它的每个分支或是孤立点或是孤立边。 恰有k条边的匹配称为k匹配。在文[1]中图G的匹配多项式定义为：

这里m(G,k)是G中的k-匹配的数目。为了方便，本文中有时将μ(G,x)简记为μ(G)。

定义1 设λ1,λ2,…,λn是图G的匹配多项式的所有根，定义它的匹配能级为：

匹配能级的概念衍生自是图的能级，所谓图的能级是这个图的谱的绝对值的和，即所有特征根的绝对值的和。在Hückel分子轨道理论中，共轭碳氢化合物的分子的π-电子能量水平近似地等于该分子图的能级。对图的能级已有了大量的研究，见专著[5]。由于无圈图的特征多项式等于匹配多项式[1]，故在无圈图上，能级和匹配能级是一致的。自从2012年Gutman和Wagner在文[4]中提出图的匹配能级的概念以来，对这个主题已经有了大量的研究，文[4]中指出在所有n阶图中，匹配能级最小的是空图，最大的是完全图, 也确定了匹配能级最小和最大的连通单圈图。文[6-7]中确定了匹配能级最大和最小的连通双圈图。 文[8-9]中确定了匹配能级最大和最小的连通三圈图。文[10]中确定了所有κ-连通图中的匹配能级最大的图和所有χ-色图中匹配能级最大的图等等。关于匹配数目的研究参见[11-13]。纵观这些研究结果，主要都集中在对给定的一类图刻画其匹配能级达到极值的图，但很少有文献对一类图的匹配能级给一个完全的排序，在这篇文章中，我们对一类所谓的“8”字图做这样的工作，给出了点数相同的“8”字图之间匹配能级的一个完全排序。作为推论，也给出这些图的Hosoya指标的一个完全排序。

以Pn，Cn，Kn分别表示n个点的路、圈和完全图。以G∪H表示两个图G和H的并图。 我们把形似“8”字的图称为8-字图，它是圈Ca+1上的一点和圈Cb+1上的一点粘结后得到的图(见图1)，记为记∞(a,b)。 显然有∞(a,b)≅∞(b,a)。在文中没有说明的记号和术语参见文[1]。

图1 “8-”字图∞(a,b)(a≥2,b≥2)Fig. 1 The 8-shape graphs ∞(a,b)(a≥2,b≥2)

1 若干引理

引理1[1]设图G有k个连通分支G1,G2,…,Gk，则

μ(G,x)=μ(G1,x)μ(G2,x)…μ(Gk,x)

引理2[1]设G是一个图，u∈V(G)，e=uv∈E(G)，则

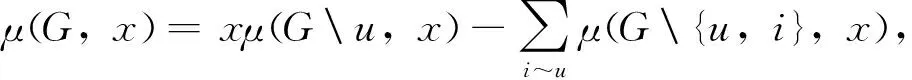
(ii)μ(G,x)=μ(Ge,x)-μ(G{u,v},x)。

引理3 设Pn是n个点的路，则

μ(Ps+t)=μ(Ps)μ(Pt)-μ(Ps-1)μ(Pt-1)

证明由引理2(ii)，结论显然成立。

引理4设Pn是n个点的路，k使下图有意义的整数，则

μ(Ps)μ(Pt)-μ(Ps-k)μ(Pt+k)=

μ(Ps-1)μ(Pt-1)-μ(Ps-k-1)μ(Pt+k-1)

证明由引理3，μ(Ps+t)=μ(Ps)μ(Pt)-μ(Ps-1)μ(Pt-1)，μ(Ps+t)=μ(Ps-k)μ(Pt+k)-μ(Ps-k-1)μ(Pt+k-1)，两式相减便得上式。

引理5[4]设G是一个图，则

这里m(G,k)是G中的k-匹配的数目。

G1G2⟹ME(G1)

引理6 设G1,G2是两个n阶图，如果存在一个m阶图H，满足

μ(G1)-μ(G2)=tμ(H),(t>0)

则

(i)n-m是一个偶数；

(ii) 如果n-m≡0(mod 4), 则ME(G1)>ME(G2)；

(iii) 如果n-m≡2(mod 4), 则ME(G1)

证明

(i)由于多项式μ(Gi,x)(i=1,2)中xn-(2k-1)的系数均为零，则多项式μ(G1,x)-μ(G2,x)中xn-(2k-1)的系数也为零。于是tμ(H)的首项txm必定是形如txn-2k，对某个整数k。 故n-2k=m。 则n-m是一个偶数。

(ii) 不妨设n=m+4k，

μ(G1)=xn-m(G1,1)xn-2+…+

m(G1,2k)xm-m(G1,2k+1)xm-2+…,

μ(G2)=xn-m(G2,1)xn-2+…+

m(G2,2k)xm-m(G2,2k+1)xm-2+…,

μ(H)=xm-m(H,1)xm-2+…

由于μ(G1)=μ(G2)+tμ(H),比较系数得

所以G1≻G2故ME(G1)>ME(G2)。

(iii) 不妨设n=m+4k+2，

μ(G1)=xn-m(G1,1)xn-2+…-

m(G1,2k+1)xm+m(G1,2k+2)xm-2+…,

μ(G2)=xn-m(G2,1)xn-2+…-

m(G2,2k+1)xm+m(G2,2k+2)xm-2+…,

μ(H)=xm-m(H,1)xm-2+…

由于μ(G1)=μ(G2)+tμ(H),比较系数得

m(G1,s)=

所以G1G2，故ME(G1)

2 主要定理及证明

定理1 对“8-”字图∞(a,n-a-1)(a≥2), 有

(i)当n=4k, 则

ME(∞(3,4k-4))>ME(∞(5,4k-6))>…>ME(∞(2k-1,2k))=ME(∞(2k,2k-1))>ME(∞(2k-2,2k+1))>…>ME(∞(4,4k-5))>ME(∞(2,4k-3))

(ii)当n=4k+1, 则

ME(∞(3,4k-3))>ME(∞(5,4k-5))>…>ME(∞(2k-1,2k+1))>ME(∞(2k,2k))>ME(∞(2k-2,2k+2))>…>ME(∞(4,4k-4))>ME(∞(2,4k-2))

(iii) 当n=4k+2, 则

ME(∞(3,4k-2))>ME(∞(5,4k-4))>…>ME(∞(2k-1,2k+2))>ME(∞(2k,2k+1))>ME(∞(2k-2,2k+3))>…>ME(∞(4,4k-3))>ME(∞(2,4k-1))

(iv) 当n=4k+3 则

ME(∞(3,4k-1))>ME(∞(5,4k-3))>…>ME(∞(2k-1,2k+3))>ME(∞(2k+1,2k+1))>ME(∞(2k,2k+2))>ME(∞(2k-2,2k+4))>…>ME(∞(4,4k-2))>ME(∞(2,4k))

证明

(i)证明分以下两步：

第一步，证明对正整数3≤s≤k,有

ME(∞(2s-3,4k-2s+2))>

ME(∞(2s-1,4k-2s))

(1)

由引理2-4得，

μ(∞(2s-3,4k-2s+2))-

μ(∞(2s-1,4k-2s))=

xμ(P2s-3)μ(P4k-2s+2)-

2μ(P2s-4)μ(P4k-2s+2)-2μ(P2s-3)μ(P4k-2s+1)-

[xμ(P2s-1)μ(P4k-2s)-

2μ(P2s-2)μ(P4k-2s)-2μ(P2s-1)μ(P4k-2s-1)]=

x[μ(P2s-3)μ(P4k-2s+2)-μ(P2s-1)μ(P4k-2s)]+

2[μ(P2s-2)μ(P4k-2s)-μ(P2s-4)μ(P4k-2s+2)]+

2[μ(P2s-1)μ(P4k-2s-1)-μ(P2s-3)μ(P4k-2s+1)]=

x[μ(P4k-4s+5)-μ(P2)μ(P4k-4s+3)]+

2[μ(P2)μ(P4k-4s+4)-(P4k-4s+6)]+

2[μ(P2)μ(P4k-4s+2)-μ(P4k-4s+4)]=

-xμ(P1)μ(P4k-4s+2)+2μ(P1)μ(P4k-4s+3)+

2μ(P1)μ(P4k-4s+1)=

x2μ(P4k-4s+2)=μ(2K1∪P4k-4s+2)

因此，由引理6(ii) 得到不等式(1)。

第二步，证明对正整数2≤s≤k,有

ME(∞(2s,4k-2s-1))>

ME(∞(2s-2,4k-2s+1))

(2)

由引理2-4得，

μ(∞(2s,4k-2s-1))-

μ(∞(2s-2,4k-2s+1))=

xμ(P2s)μ(P4k-2s-1)-2μ(P2s-1)·

μ(P4k-2s-1)-2μ(P2s)μ(P4k-2s-2)-

[xμ(P2s-2)μ(P4k-2s+1)-2μ(P2s-3)μ(P4k-2s+1)-

2μ(P2s-2)μ(P4k-2s)]=

x[μ(P2s)μ(P4k-2s-1)-μ(P2s-2)μ(P4k-2s+1)]+

2[μ(P2s-3)μ(P4k-2s+1)-

μ(P2s-1)μ(P4k-2s-1)]+

2[μ(P2s-2)μ(P4k-2s)-μ(P2s)μ(P4k-2s-2)]=

x[μ(P2)μ(P4k-4s+1)-μ(P4k-4s+3)]+

2[(P4k-4s+4)-μ(P2)μ(P4k-4s+2)]+

2[μ(P4k-4s+2)-μ(P2)μ(P4k-4s)]=

xμ(P1)μ(P4k-4s)-2μ(P1)μ(P4k-4s+1)-

2μ(P1)μ(P4k-4s-1)=

-x2μ(P4k-4s)=-μ(2K1∪P4k-4s)

由引理6(iii)得到不等式(2)。

(ii) 证明分以下三步。

第一步，证明对正整数3≤s≤k,有

ME(∞(2s-3,4k-2s+3))>

ME(∞(2s-1,4k-2s+1))

(3)

与(i)的第一步类似可得到，

μ(∞(2s-3,4k-2s+3))-

μ(∞(2s-1,4k-2s+1))=

μ(2K1∪P4k-4s+3)

由引理6(iii)得到不等式(3)。

第二步，证明不等式

ME(∞(2k-1,2k+1))>ME(∞(2k,2k))

(4)

μ(∞(2k-1,2k+1))-μ(∞(2k,2k))=

xμ(P2k-1)μ(P2k+1)-

2μ(P2k-2)μ(P2k+1)-2μ(P2k-1)μ(P2k)-

[xμ(P2k)μ(P2k)-2μ(P2k-1)μ(P2k)-

2μ(P2k)μ(P2k-1)]=

x[μ(P2k-1)μ(P2k+1)-μ(P2k)μ(P2k)]+

2[μ(P2k-1)μ(P2k)-μ(P2k-2)μ(P2k+1)]=

x[μ(P2)-μ(P1)μ(P1)]+

2[μ(P1)μ(P2)-μ(P3)]=μ(K1)

所以，由引理6(ii)得到不等式(4)。

第三步，证明对正整数2≤s≤k,有

ME(∞(2s,4k-2s))>

ME(∞(2s-2,4k-2s+2))

(5)

与(i)的第二步类似可得到，

μ(∞(2s,4k-2s))-

μ(∞(2s-2,4k-2s+2))=

-μ(2K1∪P4k-4s+1)

由引理6(iii)得到不等式(5)。

(iii)、(iv)证明与(i)或(ii)类似，略。

下面的两个推论是定理1的直接推论。

推论1 设“8-”字图∞(a,b)(a≥2,b≥2)满足a+b+1=n，则它的Hosoya指标排序为

(i) 当n=4k, 则

Z(∞(3,4k-4))>Z(∞(5,4k-6))>…>

Z(∞(2k-1,2k))=Z(∞(2k,2k-1))>

Z(∞(2k-2,2k+1))>…>

Z(∞(4,4k-5))>Z(∞(2,4k-3))

(ii) 当n=4k+1, 则

Z(∞(3,4k-3))>Z(∞(5,4k-5))>…>

Z(∞(2k-1,2k+1))>

Z(∞(2k,2k))>Z(∞(2k-2,2k+2))>…>

Z(∞(4,4k-4))>Z(∞(2,4k-2))

(iii) 当n=4k+2, 则

Z(∞(3,4k-2))>Z(∞(5,4k-4))>…>

Z(∞(2k-1,2k+2))>

Z(∞(2k,2k+1))>Z(∞(2k-2,2k+3))>

…>Z(∞(4,4k-3))>Z(∞(2,4k-1))

(iv) 当n=4k+3 则

Z(∞(3,4k-1))>Z(∞(5,4k-3))>

…>Z(∞(2k-1,2k+3))>

Z(∞(2k+1,2k+1))>Z(∞(2k,2k+2))>

Z(∞(2k-2,2k+4))>…>

Z(∞(4,4k-2))>Z(∞(2,4k))

推论2 在所有n个点的“8”-字图中，∞(3,n-4)的匹配能级最大，∞(2,n-3)的匹配能级最小。类似地，∞(3,n-4)的Hosoya指标最大，∞(2,n-3)的Hosoya指标最小。