基于EKF 与TLS动态模糊神经网络算法∗

张彩霞

(佛山科学技术学院自动化学院，广东 佛山 528000)

模糊理论和神经网络技术是近几年来人工智能研究较为活跃的两个领域。从本质上来说，模糊逻辑系统就是一个基于IF-THEN规则的系统，而此处的模糊规则实际上来自人类的学习。更准确地说，设计一个模糊系统是采用主观的方式来表达设计者的知识。由于在现实生活中不存在一种正式的和有效的知识获取方式，因此对于设计者来说，即使他是领域专家，要完成复杂系统所有的输入输出数据的检查以找到一组合适的规则也是很难的。而从神经网络的角度来看，由于神经网络是一个黑箱，不具有明确的物理意义，因此，专家对研究对象的部分知识无法应用到神经网络中。训练时，只能任选初值，导致训练容易陷入局部极限小点。但是，一个模糊神经网络却有明确的物理意义，专家知识很容易结合到模糊神经网络中，这对提高收敛速度、缩短训练时间是很有帮助的。因此，模糊神经网络不仅吸取了模糊逻辑和神经网络二者的优点，还克服了各自具有的缺点。正因如此，模糊神经网络成为当前研究的一个热点，并形成了一个较为完善的体系[1]。

1 动态模糊神经网络算法

1.1 径向基(RBF)神经网络

我们提出的算法是D-FNN算法，它的激活函数是高斯函数。一个具有r个输入和一个输出的RBF神经网络，该网络可以看成如下形式的映射f:Rr→Rs：

(1)

如果采用高斯函数而不考虑偏置量，则式(1)可以写为如下的函数：

(2)

如果把各高斯函数的输出归一化，则RBF网络可以产生如下归一化的输出响应。

(3)

由于高斯函数具有各向同性，因此以高斯函数作为激活函数的神经网络称为径向基(RBF)神经网络。

1.2 总体最小二乘修剪技术

在学习进行时，检测到不活跃的模糊规则并加以剔除，则可获得更为紧凑的D-FNN结构。在本文中我们将采用TLS方法作为修剪技术来选择重要的模糊规则[2]。

总体最小二乘(TLS)方法是用来补偿线性参数估计问题中数据误差的一种技术。考虑如下形式的线性参数估计问题：

D=Hθ+E

(4)

在解决这个问题时，普通的最小二乘(LS)方法假定矩阵H(在参数估计问题中通常称为测量矩阵)与误差无关并且所有的误差被限制在观测向量D中。基于TLS的子集选择方法由Van Huffel和Vandewalle在文献[3]和文献[4]中提出。这里借用该方法从一个给定的规则库中提取最重要的模糊规则。把SVD(奇异值分解)应用于一个定义为[H·D]扩展的矩阵，即：

(5)

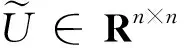
(6)

其中,b≤rank[HD]对应于要选择的模糊规则数。运用QR列主元计算：

bv-b

(4)

bv-b

(7)

可以证明：

(8)

ITLS=[ITLS1,ITLS2,…,ITLSv]T=

(9)

b个最重要的模糊规则的结论部分可以通过如下的简化方程得到：

(10)

(11)

1.3 D-FNN参数调整方法

EKF(扩展的卡尔曼滤波)是基于梯度的在线学习算法，同其他基于梯度的在线算法相比，EKF可以加快收敛速度。作一种非线性更新算法，EKF方法可以用来调节D-FNN的所有参数。实验结果表明，高斯中心对系统性能影响不大，因此只对高斯宽度进行更新。结果参数的更新是线性的，而高斯宽度的更新是非线性的，可以用EKF作如下优化：

i=1,2,…,n

(12)

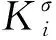
j∈{ 1,2,…,u}

(13)

其中，Cj和wj分别是中心和第j个RBF单元的权值，ψj是第j个归一化层的输出[8]。

需要强调的是，KF或EKF算法用于D-FNN，当一条规则产生/去除或者宽度有任何的调整时，将产生额外的计算负担，即在这些情况下，迭代将必须从第一个样本开始。

2 实验结果与分析

我们用D-FNN来进行Mackey-Glass混沌时间序列预测。以下的仿真在D-FNN中使用串-并行方法。

Mackey-Glass混沌时间序列[9]是Mackey等在1977年所提出的一个模型，用于描述白血病发病时，血液中白细胞的数量变化。其方程如下所示：

图1 Mackey-Glass时间序列预测Fig.1 Mackey-Glass time series prediction

(14)

当τ<17时，表现出周期性，而当τ>17时，方程(14)表现出混沌行为，且τ值越大混沌现象越严重。对这种时间序列的预测是一个被许多研究者研究过的典型问题。为了能够在相同的基础上进行比较，参数选择为：a=0.1、b=0.2和τ=17。预测模型表示如下：

x(t+p)=

f[x(t),x(t-Δt),x(t-2Δt),x(t-3Δt)]

(15)

图1描绘了从t=118到t=617的训练结果和前6步预测结果。选择不同参数，将得到两种不同的模糊神经网络结构。选择Δt=6以及p=50、80，为了方便比较，用归一化的均方根误差或无量纲指数(NDEI)来评估泛化能力。当p分别等于85和50时，D-FNN、ANFIS[10]、RAN[11](资源分配网络)、RANEKF[12](扩展卡尔曼滤波的资源分配网络)及M-RAN[7](最小资源分配网络)的结果比较列于表1和表2中。

表 1 p=85时，D-FNN与ANFIS的泛化能力比较Table 1 Comparison of generalization ability of D-FNN and ANFIS at p=85

表2 p=50时，D-FNN、RAN、RANEKF和M-RAN泛化能力比较Table 2 Comparison of generalization ability of D-FNN,RAN,RANEKF and M-RAN at p=50

比较结果显示，即使D-FNN有更多的可调参数，它的性能也并没有ANFIS好。原因是ANFIS通过迭代学习的方式训练，从而可以达到整体的最优解。而D-FNN只能获得次优的结果。然而，与RAN、RANEKF及M-RAN(它们也只能得到次优解)相比，D-FNN结构小而泛化能力更强。

当一个模糊系统、神经网络用于函数逼近问题时，一般的形式如下：

(16)

其中，wi是权值，Ri(X,wi)是基函数，u是基函数的个数。一旦Ri(X,wi)被选定，权值的选择就可以用线性代数中的标准方法求解[13]。

显然，我们所提出的D-FNN属于选择依赖于参数可变的自变适应基函数，从而获得最佳逼近和新的数据加入后，将相应地补充新的基函数的结合，只是基函数的参数调整并没有用到优化方法寻找。从下面的仿真结果可以看到，逼近的性能不仅依赖基函数的选择(参数和结构)，而且还依赖于所使用的学习算法[15]。

被逼近的函数为如下多项式：

为了学习这个被逼近的函数，使用区间[-4，4]内的随机样本函数来产生200个输入输出数据作为训练集。预先确定的参数如下，且跟文献[7]和文献[12]所选一样：

dmax=2，dmin=0.2，γ=0.977，β=0.9，σ0=2，

emax=1.1，emin=0.02，k=1.1，kerr=0.001 5

仿真结果如图2所示。表3列出了用均方根误差估计的结构和性能方面的对比。

如图2(a)所示，经过54个训练数据，规则数保持稳定。从图2(b)来看训练时的实际输出误差很快达到稳定，图2(c)均方根误差(RMSE)保持稳定，图2(d) 实现了非线性函数(+)与它的逼近(o)。

图2 非线性函数逼近Fig.2 nonlinear function approximation

D-FNNOLS[14]M-RANRANEKF模糊规则数67813可调参数数量24222540训练次数2007200200均方根误差0.005 20.008 00.043 60.026 0

表4 RBF单元的分布Table 4 Distribution of RBF elements

由图2(d)及表4可以看出，由D-FNN产生的规则分布在输出变化大的地方，并根据变化的大小和快慢，以不同的高斯宽度来实现，从而使得可容纳的局部域达到最大。与之不同，OLS方法中，每个RBF的宽度是固定的，当被逼近的函数在不同点出现缓慢不同变化时，基函数的自适应性就差，在变化剧烈的地方，可能会要求有多个RBF产生。如本例中，由OLS产生的RBF节点就有两个非常接近的，即C1=-1.022 8及C3=-1.019 2。所选高斯宽度越小，这个问题越突出。同时，也可以看到，OLS方法确定的规则在整个输入变量空间中并不是均匀分布的，所以，所需规则数多，即使如此，精度还是不如D-FNN高。

3 结 论

在D-FNN中采用了修剪策略，可以检测到不活跃的模糊规则并加以剔除，从而可获得更为紧凑的结构。在D-FNN中前提参数(高斯宽度)是在学习过程中自适应地进行调整。D-FNN线性参数在每一步由TLS或者KF方法决定的，而不像RAN、RANEKF及M-RAN是由预测误差确定的。因此，这些最优参数可以在学习的过程中立即得到。用这种方法得到的解是全局最优的，因此，只需一步训练就可以达到目标而不需要迭代学习。采用分级学习的思想能保证更简洁的结构和更短的学习时间。仿真结果表明，D-FNN具有以下明显的优点：快速的学习速度、紧凑的系统结构、强大的泛化能力。