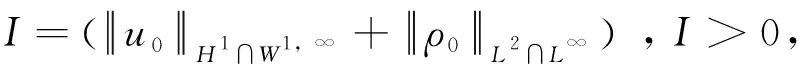两个分支的Degasperis-Procesi系统的弱适定性∗
陈丽娜,关春霞, 冯兆永,刘成霞
(1. 广东工业大学应用数学学院,广东 广州 510520;2. 中山大学数学学院,广东 广州 510275;3. 南方医科大学口腔医院,广东 广州 510280)
关于Degasperis-Procesi(DP)方程的研究目前已有较多的研究成果[1-10],本文主要研究两个分支的DP系统:

(1)


(2)
如果ρ=0,则系统(2)为文献[11]中的DP方程。DP方程具有双哈密顿函数和尖峰孤立子解,完全可积[12],是非线性水波动力学的一个模型[13]。Escher等[14]研究了DP方程解的爆破率和弱解的整体存在唯一性。
本文运用特征线方法将DP系统化成ODE系统,首先证明该ODE系统解的存在唯一性,再证明原系统在(H1(R)∩W1,∞(R))×(L2(R)∩L∞(R))中解的存在唯一性并给出解对初值的弱连续依赖性结论。
注1 在本文中,为方便起见,H1(R),W1,∞(R),L2(R),L∞(R)空间中的R均省略。
1 ODE系统解的存在唯一性
对Cauchy 问题(2)的光滑解(u,ρ),定义x(β,t)为系统(2)的特征线,β为初值,有
(3)
对任意I>0,由常微分理论知方程(3)有唯一解x∈C1([-I,I];R),定义

M(β,t)=
(1+ζβ(δ,t))dδ
(4)
令
N(β,t)=∂xM(β,t)=
(5)

类似地,可以求出T,U关于t求导的等式,得到如下ODE系统
(6)
其中M,N的定义见式(4)-(5)。
定义空间X=H1∩W1,∞,Y=L2∩L∞,我们证明系统(6)在空间X×X×Y×Y中存在唯一解。
为证明ODE系统的存在唯一性给出如下定义和命题:
定义1 对任意α>-1,给定Oα={ζ∈X:essinfζβ≥α}∩X,设x(β,t)=ζ(β,t)+β,其中ζ∈Oα,有xβ=1+ζβ≥1+α>0;由文献[15]知:当β∈R时映射β→x(β)是同胚的,存在可逆函数记为ψ,定义
n(·)=(ζ(·),U(·),T(·),S(·))∈
Oα×X×Y×Y;
利用变量替换和卷积公式以及式(5)-(6)可得
M(n)(β)=
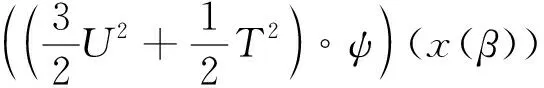
(7)
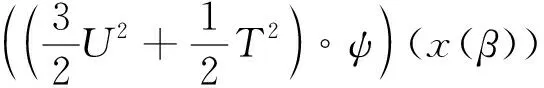
(8)
系统(6)看成抽象的ODE系统
命题1 记X1=X×X×Y×Y,X2=Oα×X×Y×Y,则映射F:X2→X1是局部Lipschitz连续的。
证明首先证明F(n)∈X1,

(9)

(10)
(11)
(12)
利用式(9)-(10)得出M(n)∈Y,类似方法可得N(n)∈Y。由式(8)得:
(13)
因而N(n)β∈Y。接着证明F的局部Lipschitz连续。
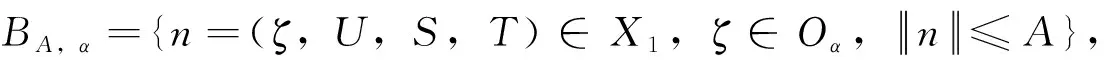
M(ζ1,U,T,S)-M(ζ2,U,T,S)≤

p(x2(β)-x2(δ))·
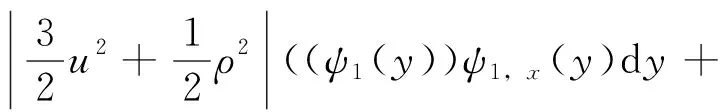
(ζ1(β)-ζ2(β)) +


(14)
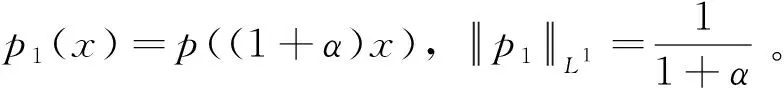
接着证明关于U,S,T的局部Lipschitz连续,利用式(7)有
(15)
结合式(14)-(15)可知
(16)

命题1得证。类似定理3.8[16]的证明过程,可推出以下定理1和命题2成立。

命题2 设n0=(ζ0,U0,S0,T0)∈BA,A>0,则

(17)
存在唯一的一个解满足U0,β=S0(1+ζ0,β),n∈C1([-I,I];BA),并且当I>0时有Uβ=S(1+ζβ)。
综上,ODE系统的存在唯一性证明完成。
2 证明原系统解的存在性和唯一性
接着证明方程(2)在初值z0∈X×Y时解的存在性。
定理2 给定z0=(u0,ρ0)∈X×Y,存在I1>0,对任意I∈(0,I1],方程(2)存在解z=(u,ρ)满足
u∈C0([-I,I];H1)∩
L∞([-I,I];W1,∞)∩C1([-I,I];L2);
ρ∈C0([-I,I];L2)∩
L∞([-I,I];L∞)∩C1([-I,I];H-1)
证明由z0∈(u0,ρ0)∈X×Y,有ζ0=0,U0=u0,S0=u0x,T0=ρ0,n0=(ζ0,U0,S0,T0),可得z0∈BA,利用定理1得存在I1>0,I∈(0,I1],方程(17)存在唯一解n=(ζ,U,T,S)∈C1([-I,I];BA),ζβ>α>-1,定义x(β,t)=β+ζ(β,t),则对任意(β,t)∈R×[-I,I],有x(β,t)>0,所以x(·,t)的逆映射存在,记为ψ(·,t);令
(u(x,t),ρ(x,t))=
(U(ψ(x,t),t),T(ψ(x,t),t)),
(x,t)∈R×[-I,I]
有
(U(β,t),T(β,t))=(u(ψ(x,t),t),ρ(x(β,t),t)),
(β,t)∈R×[-I,I]
同文献[16]有
∂tψ+u∂xψ=0
(18)
Lζ∈C0([-I,I];H1)∩C1([-I,I];L2)
(19)
由U∈L∞([-I,I];W1,∞),T∈L∞([-I,I];W1,∞)以及ψ∈L∞([-I,I];W1,∞),有u∈L∞([-I,I];W1,∞),ρ∈L∞([-I,I];L∞),变量t具有连续性,由于U∈C1([-I,I];X)和X⊂Y,可得Ut∈L∞([-I,I];Y),由文献[16]中的引理2.9,2.10,2.12以及式(18)-(19)有
因为ζ∈C0([-I,I];Y),所以u∈C0([-I,I];Y)。
利用命题2有Uβ=Sxβ,直接计算可得
ux(x,t)=Uβ(ψ(x,t),t)ψx(x,t)=
S(ψ(x,t),t)xβ(ψ(x,t),t)ψx(x,t)=S(ψ(x,t),t)
由S∈C1([-I,I];Y),有St∈L∞([-I,I];Y),对任何t1,t2∈[-I,I],有
(20)
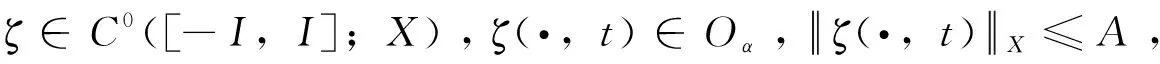
在S(·,t)∈L2以及t1∈[-I,I]条件下,ΡS(·,t1):ζ→S(ψ,t1)是Oα→L2的局部一致连续,即当t2→t1时,有
(21)
结合式(20)-(21)有∂xu∈C([-I,I];L2),u∈C([-I,I];H1)。
因证明ρ∈C([-I,I];L2)跟证明u的正则性相似,所以省略。
利用式(18)和U∈C1([-I,I];X),Uβψx=ux有
-Uβ(ψ(x,t),t)uψx(x,t)+
Ut(ψ(x,t),t)=Ut(ψ(x,t),t)-uux(x,t)
即

(22)
接着证明ut∈C0([-I,I];L2),假设-I≤t1 利用u∈C0([-I,I];H1),ρ∈C0([-I,I];L2),有ut∈C0([-I,I];L2)。 最后证明z=(u,ρ)满足系统(2)的第二个方程:定义 (23) (24) 则qx=ρ,Qβ=Txβ。 利用Uβ=Sxβ,xβ(ψ(x,t),t)ψx(x,t)=1得 Qt(β,t)= (25) (26) 则有 qt(x,t)=Qt(ψ(x,t),t)+ Qβ(ψ(x,t),t)ψt(x,t)=Qt(ψ(x,t),t)+ T(ψ(x,t),t)xβ(ψ(x,t),t)ψt(x,t)= xβ(ψ(x,t),t)u(x,t)ψx(x,t)= -T(ψ(x,t),t)u(x,t)+ (27) 对等式(27)两边同时关于x求导得到: ρt+(uρ)x+uxρ=0 (28) 由u∈C0([-I,I];H1),ρ∈C0([-I,I];L2)可得uρ∈C0([-I,I];L2)。利用式(28)类似可证ρt∈C0([-I,I];H-1),ρ∈C1([-I,I];H-1)结合式(22)、式(28)证明z=(u,ρ)满足方程(2)。 接下来,证明方程(2)解的唯一性。 定理3 假设(u,ρ)满足 u∈C0([-I,I];H1)∩L∞([-I,I];W1,∞)∩ C1([-I,I];L2); ρ∈C0([-I,I];L2)∩L∞([-I,I];L2) 是系统(2)的解,其中(u0,ρ0)∈X×Y,则解(u,ρ)是唯一的。 证明利用文献[16]中(3.22)-(3.23)的相似论证有 u∈C0([-I,I];H1)∩ L∞([-I,I];W1,∞)∩C1([-I,I];L2) 显然方程 ∂tζ(β,t)=u(β+ζ(β,t),t),ζ(β,0)=0 (29) 有唯一解ζ∈C1([-I,I];C0)∩L∞([-I,I];W1,∞),对任意(β,t)∈R×[-I,I]定义: x(β,t)=β+ζ(β,t); U(β,t)=u(x(β,t),t); S(β,t)=ux(x(β,t),t); 利用定理3.10[16],可得essinfxβ= essinfy>ρ> 0以及 (ζ,U,S)(·,t)∈Oρ-1×X×Y,∀t∈[-I,I]; yt=Sy (30) xβ(β,t)=y(β,t) (31) 设T(β,t)=ρ(x(β,t)t),∀(β,t)∈R×[-I,I],利用ζ∈Oρ-1,有T∈L∞([-I,I];Y)。 由于(u,ρ)∈C0([-I,I];H1×L2)是系统(2)的解以及ut∈C0([-I,I];L2)可得 Ut(β,t)=(uux+ut)(x(β,t),t)= -∂xM(β,t)=-N(β,t) (32) ∂βN(β,t)= (33) 即得 (34) 由于式(30)-(31),式(34),xt=ζt=U有 (35) 接着,定义q(x,t),Q(β,t)跟式(23)-(24)中的一样,因而有 (36) 利用Qtβ(β,t)=-ytT(β,t),Qβ=Txβ=Ty有 (37) 结合式(29),(32),(35),(37)有n=(ζ,U,S,T)满足方程(17),利用命题2可得n=(ζ,U,S,T)∈C1([-I,I];X1)和系统(2)的解是唯一的,由于对∀t∈[-I,I],x(·,t)同胚,所以(u,ρ)是唯一的,定理3证明完成。 接下来我们给出解对初值的弱连续依赖性结论。 其中ni=(ui,ρi)为初值u0i(i=1,2)对应的解,Ii(i=1,2)为ni的存在时间,I=minI1,I2。 注2 定理4证明方法类似于定理2的估计过程,这里证明省略。 综合定理1-4得出本文的主要结论: u∈C0([-I,I];H1)∩L∞([-I,I];W1,∞)∩ C1([-I,I];L2); ρ∈C0([-I,I];L2)∩L∞([-I,I];L2) 且 其中常数C>0。此外,在空间(H1∩W1,∞)×(L2∩L∞)中,如果初始值z01→z02,那么存在I>0并且其对应的解z1=(u1,ρ1),z2=(u2,ρ2)满足在空间C([-I,I];H1)∩C1([-I,I];L2)中u1→u2,在空间C([-I,I];L2)中ρ1→ρ2。










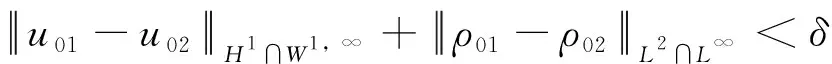
3 结 论