趋于线性标度的增长法：基于局域定域分子轨道的双电子积分

PRICE David R,彭亮,李少鹏,顾凤龙,AOKI Yuriko

(1.环境理论化学教育部重点实验室∥华南师范大学化学与环境学院，广东 广州 510006 ；2.日本九州大学工学院材料科学系，日本 福冈县816-8580；3.日本科学技术厅战略创造研究推进事业(CREST)，日本 埼玉县332-0012)

Modern quantum chemistry can predict the structure and properties of various compounds and elucidate pathways of chemical reactions, but its usefulness is tempered by its poor scaling. The most accurate and consistent methods scale poorly and are limited to small systems even as the performance of computers improves. However, much progress has been made in developing linear scaling methods that can be used to model biological systems. Several methods are currently implemented in GAMESS[1-2]: such as quantum fast multipole moment (QFMM)[3-7], fragmented molecular orbitals (FMO)[8-13], Divide and Conquer (DC)[14-16]and the elongation (ELG) method[17-21].

Li proposed a so-called CIM (Cluster-in-Molecule) method to deal with large systems with localized molecular orbitals, and this method can be extended to MP2 and CCSD levels[22-23]. Another method has been proposed recently as described from fragments to molecule by Liu’s group. Liu’s method also used localized molecular orbitals to divide the whole system into small fragments, and low factor linear scaling can be achieved[24-25].

The elongation method, first proposed by Imamura, Aoki and Maekawa[17]in 1991, has proved to be an effective method to achieving linear scaling for Hartree-Fock[18,26-27]. According to a recent invited perspective[28], elongation computes the Hartree-Fock coefficients for a part of a system then localizes them into frozen and active regions. An attacking group is added to the active region and a new set of Hartree-Fock coefficients is determined which is localized into second frozen region. This process is repeated for the entire system. Originally applied to quasi-one-dimensional systems such as polymers[29], very recently it is generalized to three-dimensional systems such as crystals[30].

Despite elongation’s linear scaling, it only surpasses the performance of conventional QFMM for large systems. To reduce the linear scaling prefactor, a local molecular orbital basis can be used to form the Fock matrix directly rather than through the more time consuming method of forming the Fock matrix in an atomic orbital basis and transforming it to a local molecular basis. What follows is an explanation of the theoretical framework of elongation based on local molecular orbitals, a description of its implementation and the results of test calculations for model systems such as a chain of water molecules.

1 Methodology

To test the efficiency of the new method, a series of calculations were performed for chains of water up to 480 water molecules. The water molecules had bond lengths of 0.96×10-10m and bond angles of 104.5° and were spaced 3×10-10m apart. The number of water molecules assigned to each unit sizes include 3, 4, 5, 6, 8, 10, 12 and 15 for STO-3G, and 4, 5, 6 and 8 for 6-31G. During the regional localization procedure, both the frozen and active regions have one unit.

The efficiency of ELG-HF(LMO) was also tested using a series of polyethylene chains. Bond distance is 1.52×10-10m for carbon-carbon bonds and 1.08×10-10m for carbon-hydrogen bonds, and the bond angle is 109.5° for carbon-carbon-carbon, carbon-carbon-hydrogen and hydrogen-carbon-hydrogen bonds. For the test, units containing of three (N=3), four (N=4), five (N=5) and six (N=6) monomers were used for STO-3G, and three and four monomers were included in each unit for 6-31G.

2 Theory

The basis of Hartree-Fock is the expansion of molecular orbitals,|φi〉, in terms of atomic orbitals,χμ:

(1)

such that the coefficients provide a self-consistent solution to:

FC=SCε

(2)

whereF, the Fock matrix,andS, the overlap matrix, are both in an atomic orbital basis.

Like DC and FMO methods, elongation divides the system into individual units.It begins with a starting cluster; then, adds additional units one at a time as illustrated in Fig.1 until all of the units have been included.A conventional HF calculation determines the molecular orbitals of the starting cluster.These orbitals are localized by region and assigned to either active-those that will interact with the next unit-and frozen-those that only react weakly with the next unit.The next unit is added and only the molecular orbitals of the active region are determined.The current active region is localized into the next frozen and active region and the process is repeated until all the units have been added.

Fig.1 Schematic illustration of the elongation method

Only the coefficients for the active region are altered. It transforms the Fock matrix from an atomic orbital basis to a regional localized basis:

(3)

before determining a set of orthonormal coefficients that satisfy:

(4)

In elongation, the density and Fock matrices are separated into two parts: orbitals in the frozen region (A) and orbitals in the active region (BMwhereBis from the active region previous elongation step andMis the attacking unit for the current step). For the density matrix, the summation over occupied molecular orbitals is divided into two parts:

(5)

and

(6)

such that

(7)

As a result, the Fock matrix becomes:

(8)

(9)

where

(10)

and

(11)

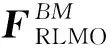
Fig.2 Schematic comparing AO ELG-HF and LMO ELG-HF with conventional HF

3 Transformation of two electron integrals

Ordinarily, the transformation of two electron repulsion integrals scales asO(N5) meaning that post Hartree-Fock methods that utilized molecular orbitals are generally at leastO(N5) scaling. However, for regional localized molecular orbitals, this transformation constant scaling is achieved.

(12)

First, only molecular orbitals in the active region are transformed, and the number of RLMO two electron integrals can remain more or less the same for each elongation step and stored in memory as opposed to written to disk. Second, only a fixed number of atomic orbitals contribute to the integrals for each step. Generally, most programs group integrals by atomic orbital shells rather than individual atomic orbitals (AO). To identify the shells needed in the calculation, the overlap of each atomic orbital shell is determined as follows:

(13)

and

(14)

If the overlap is below a certain threshold(δC), then the shell may be excluded from the transformation. As a result, the number of atomic orbitals needed in the transformation is roughly constant (NCUT) for each elongation step and is also a feature of AO based ELG-HF. The transformation becomes:

(15)

In this form, the transformation divides into four partial transformations:

(16)

(17)

(18)

and

(19)

Although the use of cutoff based on the overlap of atomic shells with the active region provides linear scaling, the method requires more computer time than conventional HF even for relatively small active regions. To be a useful alternative to conventional HF, additional methods of prescreening of the AO integrals and LMO coefficients are needed to reduce the time required for the transformation.

First, reducing the number of AO integrals computed reduces the time needed for the transformation. Commonly, using the Cauchy-Schwarz inequality:

(20)

reduces the number of AO integrals fromO(N4) toO(N2) as the system size becomes larger. IfTμvTρσ<δs, the AO integral is negligible and not computed for the transformation.

Second, the maximum coefficient product used for local correlation methods such as LMP2[33-34].

(21)

(22)

then the first and second partial transformations can be neglected.

Third, the second, third and fourth partial transformations can be computed as scalar products of the coefficientsCρr,Cvq,Cμp, and a vector containing N or more elements ((μυ|ρs),(μυ|rs), etc.). If |Cpr|<δ,Cpr(μυ|ρs) has a negligible effect on the summation in the second transformation and can be neglected for alls. If |Cvp|<δ, it can be neglected for allr,s, andq; while if|Cμp|<δ, allrandscan be neglected.

Fourth, the molecular orbitals are prescreened. The Cauchy-Schwarz inequality:

(23)

provides the basis for the prescreening. Rather than compute (pq|pq)directly, it will be estimated from the molecular orbital’s (p) population on each atom (α):

(24)

(25)

then is small and can be excluded for all molecular orbitalsrands.

4 Localized initial guess

One bottle neck for performance for larger active regions and bonded systems is the delocalized initial guess. A delocalized guess that provides to faster converge in AO based ELG-HF is poorly suited for active regions with a large number of molecular orbitals. An ideal starting guess only need a few atomic orbitals for each molecular orbital and would be mostly zero to optimize cutoff and other prescreening. One approach would be to localize the initial guess molecular orbitals using a conventional localization technique such as Boys[35],Pipek-Mezey[36]or Edmiston-Ruedenberg[37].Both Pipek-Mezey and Edmiston-Ruedenberg localizations require significant amounts of CPU time and Boys increased the number of integrals over the threshold by 20% to 26% and decreased the performance by 7% to 9% for polyethylene chains.

Alternatively, an initial guess for the molecular orbitals can be constructed from hybridized orbitals. First, the valence orbital of each atom is assigned an orbital hybridization (s, sp, sp2, sp3, etc.) estimated from its geometry which is represented by a linear combination of the atomic orbitals. Then, these hybridized atomic orbitals are used to construct bonding and anti-bonding molecular orbitals. Any additional atomic orbitals are added to the virtual space. Orbitals are constructed based on the current geometry. If a geometry changes the hybridization, the procedure will adjust the molecular orbital accordingly. The resulting molecular orbitals for the active region are orthonormalized with the frozen region to provide an orthonormal set of molecular orbitals. At present, this initial guess is implemented for STO-3G and 6-31G basis sets.

5 Results

5.1 Thresholds for the Schwarz inequality, coefficient prescreening and molecular orbital prescreening

The absolute average difference in energy relative to a threshold of 10-12for both the Schwarz inequality and prescreening is shown in Table 1. Two trends from Table 1 can be found: one, the higher threshold of the two thresholds leads to the deviation from the reference energy, and two, the order of magnitude of this deviation is two orders of magnitude higher than the energy threshold. Finally, the deviation is systematic: it did not depend on the unit size and remained roughly the same for each elongation step.

To determine the ideal thresholds for accuracy (Tables 1 and 2), the overall difference between ELG-HF and conventional HF is between 10-6and 10-5depending on the size of the system. Therefore, both the Schwarz inequality and threshold for the coefficient prescreening thresholds ought to be set at either 10-9or 10-8to avoid affecting the total energy.

Once the ideal threshold for the Schwarz inequality and coefficient prescreen were obtained, a series of similar calculations using water chains with 120 H2O molecules and H—(CH2CH2)20—H were run to determine the ideal threshold for molecular orbital prescreening. As shown in Table 3, minimum threshold of 10-10is needed to maintain the same accuracy as ELG-HF(AO).

polyethylene (H—(CH2CH2)20—H) and 120 water molecule chain using ELG-HF(LMO) with STO-3G and 6-31G basis sets.

Differences are relative to calculation with thresholds of 10-12

5.2 Water molecule chain

The energy difference between ELG-HF(LMO) and conventional QFMM included in Table 4 depends on the cluster size and the thresholds used for the Schwarz inequality and coefficient prescreening. For smaller clusters the energy difference per atom is low, and improves as the cluster size increases. However, the thresholds need to be lowered to improve the accuracy once the energy difference reaches 10-7a.u.

Table 2 Comparison of energy differences (a.u.) of the system for water chains of length n relative to conventional HF. For

ELG-HF(LMO), five (N=5) and ten (N=10) water molecules are included in each unit. For ELG-HF(AO) twenty (N=20) water molecules are included in each unit. During the regional localization procedure, both the frozen and active regions have one unit

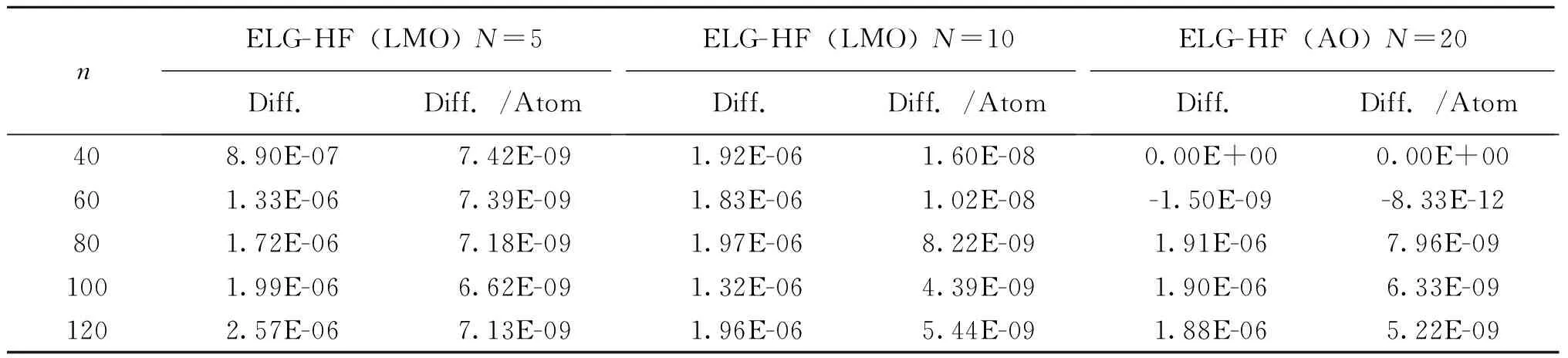
nELG-HF(LMO) N=5Diff.Diff./AtomELG-HF(LMO) N=10Diff.Diff./AtomELG-HF(AO) N=20Diff.Diff./Atom408.90E-077.42E-091.92E-061.60E-080.00E+000.00E+00601.33E-067.39E-091.83E-061.02E-08-1.50E-09-8.33E-12801.72E-067.18E-091.97E-068.22E-091.91E-067.96E-091001.99E-066.62E-091.32E-064.39E-091.90E-066.33E-091202.57E-067.13E-091.96E-065.44E-091.88E-065.22E-09

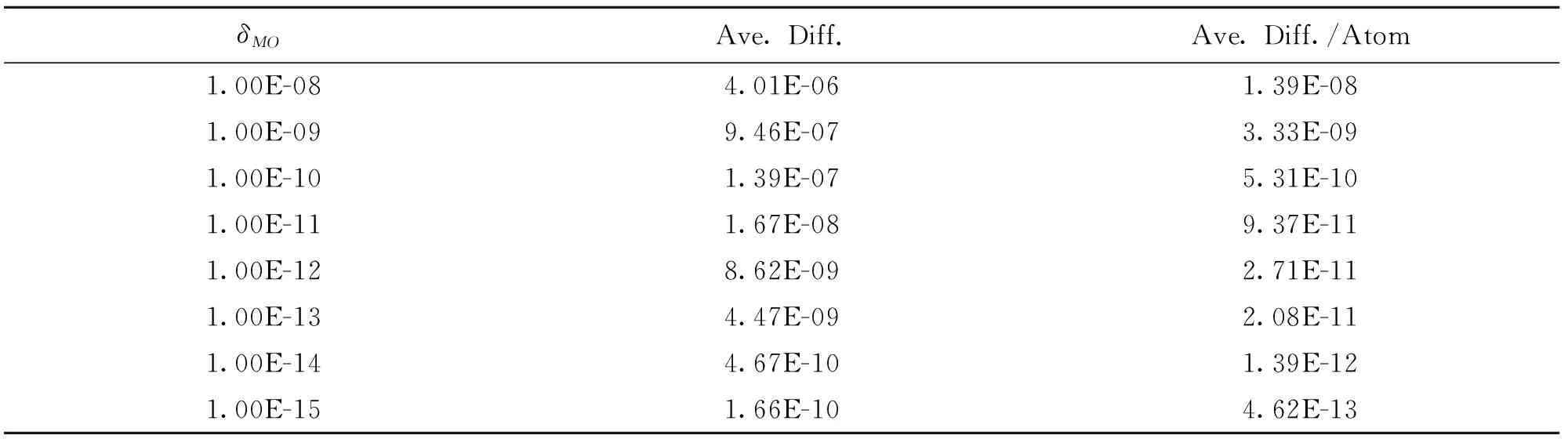
Table 3 Effect of threshold for molecular orbital prescreening on relative energy difference. Absolute average of polyethylene and water chain

Table 4 Comparison of total energy for various cluster sizes to conventional QFMM. N is the number of water molecules in each unit. During the regional localization procedure, both the frozen and active regions have one unit

1)Conventional HF energy -8 995.764 196 a.u.;2) Conventional HF energy -9 118.520 933 a.u.

The time required for the calculation scales linearly as is shown in Fig.3 and Fig.4.Note, the CPU times in Fig.3 and Fig.4 have been adjusted to reflect using the cutoff technique for the AO Fock matrix. Two sets of ELG-HF(LMO) calculations were performed. One included the cutoff atomic orbitals in the AO Fock matrix for each elongation step, the other excluded them. The total CPU time was then adjusted to include how much time would have been used if the cutoff atomic orbitals were included in the AO Fock matrix for the final elongation step. The net result is a factor of four less CPU time for ELG-HF(LMO) compared to conventional HF as shown in Fig.4 even with linear scaling methods such as QFMM. But, the number of molecular orbitals in the active region determines the usefulness of the transformation. Smaller basis sets such as STO-3G and smaller clusters sizes provide the fastest transformations as Fig.3 shows, but other parts of the calculation become more significant (one electron integrals and the AO Fock matrix for the frozen region) as the calculation proceeds. It shows that for a smaller unit size, five water molecules, ELG-HF(LMO) is always faster than conventional for STO-3G. Even a large unit size, ten water molecules, is faster than ELG-HF(AO). The slope of the line for ELG-HF(LMO) is smaller than ELG-HF(AO) forN=4, but larger forN=6 and suggest that this method may be limited to small active regions.

Using cutoff proved to be the most significant contributor to linear scaling. First, it identified the shells that would be significant in the transformation and limited the number of comparisons that would be needed. Without cutoff, the Schwarz inequality, coefficient prescreening and indexed arrays still identify which integrals would be needed for the transformation, but it also increased the number of comparisons needed significantly especially for larger basis sets like 6-31G. A factor of 3.7 to 58.9 more Schwarz comparisons added 1 to 20 seconds more CPU time to the first partial transformation and more than 20% to the total CPU time for a 120 water molecule chain. The transformation no longer uses a roughly constant amount of time and linear scaling is lost (See Fig.5). This effect would have been greater if maximum Schwarz inequality was also excluded.

Fig.3 Effect of unit size on CPU time for ELG-HF(LMO)/STO-3G. Each unit has N water molecules and during the regional localization procedure, both the frozen and active regions have one unit. Conventional HF uses linear scaling methods to form the density and Fock matrices. Calculations were run on Dell T5500 Precision Workstations using one 3.06 GHz Xeon X5567 CPU

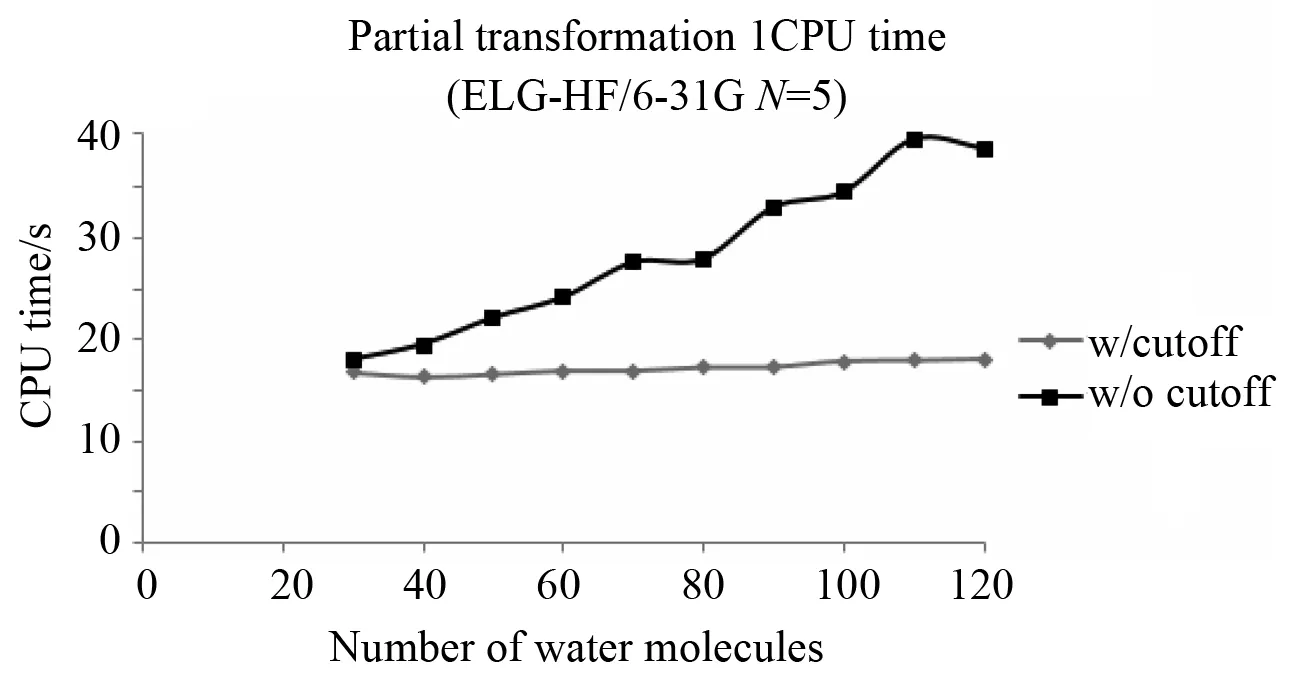
Fig.4 Comparison of ELG-HF(LMO)/6-31G with Conventional HF/6-31G. Each unit of ELG-HF(LMO) has five water molecules and during the regional localization procedure, both the frozen and active regions have one unit. Conventional HF uses linear scaling methods to form the density and Fock matrices, but solving the HF equations does not scale linearly with system size. Calculations were run on Dell PowerEdge R910 Server using one 2.26 GHz Xeon X7560 CPU

The maximum Schwarz inequality and Schwarz inequality also had a significant effect on the amount of time needed for the two electron integral transformation as illustrated in Table 5. The number of integrals computed dropped by a factor of 27.9 for STO-3G (N=10), 38.4 for 6-31G (N= 10) and 63.9 STO-3G (N= 20). The total CPU time for a 120 water molecule chain was reduced by a factor of between 11.5 and 14.6.

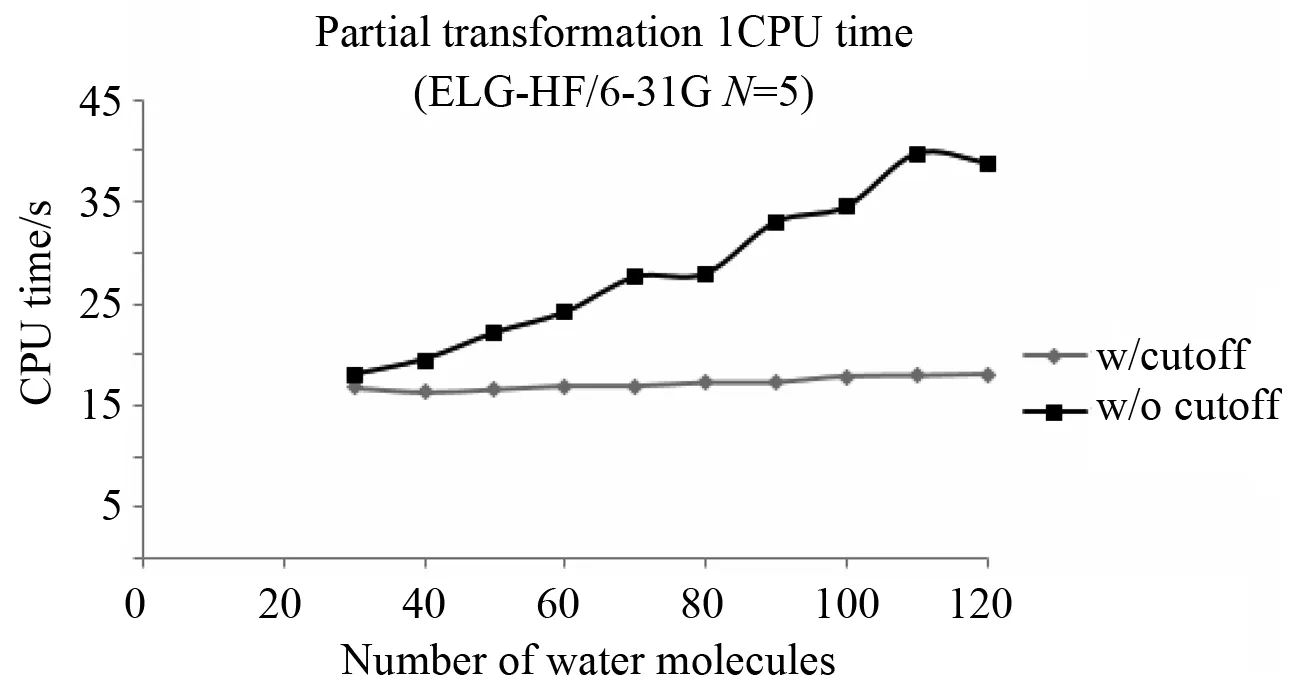
Fig.5 Effect of cutoff: Comparison of the CPU time for the first partial transformation for each elongation step with and without cutoff using 6-31G basis set. Calculations were run on Dell T5500 Precision Workstations using one 3.06 GHz Xeon X5567 CPU

The coefficient prescreening had a modest effect (Table 5) since only 50% to 60% of the coefficients are below the default threshold of 10-9. The CPU time’s average ratio of including prescreening to excluding prescreening range from 0.59 to 0.74 for the second, third and fourth partial transformations.Coefficient prescreening did reduce the total CPU time more as the size of the active region increased, but doubling the size of the active region fromN=10 toN=20 for STO-3G still required an average factor of 8.7 more CPU time. Excluding coefficient prescreening required an average factor of 10 more CPU time when the system size double for STO-3G.

Localizing the molecular orbitals (whether using Boys localization or the hybridized orbitals described earlier) also allow them to be prescreened and reduces the amount of memory needed for the two electron integrals. The number of molecular orbital pairs (p,q) grows linearly with system size and allows the number of two electron integrals to grow quadratically. As a result, less than 2% of the LMO integrals are needed for larger active regions (See Fig.6). Correspondingly,it also reduces the relative time needed for the transformation as is shown in Table 5 and the total time needed for the calculation as is shown in Fig.7. Though the set of hybridized molecular orbitals provide a greater reduction in CPU time compared to molecular orbital prescreening.

Fig.6 Effect of molecular orbital prescreening of 120 water molecule chain with STO-3G basis set. The number of molecular orbital pairs included using Equation 25 is indicated by Pairs Inc. The number of two electron integrals in RLMO basis computed when prescreening is used is indicated by Int. Inc. Pairs Tot. and Int. Tot. are the total number of pairs and integrals if no molecular orbital prescreening is used.

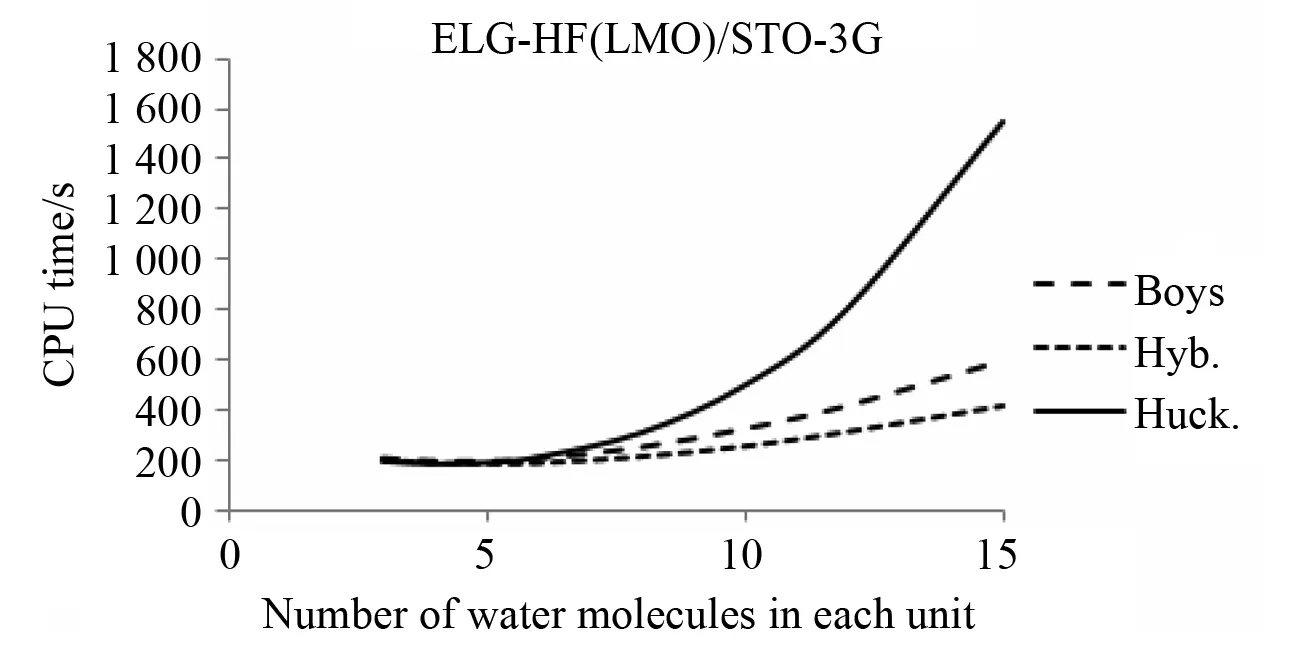
Fig.7 Effect of unit size on total CPU time in a 120 water molecule chain with STO-3G basis set. Calculations were run on Dell PowerEdge R910 Server using one 2.26 GHz Xeon X7560 CPU.Huck means a standard initial guess from Hückel theory. Boys corresponds to localizing the standard initial guess using Boys localization procedure. Hyb. corresponds to forming an initial guess from hybridized orbitals as described in the text.

Schwarz inequalityMaximum Schwarz inequalityCoefficient prescreeningMolecular orbital prescreeningHybrid. initial guessSTO-3G (N=10) 1)0.0870.5270.8051.0000.886STO-3G (N=20) 1)0.0680.4020.6980.8850.4366-31G (N=10) 1)0.0790.4330.7510.9680.636

1)Nis the number of units in each cluster.

To reduce the time required for each elongation step further, the cutoff technique typically used to form the AO Fock matrix in ELG-HF(AO) is also used here. This effect accounts for one fifth of the total CPU time of the calculation and it is only needed to compute the total energy of the system which may be done during the final elongation step.

5.3 Polyethylene

As in the previous case of water chains, the energy difference depends on the size of the active region and the distance the attaching monomer is from the starting cluster, but at least five monomers are needed between the frozen region and attaching unit to achieve an accuracy of 10-8a.u. per atom. However, the overall efficiency was poor. Four monomers in each unit took 62% more CPU time than conventional QFMM but had a large energy difference (0.000 16 a.u.) while a unit size of six monomers took nearly three times longer than conventional. The primary reason for this inefficiency: cutoff had less of an effect for polyethylene chains than for the water chains in the previous test. Only 66 of 480 AO shells were needed for a chain of 120 water molecules with six molecules in each cluster while 99 of 482 were needed for H—(CH2CH2)60—H, and H—(CH2CH2)60—H more than twice as many coefficients above the standard threshold than a similar sized chain of water molecules.Also, the coefficient prescreening only excluded between 26.5% and 28.7% of the coefficients compared to 50% to 64% for water chains. The result is the transformation takes on average 29.0 s for polyethylene once cutoff begins compared to 4.0 s a water chain, and the total time for the calculation takes on average 997.5 s for H—(CH2CH2)60—H compared to 201.8 s for a similar sized chain of water molecules. To correct this inefficiency, a more localized starting guess is needed for bonded systems.

6 Conclusions

Using LMO based two-electron integrals for elongation provides linear scaling and the techniques included reduce the CPU time to varying degrees. It is most effective if either the number of molecular orbitals in the starting cluster is small or the initial guess is well localized. A more localized initial guess is also needed to effectively prescreen small LMO two-electron integrals to reduce both the CPU time and the amount of memory needed for storing the two electron integrals. Also, one remaining computational bottleneck is forming the Fock matrix for the entire system which is still required to compute the energy of the frozen region. Even if a proven linear scaling technique such as QFMM is used, the effect on elongation is quadratic scaling which can undermine any gain from using LMO two electron integrals.