结构面刚度对岩体弹性纵波传播特性影响的数值模拟
黄真萍,曾焕接,曹洋兵,陈俊熙
(1.福州大学环境与资源学院; 地质工程福建省高校工程研究中心,福建 福州 350108; 2.国土资源部丘陵山地地质灾害防治重点实验室,福建 福州 350108)
0 引言
岩体中存在大量性质不同、规模各异的结构面,弹性波传到这些结构面时,将发生反射、透射现象,并由此导致能量、振幅、波速等发生变化.鉴于弹性波在岩体中的传播特性问题涉及岩体工程爆破、声波检测及微震监测等领域,众多研究人员对此开展大量卓有成效的研究,取得重要进展.
起初,研究人员将岩体看作连续、均匀、各向同性的介质,采用等效连续介质力学方法研究弹性波传播问题.考虑到这种模型过于简化,与实际情况差距甚大,因此位移不连续模型[1-4]被提出,此模型认为弹性应力波穿过节理面时,应力场是连续的,而位移是不连续的,从而较好地模拟应力波在节理岩体中的传播特性及过程.除此之外,结构面对于岩体弹性波传播的振幅衰减、高频滤波及信号延迟等效应[4-8]也被实验揭示,研究人员基于试验结果开展相关的理论建模及力学描述研究.
由于室内试验及解析计算等研究手段的局限性,研究人员尝试利用离散元程序进行结构面对岩体弹性波传播特性影响的研究[9-15],离散元模拟方法逐渐成为一种重要的研究方法.茹忠亮等[9]得出节理面越粗糙,法向刚度越小,弹性波衰减程度越大,弹性波的波速降低越快.卢文波[10]指出节理刚度越大,其透射系数也越大; 石崇等[11]认为节理面法向(或切向)刚度越大,各点透射率越高; Myer等[1]发现节理刚度越大,透射波形越接近于入射波,刚度越小,透射波波幅减小、高频滤波.王卫华等[12-13]发现节理面粗糙度相同时,透射系数随法向刚度的增大而增大.陈勇等[14]认为一维应力波垂直节理传播时,随着节理法向刚度的增大,反射波波幅减小、频率降低,透射波的波幅增大、频率降低.
综上可知,目前的研究集中在岩体结构面对应力波的透射系数、反射系数的影响及波的振幅衰减、高频滤波、信号延迟等方面,而关于岩体结构面法向刚度、切向刚度如何定量影响岩体弹性纵波波速及初至纵波振幅等问题则鲜有研究报道.本文基于3DEC离散元分析平台,通过连续介质模型检验软件及自编程序的准确性,基于单裂隙岩体模型,定量研究结构面法向刚度、切向刚度对岩体弹性纵波传播特性的影响规律,从而为相关岩体工程动力响应、安全性评价及数值模拟参数设置等提供理论支撑.
1 3DEC软件及自编程序的可靠性
基于3DEC软件和FISH语言,自编可精确监测模型边界动力响应的离散元计算程序,研究裂隙岩体弹性纵波传播特性.以等效连续介质模型的解析解作为标准参考值,检验3DEC软件的适用性及自编程序的准确性.

图1 岩块数值模型Fig.1 Numerical model of rock block
对于连续、均匀、各向同性的弹性材料,其弹性纵波传播速度Cp的理论解如下:
(1)
式中:ρ为材料的密度;E为材料的杨氏模量;μ为材料的泊松比.
1.1 数值模拟概况
构建1 m×1 m×10 m的长方体模型如图1所示,将模型的顶面及四个立面设为自由边界条件(由于底面施加纵波,侧面的自由边界条件不会有反射和折射,能达到粘性边界条件的目的),在模型底面施加速度型正弦纵波如下式 .
vz=Asin(ωt)
(2)
式中:vz为底面z方向的速度(m·s-1);A为振幅,本次取0.1 m·s-1;ω为角频率,本次取200 π,即频率f为100 Hz.

表1 岩块物理力学参数
根据岩体动力响应特征,选择瑞利阻尼模型,设置最小临界阻尼比为0.05、最小临界中心频率为100 Hz,设置的岩块物理力学参数如表1所示.在模拟弹性波传播时,网格单元的尺寸对计算结果的准确性有很大影响,网格尺寸过大容易导致波形失真及波峰、波谷的位置偏离真实值,进而导致波速计算值误差过大.钱七虎院士[15]建议,网格尺寸与波长之比不应大于1/10~1/8.根据以上设置及式(1),该岩块的纵波速度理论解为3 651 m·s-1,故输入波的波长为36.51 m,由此设置网格尺寸为0.5 m,可以较精确地模拟波在模型中的传播.
1.2 可靠性论证
经计算发现,同样的程序每次计算的结果都有轻微差别,这可能是数值截断误差等导致的离散性.经过大量的计算尝试,发现取6次数值计算值的平均值作为最终计算结果是稳定、可靠的.因此,本文中所有列出的数值模拟结果数据都是取6次数值计算结果的平均值.

图2 纵波波速理论值与模拟值随杨氏模量E的变化 Fig.2 Theoretic calculations and numerical simulation results of P-wave velocity as a functionof the Young's modulus E
按照表1的参数设置,保持泊松比μ、密度ρ不变,依次改变杨氏模量E,得出的数值计算结果与理论解对比情况见图2.由图可知,数值模拟值与理论值相当接近,两者随杨氏模量E变化的曲线也相当吻合.同样地,分别改变泊松比μ和密度ρ进行数值模拟,结果也显示弹性纵波波速理论值与模拟值较为接近,两者的相对误差皆小于2%.从而证实了程序的可行性和可靠性,并间接证明了上述数值模型尺寸、网格尺寸等程序设置的合理性,可应用于后续结构面岩体研究.
2 结构面刚度影响的数值模拟
基于上述被论证为合理、可靠的3DEC数值模型及自编程序,为研究结构面刚度对岩体弹性纵波传播特性的影响,在连续介质模型中部施加一条水平光滑的结构面(为接触面单元),如图3所示.岩块的物理力学参数、边界条件、阻尼模型及参数、网格尺寸等设置情况与上节相同.
图3 单结构面岩体数值模型 Fig.3 Numerical model of rock mass
2.1 研究方案
结构面刚度是反映结构面几何构成的函数,与结构面的风化蚀变特征、张开度、粗糙度及其吻合情况等有关.因此,平直结构面和结构面刚度可等效模拟复杂天然结构面.
为研究岩体结构面法向刚度、切向刚度对弹性波传播特性的影响,需要首先确定法向刚度、切向刚度的合理取值范围.需要说明的是,3DEC软件中结构面刚度的基本单位为Pa·m-1,并非N·m-1.由结构面的泊松效应可知,结构面法向刚度与切向刚度的比值应为[1,10].一般来说,对于离散元计算,法向刚度和切向刚度应小于与该节理邻接块体的等效刚度的10倍,公式如下:
(3)
式中:K为块体的体积模量;G为块体的剪切模量; Δzmin为与该节理邻接块体的最小棱边长度.此要求一般仅为提高数值计算效率,对本文的简单模型而言,结构面刚度超出此范围不会显著增加计算复杂度,反而能核实相关规定的正确性.
根据数值模拟基本情况,确定出的结构面法向刚度总体取值范围为7.5~7.5×106MPa·m-1,切向刚度总体取值范围为3.0~3.0×106MPa·m-1,并通过以下基本思路研究结构面刚度对岩体弹性纵波传播特性的影响:
1) 保持结构面切向刚度ks不变,将kn/ks由1逐渐增加至10.
2) 保持结构面法向刚度kn不变,将kn/ks由1逐渐增加至10.
3) 保持结构面法向刚度与切向刚度之比为2.5不变,同时改变法向刚度与切向刚度的大小.
2.2 数值模拟结果分析
2.2.1 结构面法向刚度的影响分析
固定结构面切向刚度为最低级(3 GPa·m-1),将kn/ks由1逐渐增加至10,即逐渐增大结构面法向刚度的大小; 再将结构面切向刚度调至下一级,逐渐增加法向刚度; 最终将结构面切向刚度调至最高级(30 GPa·m-1),并同样地逐渐增加法向刚度.从而在大跨度的切向刚度ks、法向刚度kn与切向刚度ks之比kn/ks范围内,研究法向刚度对弹性纵波传播特性的影响.
不同级的切向刚度、不同kn/ks比值条件下,初至纵波振幅随法向刚度kn的变化如图4(a)所示,纵波波速随法向刚度kn的变化如图4(b)所示.给定激发纵波的振幅为100 mm·s-1,若无此结构面,岩块的弹性纵波波速理论值为3 651 m·s-1.

图4 不同切向刚度下初至纵波振幅和纵波波速随kn/ks的变化Fig.4 Amplitude of first break and P-wave velocity as a function of kn/ks at variousdiscontinuity tangential stiffness
由图4(a)可知,当切向刚度不变时,初至纵波振幅随kn/ks比值的增加而增大,即初至纵波振幅随法向刚度的增加而增大,但增长速率逐渐减小,最终初至纵波振幅趋近于激发纵波振幅; 当切向刚度固定为3~12 GPa·m-1时,初至纵波振幅在kn/ks比值为1~3.5之间为陡增段,且切向刚度越小,增长速率越大,在kn/ks比值大于3.5后为缓增段,增长速率逐渐减小; 当切向刚度固定为12~30 GPa·m-1时,初至纵波振幅在kn/ks比值为1~10之间皆为缓增段,增长速率逐渐减小.
由图4(b)可知,当切向刚度不变时,弹性纵波波速随kn/ks比值的增加而增大,即弹性纵波波速随结构面法向刚度的增加而增大,但增长速率逐渐减小,最后趋于稳定,最终稳定值介于3 566~3 670 m·s-1之间,与连续介质弹性纵波波速理论值基本相当.
2.2.2 结构面切向刚度的影响分析
由上节可知,初至纵波振幅和纵波波速与结构面法向刚度密切相关,但无法判定其与结构面切向刚度有关.为此,在本节中,固定结构面法向刚度为最低级(1.5 GPa·m-1),将kn/ks比值由1逐渐增加至10,即逐渐减小结构面切向刚度的大小; 再将结构面法向刚度调至下一级,逐渐减小切向刚度; 最终将结构面法向刚度调至最高级(30 GPa·m-1),并同样地逐渐减小切向刚度.从而在大跨度的法向刚度kn、法向刚度kn与切向刚度ks之比kn/ks范围内,研究切向刚度对岩体弹性纵波传播特性的影响.
不同级的法向刚度条件下,初至纵波振幅随kn/ks比值的变化如图5(a)所示,纵波波速随kn/ks比值的变化如图5(b)所示.
由图5可知,当法向刚度不变时,初至纵波振幅和纵波波速随kn/ks的增加都几乎不变(曲线上局部微小的波动是由于数值误差引起).由此表明,结构面切向刚度对岩体初至纵波振幅和纵波波速几乎没有影响.
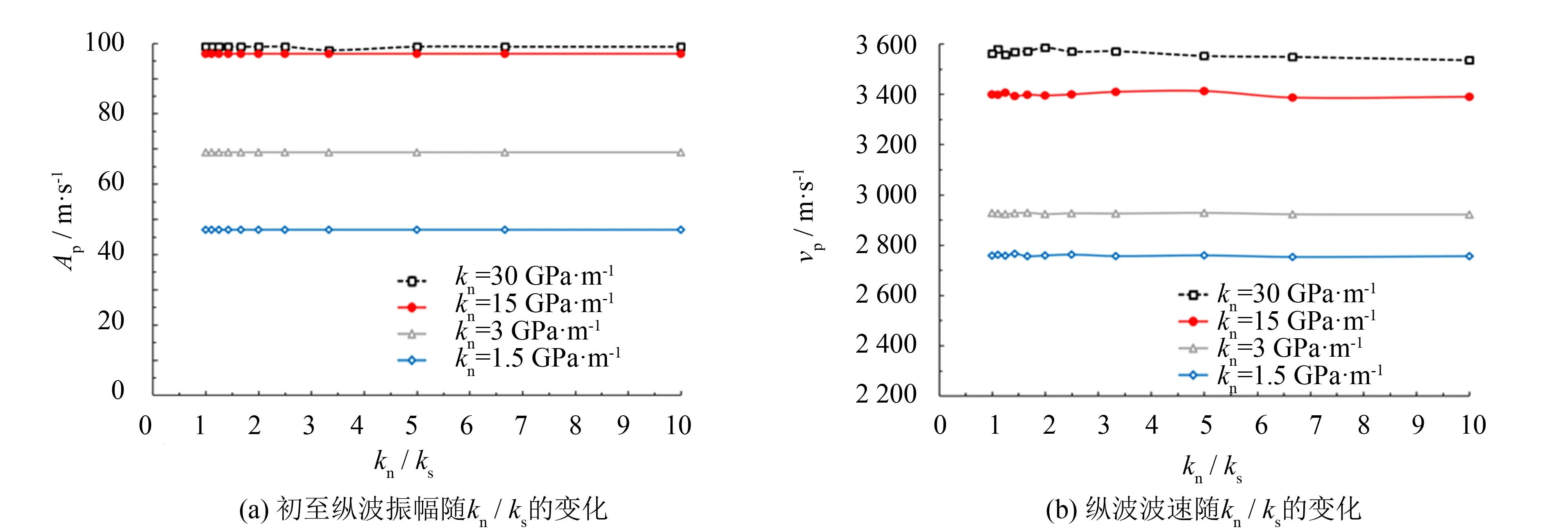
图5 不同法向刚度下初至纵波振幅和纵波波速随kn/ks的变化Fig.5 Amplitude of first break and P-wave velocity as a function of kn/ks at variousdiscontinuity normal stiffness
2.2.3 考虑结构面间距和岩块杨氏模量的结构面刚度的影响分析
由上两节可知,结构面法向刚度对岩体纵波传播特性有重要作用,而切向刚度对纵波传播几乎没有影响.但是,上述研究以岩块纵波波速为基准值,仅孤立地研究法向刚度绝对值的影响规律,忽视了结构面法向刚度与岩块杨氏模量之间的紧密关联,因而难以将岩体弹性纵波传播特性进行整体考量.并且,岩体中的结构面数量庞大,仅一条结构面无法反映工程岩体实际情况.为此,引入比值E/(S·kn),用以衡量岩块杨氏模量E(本文设置为30 GPa)、结构面间距S(对于本文的单结构面岩体模型,S为岩体模型高度,即10 m)和结构面法向刚度kn的组合关系对岩体弹性纵波传播特性的综合影响,从而使得研究结论具有更好的普适性.
结构面法向刚度kn与切向刚度ks之比为2.5时,是硬岩工程的常见工况,故本次保持kn/ks比值为2.5不变,同时改变结构面法向刚度kn与切向刚度ks的大小,研究E/(S·kn)对岩体弹性纵波传播特性的影响.初至纵波振幅Ap/激发纵波振幅A0随E/(S·kn)的变化如图6(a)所示,纵波波速vp/连续介质纵波波速理论值Cp随E/(S·kn)的变化如图6(b)所示.

图6 Ap/A0和vp/Cp随E/(S·kn)的变化Fig.6 Ap/A0 and vp/Cp as a function of E/(S·kn)
1) 由图6(a)可知,初至纵波振幅Ap/激发纵波振幅A0随E/(S·kn)的增大而减小,具体的减小规律为: ① 当E/(S·kn)≤0.1时,初至纵波振幅衰减速率极小,衰减幅度不超过2%,Ap/A0接近于1; ② 当0.1
用三阶多项式对图6(a)的曲线进行拟合,获得以下拟合公式:
y1=-0.000 011 2x3+0.005x2-0.205x+0.994
(4)
式中:y1为初至纵波振幅Ap/激发纵波振幅A0比值;x为E/(S·kn).
2) 由图6(b)可知,弹性纵波波速vp/连续介质纵波波速理论值Cp随E/(S·kn)的增大而减小,具体减小规律为: ① 当E/(S·kn)≤0.1时,纵波波速衰减速率极小,衰减幅度不超过3%,vp/Cp接近于1; ② 当0.1
用四阶多项式对图6(b)的曲线进行拟合,获得以下拟合公式:
y2=0.000 003 16x4-0.001 4x3+0.058x2-0.28x+1.004 2
(5)
式中:y2为弹性纵波波速vp/连续介质纵波波速理论值Cp比值;x为E/(S·kn).
3 结语
1) 结构面法向刚度对岩体弹性纵波传播特性有重要作用,而结构面切向刚度对岩体弹性纵波传播特性几乎没有影响.
2) 依次固定结构面切向刚度为不同级大小(3 GPa·m-1到30 GPa·m-1),在每级取值下,逐渐增大结构面法向刚度,当结构面切向刚度不变时,初至纵波振幅和纵波波速皆随法向刚度的增加而增大,但增长速率逐渐减小,最终初至纵波振幅趋近于激发纵波振幅,纵波波速趋近于连续介质纵波波速理论值.
3) 考虑岩块杨氏模量E、结构面间距S与结构面法向刚度kn的综合影响,引入比值E/(S·kn),在保持kn/ks为2.5,同时改变结构面法向刚度kn与切向刚度ks时,初至纵波振幅和纵波波速都随E/(S·kn)的增加而减小,衰减速率经历极慢-变快-变慢-极慢四个阶段,以E/(S·kn)=0.1、1、10为界,最终Ap/A0减小至0.01,vp/Cp减小至0.67.

