应用BDLM的桥梁非均匀极值应力动态预测

樊学平，屈 广，刘月飞

(1.兰州大学西部灾害与环境力学教育部重点实验室，甘肃 兰州 730000； 2.兰州大学土木工程与力学学院，甘肃 兰州 730000)

0 引言

桥梁健康监测系统在长期运营中积累了大量监测数据，它包括均匀数据和非均匀数据，如何合理地处理这些数据是桥梁结构健康监测领域的主要困难之一，目前大量研究主要是基于均匀数据集中在模态参数识别、损伤识别、损伤评估、模型修正等领域[1-3].这些研究仍难以有效地预测和评估桥梁结构的动态响应行为，如： 预测均匀监测极值应力和非均匀监测极值应力.

本研究采用贝叶斯动态线性模型(Bayesian dynamic linear model，BDLM)在桥梁承载力和可靠性预测方面已取得一些研究成果，如采用动态线性模型实现桥梁退化承载力的模拟预测[4]； 采用应力的单一和组合贝叶斯动态线性模型以及一次二阶矩可靠度方法实现桥梁构件的可靠性动态预测[4-5].但在预测分析过程中存在以下问题需要进一步解决： ① 最优初始状态概率分布如何选择； ② 非均匀极值应力的动态建模问题； ③ 贝叶斯动态线性模型的监控机制问题.

鉴于上述问题，本研究基于非均匀监测得到应力信息并建立贝叶斯动态线性模型.考虑到初始状态信息概率分布的多样性，采用K-L准则选择最优初始状态概率分布函数，并利用折扣因子、单一贝叶斯因子以及累积贝叶斯因子提高和监控动态模型的预测精度，最后采用实例验证了所提模型和方法的合理性和适用性.

1 监测极值应力的动态线性模型

本研究的极值应力是从结构健康监测系统监测得到.其为每天所测应力的最大值信息.由这些极值信息回归得到的二次函数[6]，如式(1)所示，比线性函数[7]可以更合理地反映应力极值信息的趋势项变化规律，因而可以用来构造状态水平方程，如式(2)～(4)所示，极值应力的动态建模过程如图1所示.

h(t)=at2+bt+c

(1)

θt+1=h(t+1)=a(t+1)2+b(t+1)+c

(2)

θt=h(t)=at2+bt+c

(3)

θt-1=h(t-1)=a(t-1)2+b(t-1)+c

(4)

图1 极值应力的贝叶斯动态线性建模 Fig.1 Bayesian dynamic linear modeling of extreme stress

式中:h(t)为由极值信息回归得到的二次函数；a，b和c为监测极值应力的回归系数；t为监测时间，d；θt为第t天的极值应力状态值.

由式(2)～(4)，进一步可得

(5)

式中:Δt+1为t时刻到t+1时刻状态水平值的变化量.

考虑到监测极值应力的随机性和不确定性，基于状态信息和状态变化信息建立的非均匀极值应力动态线性模型如式(6)～(8)所示.式中的应力状态和状态的变化信息分别是指监测信息经过重采样方法(如： 五点三次平滑处理方法)得到的极值应力数据和重采样极值应力的变化数据.

监测方程：

yt+1=θt+1+νt+1,νt+1～N[0,Vt+1]

(6)

状态方程：

θt+1=θt+Δt+1+ωt+1, 1,Δt+1=(ri+1/ri)(Δt+2a)+ωt+1, 2,

(7)

初始状态信息：

(8)

式中：

yt+1为t+1时刻的应力监测极值；θt+1为t+1时刻极值应力的状态水平值；N[0·Wt+1]为正态分布函数；νt+1为监测误差项；ωt+1为状态噪声向量/状态误差向量；Dt为t时刻以及t时刻以前关于系统的信息集合，即：Dt={yt,Dt-1},Dt-1为t-1时刻的信息集，包括mt-1(平均值向量)，Ct-1(方差矩阵)等.另外，假设vt+1和wt+1相互独立，且都与θt+1独立，ri+1=ti+1-ti为采样时间间隔.

2 贝叶斯动态线性模型主要概率参数的确定方法

贝叶斯动态线性模型需要确定的主要参数包括Vt+1，Wt+1，mt和Ct.Vt+1可以通过监测极值应力和重采样极值应力的数据差近似估计.Wt+1可以通过折扣因子近似得到[6-7]，如式(9)所示.

(9)

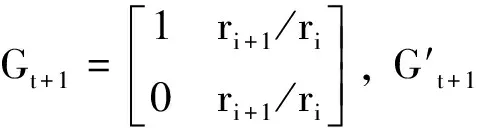
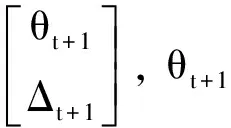
对于状态变量θt+1，有K-L信息距离：

(10)

式中:pRT, i(θt+1)为第i个关于θt+1的常规概率分布；pR(θt+1)为核密度估计得到的θt+1理论概率分布.但是由于核密度得到的理论概率度函数外延性不好, 所以要选择合适的常规概率密度函数来分析.

对于状态变化变量Δt+1，亦可以通过式(10)选择关于Δt+1最合理的常规概率分布函数.

3 动态线性模型的贝叶斯递推

图2 贝叶斯动态线性模型的概率递推过程Fig.2 Probability recursion processes of BDLM

贝叶斯动态预测模型[8-9]适合于对未来状态参数的预测和推断，其状态参数递推如图2所示.

贝叶斯动态线性模型的详细递推步骤：

1)t时刻状态变量的后验分布.

对于均值mt和方差矩阵Ct，有：

(11)

2)t+1时刻状态变量的先验分布.

(μt+1|Dt)～N[at+1,Rt+1]

(12)

3)t+1时刻监测变量的一步预测分布.

(yt+1|Dt)～N[ft+1,Qt+1]

(13)

式中:ft+1=E(yt+1|Dt)=mθt+(ri+1/ri)(mΔt+2a)，Qt+1=Var(yt+1|y1:t)=Rt+1, 1+Vt+1，pt+1=1/Qt+1为BDLM的预测精度.

4)t+1时刻状态变量的后验分布.

(14)

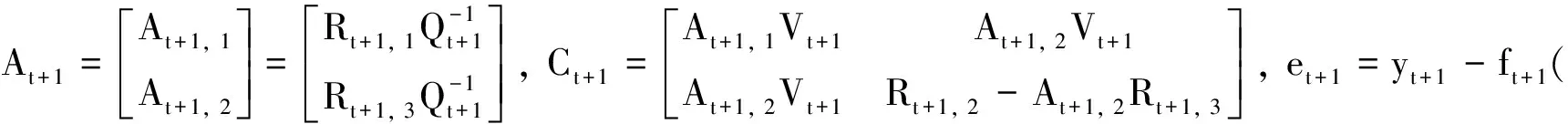
根据HPD区域的定义[1-2, 5]，对于监测值的预测区间(95%的保证率)为：

(15)

4 非均匀贝叶斯动态线性模型的监控机制

本研究主要通过建立贝叶斯因子对动态模型进行监控[4-9]，包括单一贝叶斯因子和累积贝叶斯因子.单一贝叶斯因子H(t)为：

(16)

式中:p0(yt|Dt-1)为一步预测监测变量的概率密度函数；p1(yt|Dt-1)为备择模型的PDF.

基于式(16)，可得累积贝叶斯因子为：

(17)

式中:Ht(k)是基于监测信息yt,yt-1, …,yt-k+1的p0(·)相对于p1(·)的k步累积贝叶斯因子.

式(16)进一步简化可得单一贝叶斯因子的具体表达式为：

(18)

模型监控准则[4-9]为：k=3时，H(t)小于0.15，则此检测值为异常值，需去除.异常值去除之后，可以通过累计贝叶斯因子的变化曲线来体现贝叶斯动态模型的预测精度，累计贝叶斯因子越大，说明预测精度越好，模型的不确定性越小.

5 算例分析

I-39北桥[10-11]建于1961年，对此桥横向第二跨钢板的跨中梁底极值应力进行了83 d的监测，其中前60 d为均匀采集，后23 d为非均匀采集.此位置应力集中比较明显，所以监测的应力数据，可以较好把握结构的安全状态[10-11].应力是由温度荷载、车辆荷载以及收缩徐变造成的, 桥梁自重造成的应力不包括在此应力信息中.前60 d均匀采集的数据如图3所示.

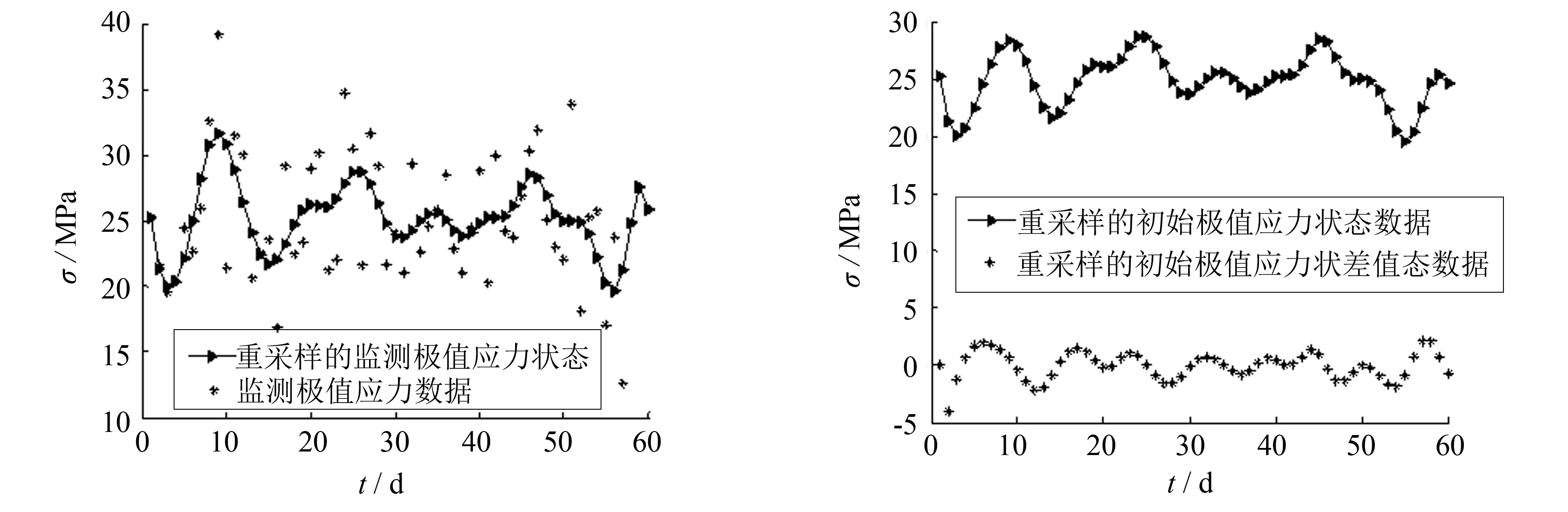
图3 平滑处理后的极值应力与监测极值应力对比 图4 平滑处理后的极值应力与对应极值应力差值对比

现采用前60 d均匀采集的极值应力数据，通过建立非均匀极值应力贝叶斯动态线性模型(如式(19)～(21)所示)，预测后23 d非均匀的极值应力信息.

为了得到初始状态信息的分布参数，采用五点三次平滑处理方法对前60 d的极值应力进行重采样.然后近似得到极值应力状态水平值和相对应的状态水平差值，如图4所示.

对水平值和水平差值分别进行了K-S检验, 可知水平值和水平差值都分别服从正态分布和对数正态分布，但通过K-L信息测度计算(式(10)所示)，水平值和水平差值的最优概率分布均为正态分布.因此建立的初始状态信息的概率分布如式(21)所示.

本算例基于式(1)～(8)，建立的贝叶斯动态线性模型为

监测方程：

yt+1=θt+1+νt+1,νt+1～N[0,Vt+1]

(19)

状态方程：

θt+1=θt+Δt+1+ωt+1, 1,Δt+1=(ri+1/ri)(Δt-0.002 294)+ωt+1, 2,

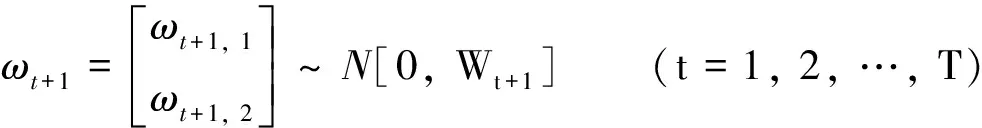
(20)

初始状态信息:

(21)

基于式(1)～(8)、式(11)～(15)、式(19)～(21)和图2，可得预测的非均匀极值应力和预测精度分别如图5～6所示，动态模型的预测应力与监测应力基本一致，而且预测精度越来越好.

图5 监测和预测得到的极值应力数据 图6 动态模型的预测精度

基于式(16)～(21)，可知单一和累计贝叶斯因子如图7～8所示.从图7可以看出单一贝叶斯因子均大于0.15，说明监测的极值应力均为正常值，即无异常值.从图8可以看出，随着监测应力的不断修正，累积贝叶斯因子越来越大，说明动态模型的预测精度越来越好，模型的预测不确定性越来越小.

图7 单一贝叶斯因子 图8 累计贝叶斯因子

6 结论

本研究提出了一种预测非均匀极值应力的贝叶斯动态方法，并给出对应动态模型的监控机制.通过实例验证得出： 预测的非均匀极值应力和监测的极值应力基本一致，而且预测精度越来越好, 并且监控机制对动态模型进行了很好的监控分析.本研究只提出桥梁构件非均匀极值应力的贝叶斯动态预测方法，而对于桥梁体系极值应力的动态预测方法有待进一步研究分析.