径向基函数配点法求解边坡降雨瞬态渗流问题
苏 燕, 洪黎丹, 张珑腾, 顾承宇
(1.福州大学土木工程学院, 福建 福州 350108; 2.台湾海洋大学河海工程系,台湾 基隆 20224)
0 引言
作为世界上受地质灾害影响最严重的国家之一,2016年我国共发生地质灾害9 710起,其中滑坡7 403起,占地质灾害总数的76.2%[1].前人研究表明,降雨入渗过程中,非饱和土边坡负孔隙水压力变化是导致其失稳的最主要因素[2-3].孔隙水压力不仅与降雨条件有关,也与坡面的土性参数、土层分布以及初始孔隙水压力有关.降雨入渗的过程将导致土体性质干燥状态的动态差异,在数值计算时极易形成病态矩阵,使计算结果不易收敛.基于网格单元的传统有限元法和有限差分法在模拟非饱和土渗流问题时,由于湿润峰的动态性,渗透系数以及饱和含水量的强非线性,容易使网格发生畸变和扭曲,常需要重构网格来解决,导致计算效率降低,甚至出现不收敛的现象[4].
针对降雨入渗条件下的边坡稳定性问题,学者们采用不同方法模拟非饱和土壤中的降雨入渗规律.罗渝等[5]利用有限差分法研究非饱和层降雨滑坡的运动特征.荣冠等[6]采用有限元法分析非饱和层土壤的降雨入渗机理.张社荣[7]结合强度折减技术,对非饱和层边坡的的瞬态渗流场进行求解.土壤水分特征曲线是影响非饱和层渗流变化的主要因素,学者们利用不同的渗流模型分析非饱和层土壤的瞬态渗流过程.甘永德等[8]运用Modified Green-Ampt模型,模拟土壤积水和非积水情况下的入渗过程.Cho等[9]基于Mein-Larson模型,提出了非饱和层湿润锋深度的计算方法.
径向基函数进行插值作为多变量逼近理论中的一种数值方法,具有形式简单、Euclidean距离各向同性,数值模拟结果与空间维数无关等优点[10].Hard等[11]提出了以多元二次曲面函数作为基函数的插值方法,即MQ插值法,用来求解不规则地形表面的二次函数方程.Kansa等[12]将离散数据拟合和函数近似的MQ插值法与配点型无网格法结合,用于处理拉普拉斯方程,称为MQ径向基函数配点法(multiquadric radial basis function collocation method,MQ RBFCM).这种方法现已在很多领域有着良好的应用.苏李君等[13]将MQ配点法与有限差分法相结合,用于数值模拟非饱和土壤的水分运动.为进一步研究边坡降雨入渗的瞬态渗流问题,针对非饱和层土壤特性的强非线性,本研究利用MQ配点法,建立一种数值计算模型,通过与前人的解析结果进行对比,验证其数值模型的准确性与稳定性.在此基础上,研究降雨入渗对非饱和无限边坡的渗流场影响.
1 数学模型
1.1 控制方程
Tracy[14]根据Gardner提出的土水特征曲线模型,将高度非线性的Richards方程进行线性化处理,得到一维线性化Richards方程:
(1)
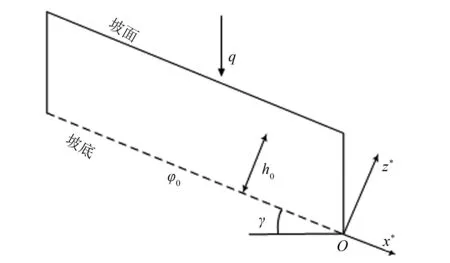
图1 均质无限长斜坡示意图Fig.1 Homogeneous infinite slope schematic diagram
式中:h*=eαgh-χ为线性化后的压力水头;χ=eαghd,hd=10-5为非饱和土极度干燥时的压力水头;Kθ=ks/(θs-θr),ks为饱和渗透系数,θr为残余含水量,θs为饱和含水量;Kαθ=Kθ/αg,αg为土壤孔隙大小分布系数.式(1)仅针对无限边坡成立,若考虑边坡倾角为γ的无限边坡问题,定义如图1所示的(x*-z*)坐标系,两坐标之间的关系为:
(2)
将式(2)代入式(1)得到:
(3)
1.2 边界条件
对于坡底边界,其压力水头恒定为ψ0,坡面为定流量边界,式中q为降雨入渗量即:
(4)
2 数值算法
2.1 MQ RBFCM
MQ RBFCM求解偏微分方程时,首先将区域离散成N个点,区域边界点满足边界条件,内部点满足偏微分方程, 建立N个代数方程.然后将待求解方程以径向基函数近似函数表示,将近似函数及各阶导数直接代入边界条件或偏微分方程,则可将偏微分方程转化为代数方程组进行求解N个待定系数[15].假定待求解偏微分方程问题为:

(5)
式中:L和B为微分算子.在控制域Ω内布置m个节点P1,P2, …,Pm,边界上∂Ω布置n个节点Pm+1,Pm+2, …,PN,然后令:
(6)
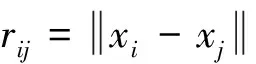
(7)
令N个节点各自满足式(7),得到N条方程,联立方程求解待定插值系数λj,然后代回式(6)得到方程u(x)的解.
2.2 控制方程及边界条件的离散

图2 布点示意图Fig.2 Point diagram
沿z*方向在控制域内布M个内部点,上边界下边界各布1个边界点,共布N=M+2个点,如图2所示.利用配点,将压力水头函数h*(z*)以MQ RBF形式离散为:
(8)

将离散后的压力水头函数h*(z*)代入控制方程和边界条件,得到离散后的控制方程和边界条件为:
(9)
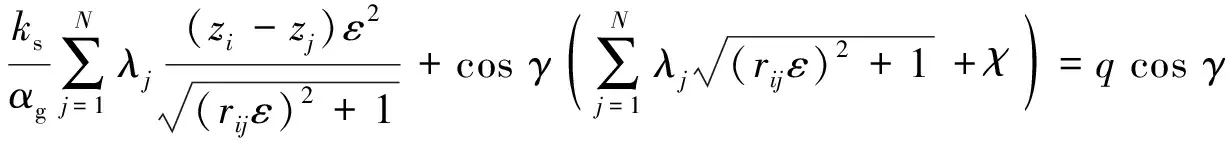
(10)
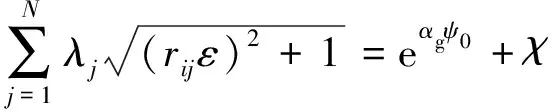
(11)
2.3 瞬态渗流问题的求解
对于瞬态渗流问题的初始条件,借鉴前人方法,对上边界施加一个较小的降雨强度qa,对边坡进行稳态分析来求得初始孔隙水压.根据M个内部点满足初始状态下的稳态控制方程,上下边界点满足各自的边界条件,联立可得N条方程,写为矩阵形式:
{[A1]M×N, [A2]1×N, [A3]1×N}T{λ1,λ2,λ3, …,λM,λ1+M,λN}T={d1,d2,d3, …,dM,f1+M,gN}T
(12)
式中:


(13)
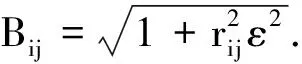
(14)
式中:H为系统矩阵,
(15)
根据已知初始状态和边界条件,可通过下式得到一组满足条件的待定插值系数λj:
(16)
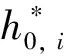
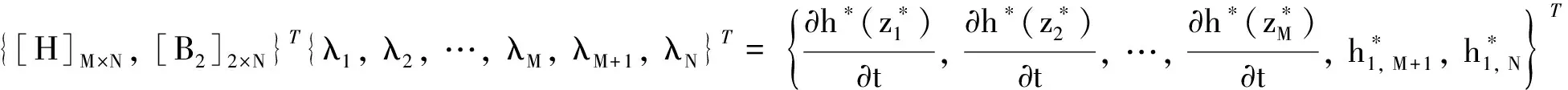
(17)

(18)
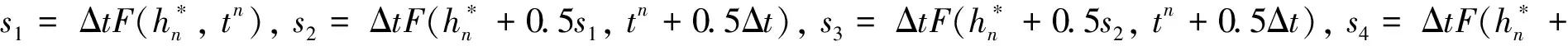
(19)
3 数值结果与讨论
3.1 均质无限边坡
1) 计算模型与参数.采用文[17]的无限边坡,如图1所示.斜坡土层的垂直厚度为2 m,斜坡水平长度为40 m,倾角γ=30°,饱和含水率θs=0.45,残余含水率θr=0.15,饱和渗透系数ks=1.0×10-4cm·s-1,土壤孔隙大小分布系数α=0.01 cm-1.
2) 边界条件.前期雨强为qa=2.8×10-11cm·s-1.边坡上边界边界条件为降雨定流量边界,降雨强度为qb.下边界为定水头边界,ψ0=-1 m.
3) 计算结果.当降雨强度qb为6.0×10-5cm·s-1小于ks和qb为3.0×10-4cm·s-1大于ks时,MQ RBFCM所得结果与前人的数值模拟及解析解所得的结果,在不同时刻的孔隙水压力沿斜坡面垂直方向的分布情况如图3所示.MQ RBFCM所得结果与前人的数值模拟及解析解吻合良好,表明运用MQ配点法求解无限边坡瞬态渗流问题是切实可行的.当降雨强度大于饱和渗透系数时,李宁等[17]利用解析解求得的积水时间为11.297 h,本研究计算求得的积水时间为11.260~11.265 h,两者的计算结果是比较接近的.
3.2 成层无限边坡
1) 计算模型与参数.采用文[16]的无限边坡, 如图4所示.成层斜坡中层1和层2的垂直厚度分别为1 m,斜坡水平长度为40 m,倾角γ=30°,如图5所示.计算中层1和层2土体采用的非饱和土参数分别为: 饱和渗透系数ks1=3×10-3cm·s-1,ks2=3×10-4cm·s-1, 土壤孔隙大小分布系数α1=α2=0.01 cm-1,饱和含水率均为0.45,残余含水率均为0.15.
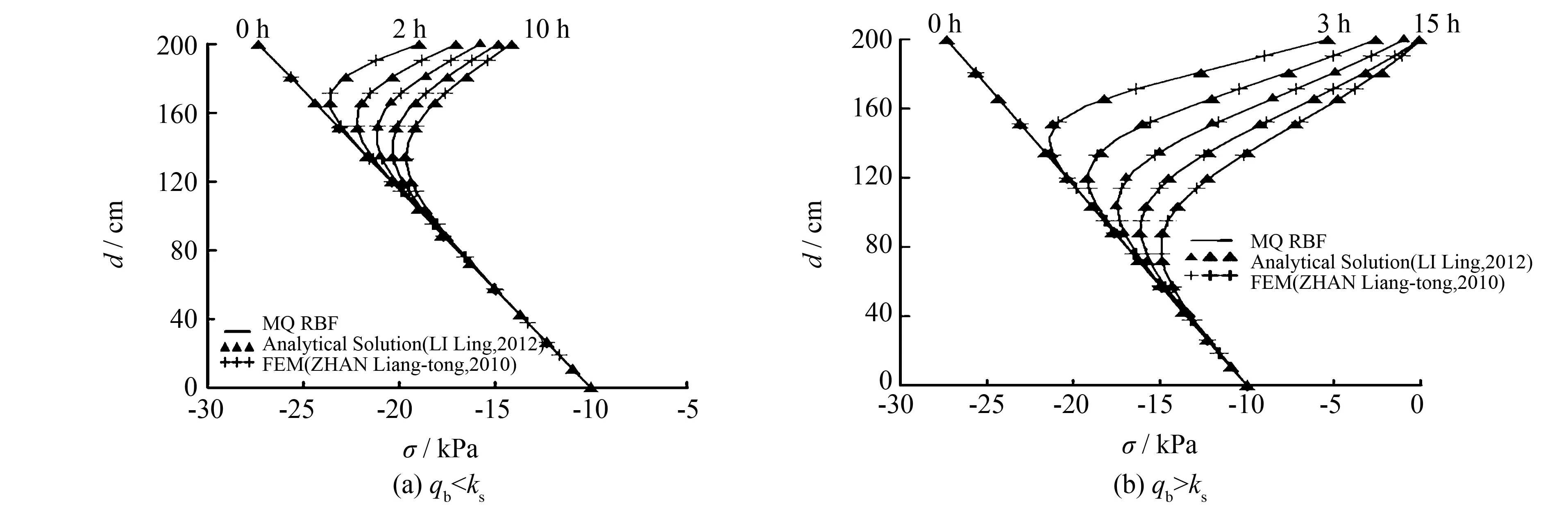
图3 不同时刻斜坡内孔隙水压力分布Fig.3 Distribution of pore water pressure at slopes in different time
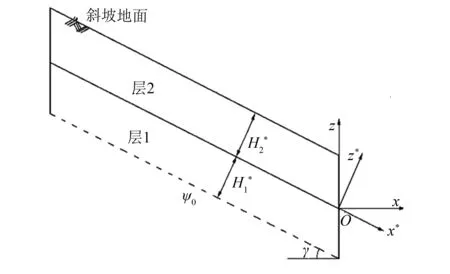
图4 双层斜坡示意图Fig.4 Sketch of double slope

图5 双层斜坡内孔隙水压力分布Fig.5 Pore water pressure distribution in double-layer slope
2) 边界条件.qa=3.0×10-3cm·s-1为获得初始负孔隙水压力分布的前期雨强,qb=1.08×10-3cm·s-1为后期降雨强度.模型上边界为定流量边界,下边界为定水头边界h=-1 m.
3) 计算结果.詹良通等[16]曾推导出成层斜坡降雨入渗的解析解.本研究参照文[16],利用MQ RBFCM对该问题进行求解,其结果对比前人解析解和有限元数值模拟计算结果可以发现,基本吻合如图5所示,说明了运用MQ RBFCM求解双层斜坡降雨入渗孔隙水压变化的可行性和正确性.
不同土壤渗透系数差异较大,变化范围为1~10-8m·s-1,将土层1改为渗透系数为0.1 cm·s-1的砂土,改变土层2土壤,其渗透系数为10-2~10-9cm·s-1.传统数值方法在求解互层土渗透系数差异较大时容易出现病态题,通过MQ RBFCM方法其条件数控制在1012以下, 如图6所示,说明本方法求解系统较为良态.将层1渗透系数定为10-1cm·s-1,层2为10-9cm·s-1,时间间隔为15 d, 历时90 d.孔压如图7所示, 与实际物理现象相符,说明MQ RBFCM方法能较有效解决互层土渗透系数的极端差异在传统数值方法中的病态问题.
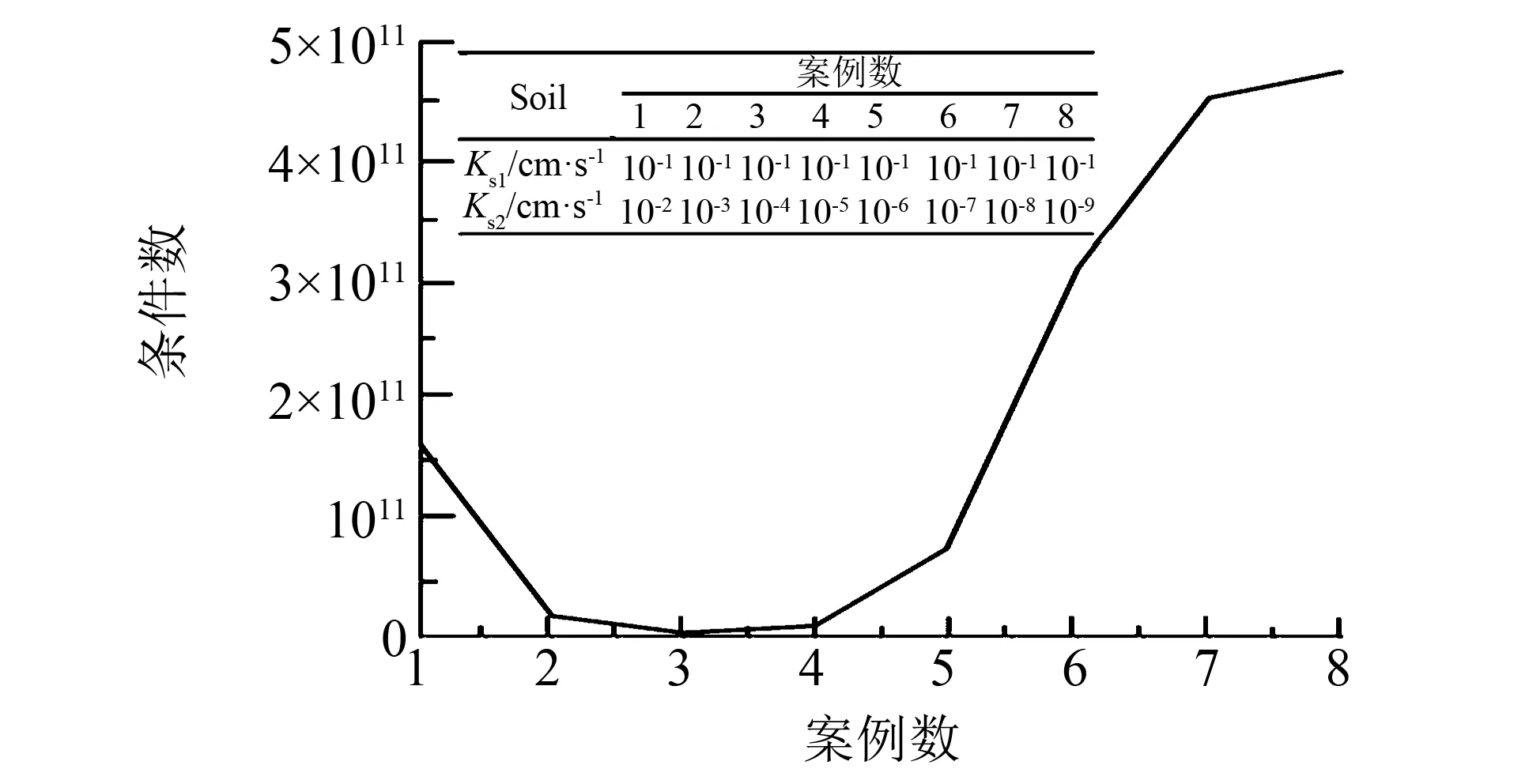
图6 案例1至8的条件数Fig.6 Number of conditions for Cases 1 to 8
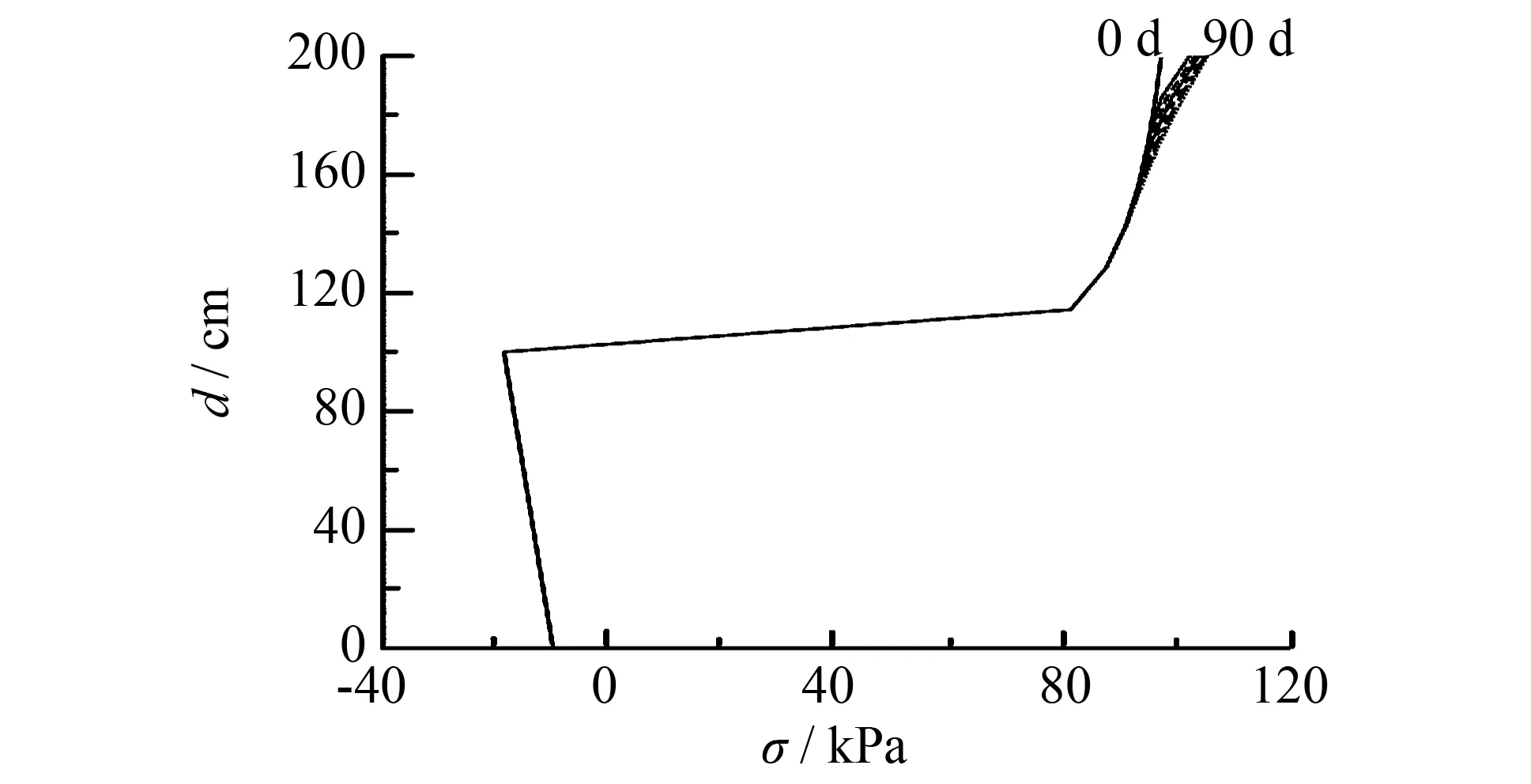
图7 双层斜坡内孔隙水压力分布Fig.7 Pore water pressure distribution in double-layer slope
4 结语
应用MQ 径向基函数配点法求解无限长斜坡在雨强小于及大于土体饱和渗透系数的情况,及渗透系数极端差异的互层土体的的渗流问题.该结果与解析解对比来看,本方法得到的孔隙水压力与解析解得到的水头相吻合.说明本方法对求解无限长斜坡渗流问题是正确的,可用于预测不同降雨强度下斜坡内孔隙水压力随时间的变化规律,以及非饱和土边坡稳定性分析.

