预定道路下的电动赛车转矩优化控制策略

李海鹏，彭育辉

(福州大学机械工程及自动化学院，福建 福州 350108)

0 引言

根据中国汽车工业协会公布的统计数据，以纯电动为主的新能源汽车2017年全年累计产销量分别为79.4万辆和77.7万辆，比2016年分别增长了53.8%和53.3%，我国已然成为全球最大的电动汽车市场.近年来，全球各主要汽车生产企业都调整未来发展战略，普遍认为以纯电动汽车为代表的新能源汽车是未来汽车工业发展的必然趋势.另一方面，为培养未来汽车工程师的创新和工程实践能力，自2013年由中国汽车工程学会主办的中国大学生电动方程式汽车竞赛(formula student electric China，FSEC)受到各高校的普遍关注和重视，到2018年已有59所高校报名参加该赛事.

驱动控制系统是电动汽车的核心部件，而控制策略又是驱动控制系统的灵魂，其性能的好坏直接影响着电动汽车整车的动力性和经济性.与混合动力或双电机驱动方式电动汽车相比较，目前普遍在用的单电机驱动纯电动汽车(如图 1所示)无法通过转矩分配的方式[1-2]，在保持动力性的同时提高经济性.

图1 单电机纯电动汽车整车结构Fig.1 Single motor PV structure

对于单电机纯电动汽车输出转矩控制策略的研究，最普遍的方法是基于模糊控制[3]，通过基础转矩和补偿转矩叠加的方式得出目标输出转矩.王立国[4]提出了一种基于加速踏板开度和输出转矩呈线性关系的转矩控制策略； 王佳等[5]则将加速踏板开度与电机转速作为输入控制转矩.以上两种策略简单、可靠，但是在动力性方面稍显欠缺，无法表达驾驶员的强加速意图.窦国伟[6]提出WTO补偿转矩，在加速踏板全开的情况下，增加转矩输出； 秦大同等[7]通过加速踏板开度变化率表征驾驶员加速意图，实现了不同程度的转矩补偿； 宋强等[8]在前者的基础上，还增加了对车速的考量，使汽车在低速时可以获得更大的输出转矩，这种转矩控制方式不仅提高了整车动力性，并且能够如实地表达驾驶员的加速强度意图，不足的是缺少了对整车经济性的考量.邓元望[9]提出一种基于基于驾驶员意图识别的转矩控制方法，将加速踏板开度转化的期望车速与实际车速进行比对, 获得车速偏差值，并根据车速偏差值及其变化率计算补偿转矩，提升了整车动力性与操控性； 陈龙等[10]将输出转矩策略划分为“常规”、“动力”、“经济”三种模式，兼顾整车的动力性和经济性，但并未提及模式之间的转换逻辑.徐凯等[11]在模式划分的基础上提出以SOC的高低作为急加速模式和一般加速模式之间的转换依据，但是这种双重模糊控制策略亦增加了控制逻辑的复杂程度和整车控制器运行出错的概率.

上述研究都是针对行驶工况不确定的情况，即所提出的转矩控制策略需要适应全路况的使用条件.然而，作为参加既定赛道比赛的电动赛车，比赛的行驶路径、道路行驶工况、里程等俨然成为控制策略的输入条件.本研究采用基准转矩与补偿转矩相叠加的基本思路，充分满足驾驶员的加速意图, 从而提高整车动力性.同时，为避免整车经济性过度降低，本研究根据已知赛道工况引入“参考SOC”变量，通过与实际剩余电量比对的差值，评估车辆的实时耗电情况，作出相应的补偿转矩调整，降低车辆由于耗电过量而无法完成比赛的可能性.所提控制策略能兼顾车辆动力性与经济性，核心内容包含： 1) 通过计算机仿真获取“参考SOC”曲线； 2) 根据“参考SOC”在线实时调整补偿转矩大小.

1 “参考SOC”曲线

图2 转矩控制的基本思路Fig.2 Torque control thought

“参考SOC”曲线，即理论上通过计算机模拟分析在既定赛道上完成比赛而随里程变化的最优电池SOC值.首先通过Matlab/Simulink搭建整车动力学模型，再利用道路模拟仿真软件Optimum Lap建立赛道模型，分析沿赛道分布的理想速度并生成“既定赛道工况”，将该工况输入整车仿真模型，从而获得整车在既定赛道上保证完成比赛所需要的“参考SOC”曲线，基本思路如图2所示.

1.1 整车仿真模型

根据比赛要求设定赛车性能参数，具体参数如下： 电机最高功率及额定分别为40和16 kW、电机最高转速为8 000 r·min-1、电机最大输出转矩为150 N·m、电池电压350 V、减速器传动比5.

通过Matlab/Simulink搭建的整车仿真模型，主要包括了以下4个模块： 驱动电机模块、动力电池模块、整车行驶模块以及驾驶员模块[12].

1) 驱动电机模块.根据电机外特性曲线，计算电机在当前转速下可输出的最高转矩，限制了驾驶员的需求转矩.同时，驾驶员需求转矩还受到了动力电池可提供的实际功率的限制.再根据电机效率特性图计算电机在当前电量下可输出的最高转矩，最后对比得出电机实际输出转矩.

Tmax=fext(nreal)

(1)

(2)

Tout=min{Treq,Tmax,Tach}

(3)

式中：Tmax为某转速下电机可输出最大转矩；fext为电机外特性曲线；Pach为动力电池可供功率；Tach为当前电量下电机可输出转矩；feff为电机效率特性图；Treq为驾驶员需求转矩.

2) 动力电池模块.首先经由电池放电曲线fdisch，可先计算相应端电压Eocv，然后计算获得电池可供实际功率[13].

Eocv=fdisch(SOCpre)

(4)

(5)

图3 rint等效电路模型Fig.3 Rint quivalent circuit model

式中： SOCpre为上一时刻电池剩余电量；Vlim为电池截至电压；Rb为电池内阻，由于内阻变化较小，取内阻值为常数.

电池SOC主要基于rint内阻等效电路模型[14](如图3所示)，通过下式计算实时电流Ireal和电池实时SOCreal.

(6)

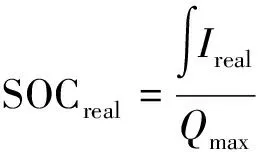
(7)

其中：Ireal为母线实时电流；Qmax为电池最高电量；Preq为需求功率.

3) 整车行驶模块.该模块描述了车辆在行驶过程中所受到的阻力、实时车速和行驶里程.

Tj=Tout·ηi·i-(Tr+Tw)

(8)

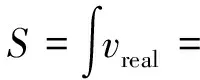
(9)

其中：vreal为实时车速；S为车辆行驶里程；δ为汽车旋转质量换算系数，取1.2.

4) 驾驶员模块.主要包括了两个部分，一部分为克服行驶阻力矩所需的转矩； 另一部分为根据实时车速与理想车速差异而计算的补偿转矩.

1.2 “参考SOC”曲线生成

根据既定赛道的实际行驶路径，通过Optimum Lap建立道路模型，通过计算机仿真获得赛道工况曲线，如图4所示.该道路模型反映了仿真车速分布情况.将赛道工况导入Matlab/Simulink整车模型，计算生成“参考SOC”曲线，如图5所示.可以看出A-B和C-D区域为明显的加速段，对应的SOC曲线斜率较陡，其余部分相对平缓，这是由于弯道较多，车速较低.

“参考SOC”曲线采用“行驶里程-SOC”的记录方式，相比于“行驶时间-SOC”的记录方式，在实车行驶时更具有合理性与精确性.由于驾驶员行为的不断改变，行驶时间也会随之变化，无法与“参考SOC”曲线相匹配，继而产生误差.而在这种行驶里程不变的情况下，“行驶里程-SOC”的记录方式使得仿真数据与实际数据有更高的匹配度.

图4 Optimum Lap仿真结果Fig.4 Simulation results of Optimum Lap

图5 参考SOC曲线Fig.5 SOC reference curve

2 实时在线转矩控制策略

图6 转矩控制策略算法框图Fig.6 Block diagram of torque control strategy

根据“参考SOC”与实际剩余电量的差值ΔSOC，将模糊控制规则分为以下三种： 1) 规则A强调动力性，补偿转矩较大； 2) 规则C则强调经济性，补偿转矩小； 3) 规则B则介于规则A与规则C之间.在驾驶过程中，随着ΔSOC不断递增，控制规则将逐渐从A过渡到C，以此降低电量消耗率，延长车辆可行驶里程，增加到达目的地的可能性.

就模糊控制器而言，这种简单的判断选择使得模糊控制器只有两个输入量，在使用快速原型生成底层代码时，能够方便通过二维查表的方式进行表征，减小了主控芯片的运算负载.

2.1 基准转矩控制策略

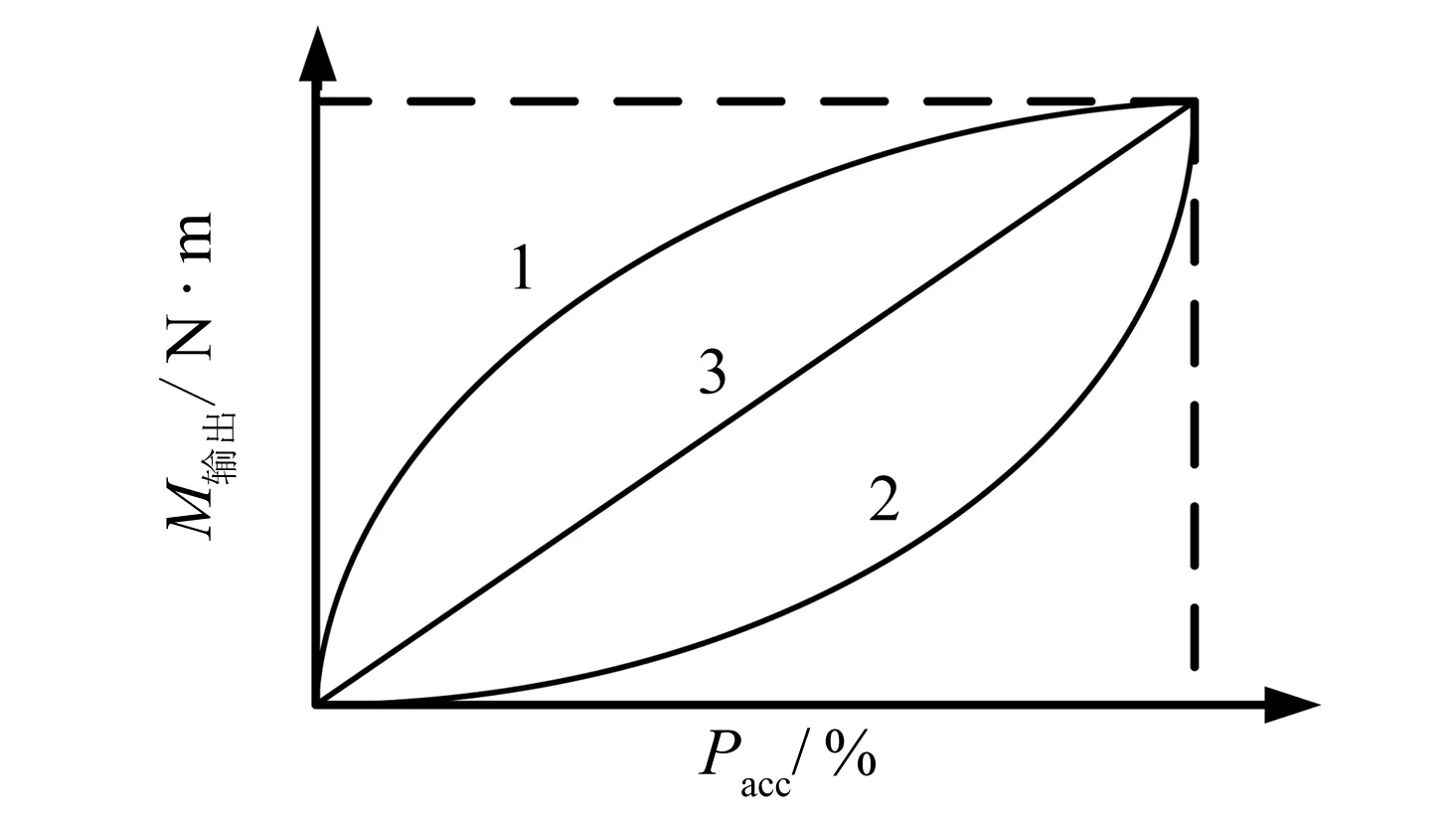
图7 基准转矩函数关系Fig.7 Functional relationship of basic driving torque

基准转距由加速踏板开度控制，直接影响整车动力性.根据转矩负荷系数为常量或变量，呈线性或非线性特征.而根据动力性和经济性的需求不同，非线性的函数关系又分为“上凸型”和“下凹型”，如图7所示曲线1和曲线2.

相较于1、2曲线所表达的非线性的函数关系，直线3表达的线性算法更加简单、可靠，加快了策略算法的运算速度.

2.2 补偿转矩控制策略

优化策略中的补偿转矩主要负责当驾驶员有强加速意图时，补偿电机的输出转矩以满足驾驶员需求，同时根据整车状态调整补偿转矩大小，以达到兼顾经济性的目的.

优化补偿转矩通过模糊控制算法实现，针对模糊控制器的设计主要包含了电机转速、加速踏开度板变化率、补偿转矩这三个变量的隶属函数设计以及相应的模糊推理规则排布.

(10)

补偿转矩突变对整车驾驶平顺性造成很大的影响，故为满足一定水平上的整车平顺性(最大冲击<15 r·min-3)，根据下式可得：

(11)

根据电机响应时间为20 ms，则电机最大补偿转矩为7.2 N·m.

将电机转速、加速踏开度板变化率、补偿转矩三个变量的模糊子集均分为5级: {小 较小 中 较大 大}，记作{NM NS ZO PS PM}.其中，考虑到整车在行驶过程中，电机最高转速不会超过4 000 r·min-1，并且电机效率MAP在大于4 000 r·min-1后，效率均大于90%(不考虑高转速低转矩输出状况)，故电机转速模糊集论域为[0 4 000]； 加速踏板变化率模糊论域取[0 10]，补偿转矩的模糊论域为[0 7.2].具体隶属函数如图8～10所示.

图8 加速踏板开度变化率隶属函数Fig.8 Membership function of pedal changerate

图9 电机转速隶属函数Fig.9 Membership function of motor speed

图10 补偿转矩隶属函数Fig.10 Membership function of compensation torque

为真实表达驾驶员加速意图，加速踏板开度变化率的论域划分相对均匀； 而电机转速分配在高转速部分的论域较广，对应电机在高转速期间的“高效区”较大.

根据实时剩余电量差值(如下式所示)的不同，模糊推理规则划分为以下三种情况：

ΔSOC=SOCref(S)-SOCreal(S)

(12)

其中： SOCref为参考剩余电量.

1) 当剩余电量差值在0%～3%时，此时动力电池电量被过度使用的情况较轻，主要强调整车动力性，推理规则如表1所示.

2) 当剩余电量差值在3%～7%时，此时电量被过度消耗，补偿转矩稍有下降，推理规则如表2所示.

表1 SOC差值小模糊规则

表2 SOC差值中模糊规则

表3 SOC差值大模糊规则

3) 当剩余电量差值在7%～10%时，此时电池电量出现严重的过度消耗，推理规则如表3所示.

从上述的模糊推理规则可以看出，输出的补偿转矩大小与加速踏板开度变化率成正比，如实地反映了驾驶员的加速意图； 而当电机出于低速运行的状态下，输出的补偿转矩较小，这样尽量规避了“低转速，高转矩”的电机低效区，提高电池电量的利用率.

3 转矩控制策略的试验验证

3.1 测试设备

试验在福州大学第一代电动方程式赛车E14上进行，如图11所示.控制策略采用北京华海科技快速原型(VCU)实现，编写控制策略模型生成相应代码并烧写入整车控制器中[15].数据以报文形式存储在广成科技CANRec模块上并采集包括电机转速、踏板行程、实时SOC、电机输出转矩、车速等数据.

3.2 测试方案

测试场地选取在某卡丁车场，全长500 m的赛道如图12所示.试验包含4组的实时动态对比测试： 第1组采用传统的转矩控制策略，只含有线性的基准转矩，不考虑补偿转矩； 在第2～4组试验中，采用本优化策略模式，分别在剩余电量差值在0%～3%、3%～7%、7%～10%三种情况下进行试验.每组驾驶方案以A点为起始点向左行驶，通过赛道两圈后，回到A点.采用全程驾驶时间表示该组的动力性，全程耗电量表征该组的经济性, 并通过比较各组加速踏板行程的平均值、标准差值来表达驾驶员的驾驶风格.

图11 测试用电动赛车Fig.11 The test Formula E

图12 试验车场空中俯视全景Fig.12 Overlook map of test site

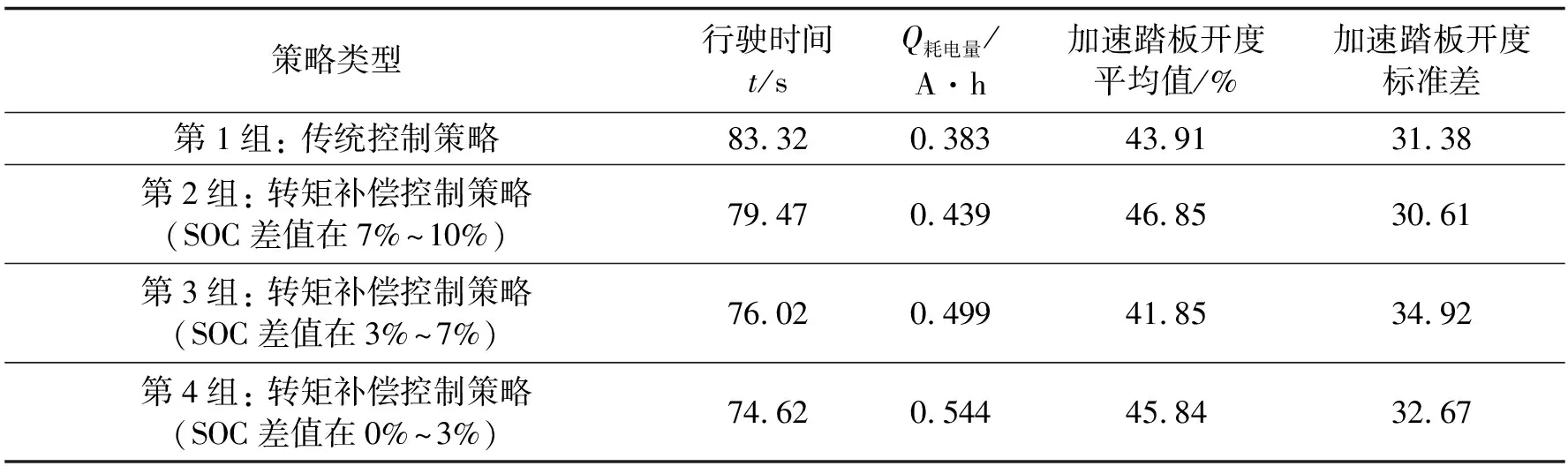
策略类型行驶时间t/sQ耗电量/A·h加速踏板开度平均值/%加速踏板开度标准差第1组: 传统控制策略83.320.38343.9131.38第2组: 转矩补偿控制策略(SOC差值在7%～10%)79.470.43946.8530.61第3组: 转矩补偿控制策略(SOC差值在3%～7%)76.020.49941.8534.92第4组: 转矩补偿控制策略(SOC差值在0%～3%)74.620.54445.8432.67

图13 耗电量曲线Fig.13 Power consumption curve

3.3 试验结果

由试验结果(如表4所示)可以看出，各组加速踏板行程平均值误差在5%以内，而标准差最大误差为4.31，故认为在本次试验中，驾驶员的驾驶行为风格并未出现较大的改变.动力性方面而言，后3组试验相较于传统的转矩控制策略，在行驶时间上缩短了4.62%，8.76%，10.11%.在经济性方面，后3组试验的耗电量比第1组分别多了14.62% 、30.29%、42.04%.

大约在7、20、45和57 s时，后3组试验的耗电量相较于第1组有明显的“上凸”趋势，刚好对应了A-B、C-D段直线加速部分.而其他部分与第1组试验基本平行，说明优化后的策略在加速意图并不显著的情况下，避免电机在低转速时大转矩输出的“低效状态”.

从4组的试验结果可以看出： 采用传统的线性控制策略，虽然耗电量较小，但是完全无法反映驾驶员的加速意图，特别是在A-B、B-C段，加速性能过低.而第3、4组试验数据，相较于第1组试验数据，动力性有了明显的提升.并且根据实车的耗电情况，以及预计耗电量，做出适当的转矩补偿，能够较好地提升整车的动力性能.

4 结语

1) 提出的优化策略通过模糊控制能够识别驾驶员的加速意图，增加补偿转矩能有效提升车辆动力性；

2) 基于计算机仿真的方式得到“参考SOC”曲线，并根据实际剩余电量与“参考SOC”的对比差值，能直观地反映当前车辆的耗电情况，并通过更换模糊推理规则的方式控制输出扭矩输出，降低因过度耗电而无法完成比赛的可能性.