基于低秩表示的判别特征提取算法
苏雅茹,许智杰,吴小惠
(1.福州大学数学与计算机科学学院,福建 福州 350108; 2.厦门大学航空航天学院,福建 厦门 361005)
0 引言
随着数据类型越来越丰富,数据结构也越来越复杂.比如,数据库文本、Web 数据、各种各样的图像数据和视频数据等,这给数据的分析、处理和应用带来了困难与挑战.这些数据往往具有很高的维数和复杂的结构,数据形式通常是稀疏的,带有大量的冗余信息,数据的这些特点不仅增加了分析处理负担,使得时间和空间复杂度迅速上升从而导致算法性能下降,甚至容易掩盖数据的真实结构从而导致错误的分析处理结果.高维复杂数据的诸多应用需求使得对高维数据的分析处理在科学研究领域占据着越来越重要的地位.
充分利用高维复杂数据的结构对学习问题进行建模是利用数据信息的关键所在.关联矩阵是描述数据结构的一种形式,用于度量样本和样本之间的相关性.相关性高的样本通常会被聚集到一块,关联矩阵的理想表现是假设样本按类别排好,其对应的关联矩阵是块对角矩阵.近年来,利用低秩表示构造的关联矩阵被应用于聚类[1-6]、维数约简[7-9]、噪声人脸识别[10]、闭塞人脸识别[11-12]等问题,并取得很好的效果.
本研究提出一种低秩表示判别映射(low-rank representation discriminant projections,LRDP),基于低秩表示(low-rank representation, LRR)构造关联矩阵并用于判别特征提取,并利用人脸数据集的实验证明了LRDP的特征提取有效性.
1 低秩判别映射
首先,给定一组来自若干相邻子空间的样本,低秩表示把样本向量看成其它所有样本向量的线性组合,并寻找最低秩表示,低秩表示的构造特点决定了LRDP的良好数据全局结构表达能力和判别结构表达能力[1].然后,基于表达数据关系结构的低秩表示引入充分利用数据判别信息的判别准则,这些特点使得LRDP很好地利用了数据样本信息.
1.1 低秩表示
低秩表示的数学描述如下[1]:
给定一个样本集X=[X1,X2, …,Xn]∈Rd×n,n表示样本个数,d表示样本维数,每个样本Xi∈Rd都可以表示为“字典”A=[a1,a2, …,am]中的基的线性组合,则模型描述为:
X=AZ
(1)
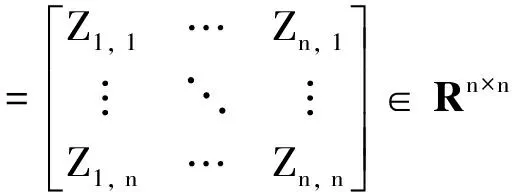
其中:Z=[Z1,Z2, …,Zm]是一个由系数向量组成的系数矩阵,系数向量Zi对应着样本Xi.
因为A的复杂性,样本集X的系数矩阵Z通常有多个可行解,上述模型可以通过以下的优化问题来求解:
其中: “最低秩表示”Z*表示最优解.
由秩rank(Z)的非凸性,上述模型的优化问题通常很难解决.于是,采用矩阵计算方法[13-14],优化问题(2)可以替换为以下凸优化问题:

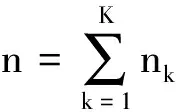
(4)
经过理论证明[1],当满足两个条件: 样本数据充足,即nk>rank(Xk)=dk,且子空间独立时,优化问题(4)可以得到一个块对角阵解:

(5)

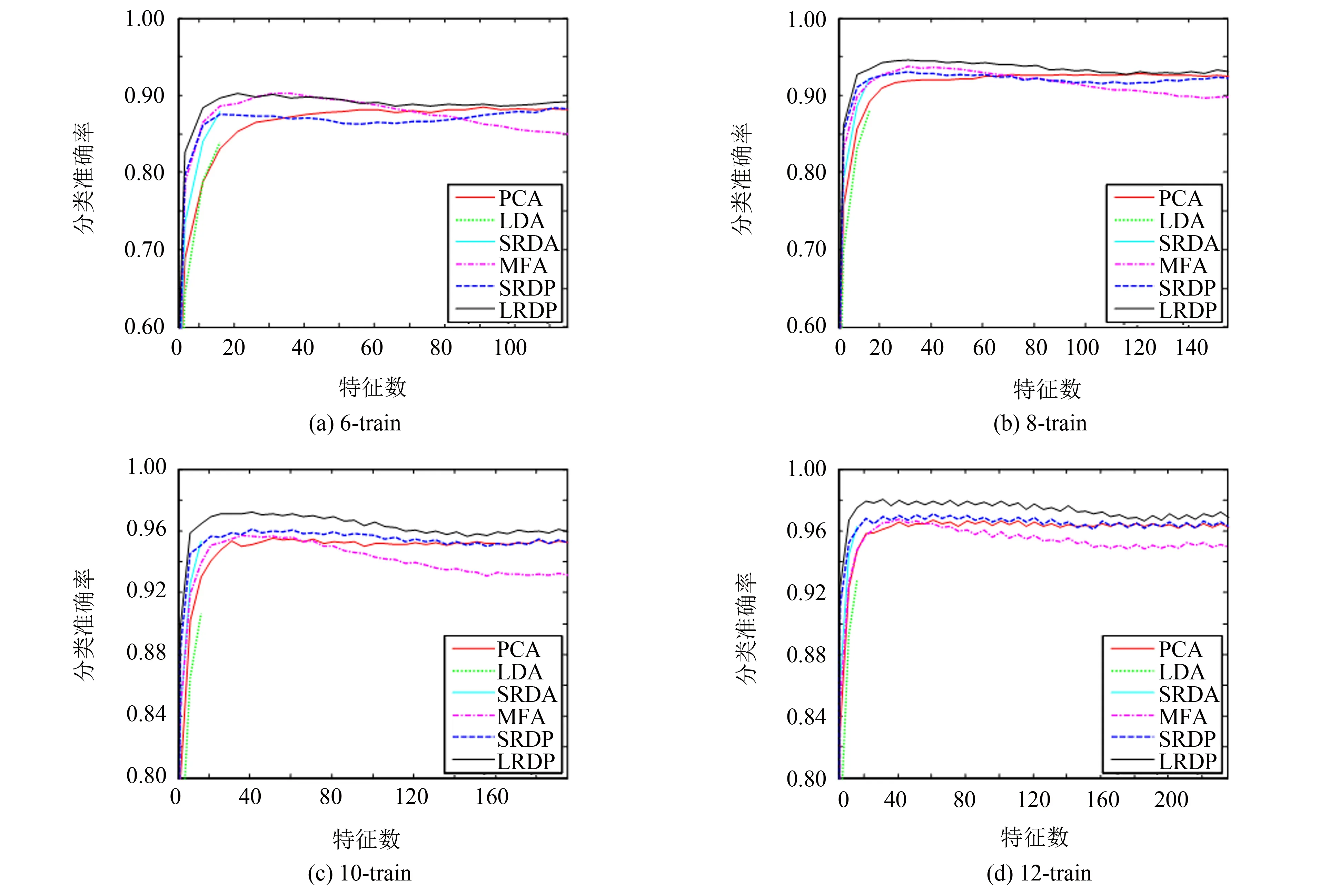
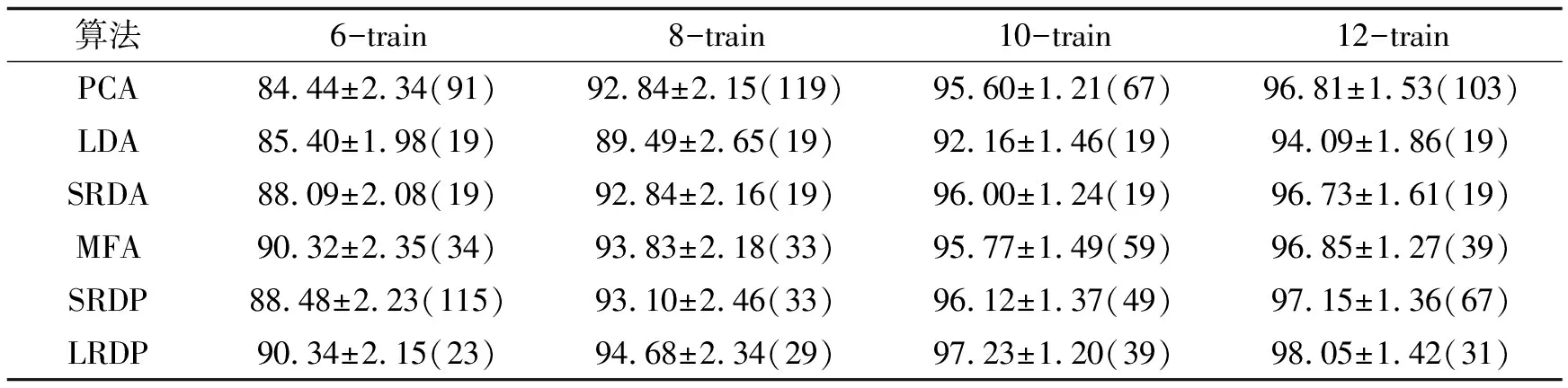
低秩表示用样本自身来表示数据向量,其原因是解空间为I-null(X),当rank(X) 给定样本集X=[X1,X2, …,Xn]∈Rd×n,假定均值为零,包含K个类别的样本,并得到最低秩表示Z*: (6) 定义样本Xi的最低秩表示向量:Zi=[Zi, 1,Zi, 2, …,Zi, n]T,并设k个类别中的第l个样本的最低秩表示向量为Zkl. 给定线性映射Y=VTX,对于单个样本Xi∈Rd,可以从d维空间映射到dr维空间,得到Yi∈Rdr; 对于样本集X,也可以从d维空间映射到dr维空间,得到Y,其中dr< 定义映射空间样本集的类内残差: (7) 其中:δk(Zkl)实现只保留最低秩表示向量Zkl中第k个类别的所有样本系数的功能. 同时, 定义映射空间样本集的类间残差: (8) 其中:δk′(Zkl)实现只保留最低秩表示向量Zkl中第k′个类别的所有样本系数的功能. 判别准则的目标是尽量减小类内残差并尽量增大类间残差,通过最大化以下目标函数来实现: (9) 其中:β系数用于平衡类内残差和类间残差. (10) (11) J(V)=tr(VT(βRB-RW)V) (12) (13) 采用拉格朗日乘子法求解上述目标函数: (14) (15) 其中,λ是拉格朗日乘数.那么 (βRB-RW)Vi=λiVi (16) 其中:λi(i=1, 2, …,d)是(βRB+RW)和XXT的广义特征值,Vi(i=1, 2, …,d)是相应的广义特征向量. 表1 低秩判别映射 低秩判别映射(LRDP)的算法步骤如表1所示. 为了对比低秩表示和稀疏表示对数据结构的表达能力,提出一种基于稀疏表示的判别特征提取算法-稀疏表示判别映射(sparse representation discriminant projections, SRDP).SRDP和LRDP的不同在于,SRDP的样本关联矩阵是基于稀疏表示构造的, 而LRDP基于低秩表示.稀疏表示可以通过以下的凸优化问题求解[16-17]: (17) 表2 Yale、UMIST数据集 本实验采用Yale和UMIST人脸数据集, 数据集信息如表2所示.实验数据集被分为训练集和测试集两部分,假设实验为P-train,则每类随机取P个样本作为训练样本,其余作为测试样本.实验要选择合适的P值,因为P值太大信息不充分,太小容易过拟合. 对每组实验数据,分别采用主成分分析(PCA)、线性判别分析(LDA)、谱回归判别分析(SRDA)、边沿Fisher分析(MFA)、SRDP、LRDP六种算法进行特征提取,统一采用SRC分类方法的分类准确率来评价各种特征提取算法的性能.为了准确地评估六种算法的性能,对每个P值进行20次随机实验,并取20次随机实验的分类准确率的平均值作为分类准确率. 假设样本类别数为K,样本数为n,则LDA和SRDA最多可以取K-1个特征,而其它算法的特征数可以达到n-1.实验结果给出了分类准确率(分类性能)随特征数变化的曲线图(详见图1~2),并在表3~4中给出最佳分类准确率(最佳分类性能)、相应的标准差和特征数. 图1 Yale数据上分类性能随特征数变化的曲线Fig.1 Recognition accuracy vs.feature dimension on Yale data set 算法4-train5-train6-train7-trainPCA69.19±4.44(58)73.42±3.99(73)77.80±3.40(87)79.50±4.96(97)LDA67.67±6.11(14)72.83±3.13(14)75.93±5.24(14)78. 02±3.80(14)SRDA68.76±4.91(12)73.37±2.97(14)78.40±5.07(14)80.01±4.04(14)MFA67.86±4.37(12)71.94±5.56(16)73.87±4.25(16)75.17±5.16(20)SRDP68.86±4.34(59)73.49±3.95(74)78.13±4.06(89)79.25±3.88(96)LRDP73.81±4.31(47)77.50±3.66(65)82.47±3.46(66)84.03±4.81(94) 从图1~2可以看出,LRDP的性能几乎总是优于其它的算法.对各个P值,各个算法在特征数比较少时,分类性能随着特征数的增加而快速上升,当特征数达到一定值后,性能上升变得缓慢甚至有少许下降,说明随着特征数的增加,判别信息的增加变得不明显,其原因为受到冗余特征的负面影响.随着P值的增加,即训练样本数的增加,各个算法的性能都有一定的提高,说明训练样本的特征是判别信息的主要来源.从表3~4可以看出,LRDP最佳性能总是优于其它算法(包括MFA). 图2 UMIST数据上分类性能随特征数变化的曲线Fig.2 Recognition accuracy vs.feature dimension on UMIST data set 算法6-train8-train10-train12-trainPCA84.44±2.34(91)92.84±2.15(119)95.60±1.21(67)96.81±1.53(103)LDA85.40±1.98(19)89.49±2.65(19)92.16±1.46(19)94.09±1.86(19)SRDA88.09±2.08(19)92.84±2.16(19)96.00±1.24(19)96.73±1.61(19)MFA90.32±2.35(34)93.83±2.18(33)95.77±1.49(59)96.85±1.27(39)SRDP88.48±2.23(115)93.10±2.46(33)96.12±1.37(49)97.15±1.36(67)LRDP90.34±2.15(23)94.68±2.34(29)97.23±1.20(39)98.05±1.42(31) 本研究利用低秩表示和判别准则,提出低秩表示判别映射LRDP.经过理论分析和对比实验,发现存在以下三个因素: 1) 在子空间独立的假设下,通过低秩表示获得关联图,其类内关联系数大,类间关联系数小,表现出一定的判别结构表达能力; 2) LRDP和SRDP都不是采用标准基作为基函数,而是利用样本自身作为基函数,稀疏表示单独为每个样本寻找稀疏表示,而低秩表示对所有样本寻找低秩表示,因此,低秩表示对数据全局结构的表达能力比稀疏表示更强; 3) 采用缩小类内残差和增大类间残差的判别准则,更好地利用了样本的类别信息.有鉴于此, 本研究认为LRDP具有良好的稳定性和鲁棒性.总之,LRDP是一种有效的特征提取算法,是一种全局性算法,同时还有较强的判别性,能够比较准确地描述数据集的全局结构和数据样本的判别关系.下一步工作将考虑引入一些约束,用非凸替换来求解目标函数,或者从矩阵扩展到张量形式的分析.1.2 目标函数



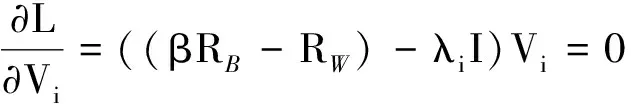

1.3 低秩判别映射(LRDP)


2 实验结果与分析



3 小结

