集值优化问题强有效元的二阶Kuhn-Tucker最优性条件

余 丽

(宜春学院数学与计算机科学学院, 应用数学研究中心，江西 宜春 336000)

0 引言

集值优化问题的研究离不开有效解，近年来对有效解的研究取得了丰富的成果[1-5].另一方面，集值映射的导数被相继引出且广泛应用到优化问题的最优性条件[6-10].Corley[6]在实赋范线性空间中借助切导数的性质建立了一阶Fritz John必要最优性条件.最近，不少学者相继研究了二阶(高阶)最优性条件.Jahn等[7]引进了二阶上图导数的概念，建立了集值优化的二阶必要最优性条件.然而，在典型的Kuhn-Tucker型最优性条件中，目标函数的导数与约束函数的导数不能分开，为此，文献[10]引进了一种新的二阶切上图导数，并借助该导数建立了集值优化问题弱有效元的二阶最优性条件.

1 基本概念与引理

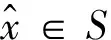
定义1[11]设E⊂X，集值映射F:X→Y称为在E上是近似C-次类凸的，如果clcone(F(E)+C)是凸的.

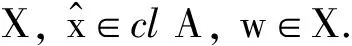
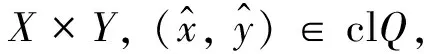
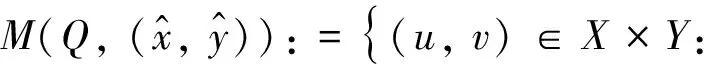
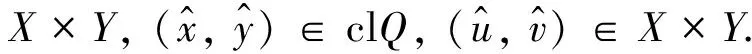
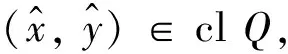
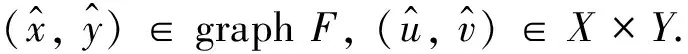
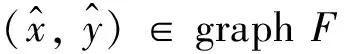
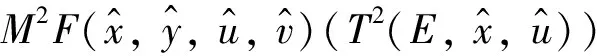
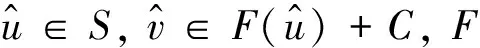
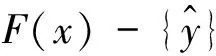
定义6[4]设B为C的基，N(0Y)是Y的零点邻域基，点y∈M⊂Y称为M关于锥C的强有效点，记为y∈GE(M,C)，如果∀φ∈Y*, ∃U,V∈N(0Y)，使得φ[clcone(M-y)∩(U-cone(V+B))]有界.

引理4[1]设Y为局部凸的拓扑向量空间，序锥C是点凸锥，且存在有界基B.如果Ø≠M⊂Y，则

GE(M,C)=GE(M+C,C)

引理5[14]Bst具有性质： 1)Bst≠Ø； 2)若B是C的有界基，则Bst=intC*.

设F:X→Y,G:X→Z为集值映射，考虑下面集值优化问题(VP)

minF(x), s.t.G(x)∩(-D)≠Ø,x∈X

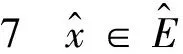
2 二阶最优性条件

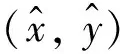
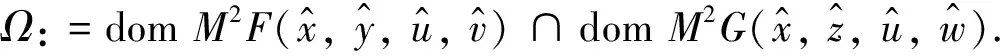
s*(y)+k*(z)≥0

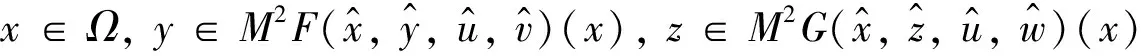
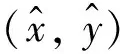
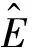
(1)

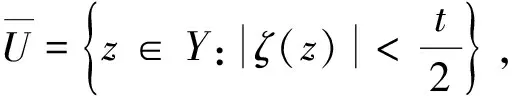
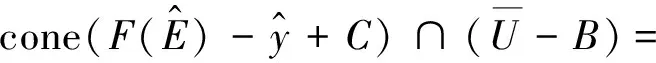
Ø

(2)

Ø

(3)

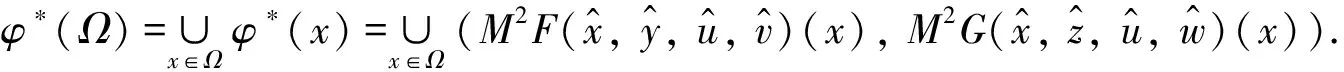
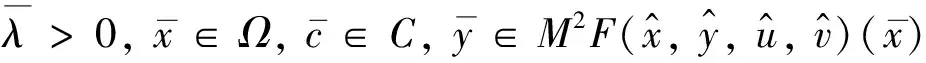
(4)

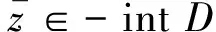
⊂-intD(∀n>N1)

(5)

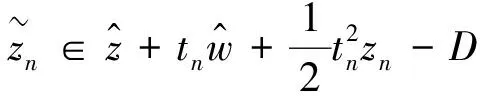
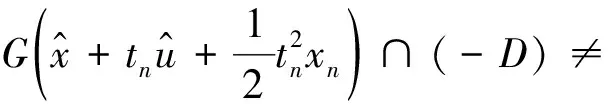
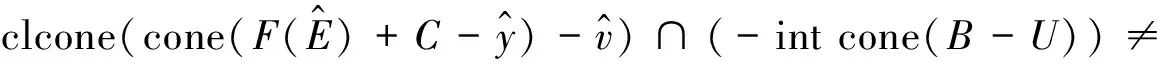
由文献[9]中定理2.1可知:

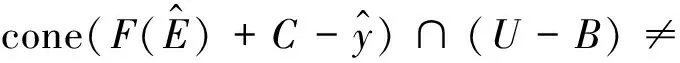
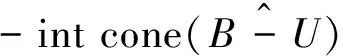
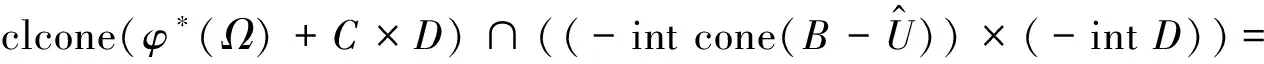
由假设φ*(x)在Ω上是近似(C×D)-次类凸的，于是clcone(φ*(Ω)+C×D)是凸的.由凸集分离定理知存在(s*,k*)∈Y*×Z*{(0Y*, 0Z*)}使得

(6)

由clcone(φ*(Ω)+C×D)为锥及(s*,k*)在其上有下界，于是

(s*,k*)(clcone(φ*(Ω)+C×D))≥0

(7)

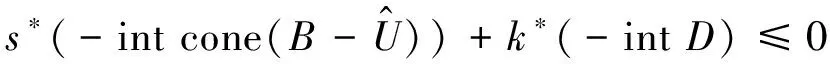
(8)

由(0Y, 0Z)∈C×D及式(7)得(s*,k*)(φ*(Ω))≥0.即

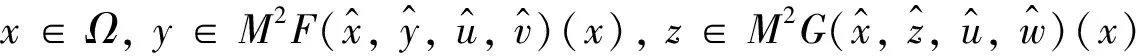
下面证明s*∈Bst∪{0Y*},k*∈D*.当s*≠0Y*时，由式(8)得

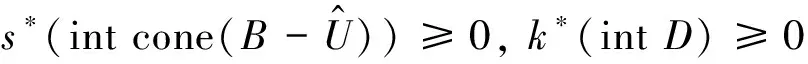
因此

⊂intC*,k*∈(intD)*

(9)

由B是有界基及引理5知s*∈Bst，于是由式(9)得k*∈D*，定理得证.

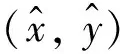
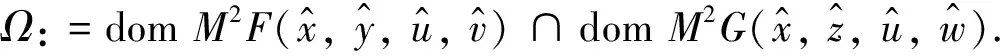
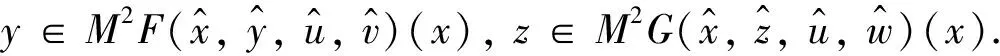
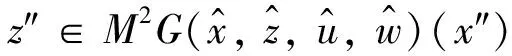
k*(z″)<0

(10)

另一方面，由已知条件和s*=0Y*，结合定理1可得:

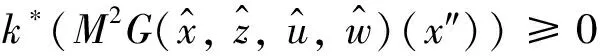
此与式(10)矛盾，故定理成立.

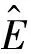
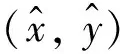
无界.取k>0,δ>0，令

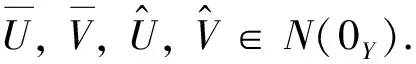
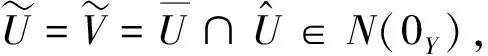
(11)

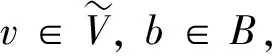
s*(un-μn(vn+bn))→-∞

(12)

由式(11)～(12)可知存在一正整数N，使得

(∀n≥N)

(13)

特别有tN>0且

(14)

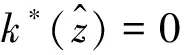
(15)

且

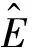
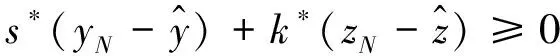
此与式(15)矛盾，故定理得证.