考虑用餐约束的城市轨道交通乘务计划编制优化研究

潘寒川，刘志钢，吴 强，胡 华

（1.上海工程技术大学 城市轨道交通学院，上海 201620；2.上海地铁第二运营有限公司，上海200063)

0 引言

乘务计划是城市轨道交通运营管理的重要组成部分，良好的乘务计划既能减少运营成本，又能保证列车运行安全。随着列车发车间隔的缩短、运营里程的增加及运营时间的延长，乘务计划的编制过程变得十分复杂。同时，我国城市轨道交通乘务员运用中普遍存在的“乘务员用餐”约束又进一步加深了问题的复杂度，使得西方主流的一些模型和算法在国内实施面临困难。如何合理地处理“乘务员用餐”约束，优化乘务员作息时间，提高乘务工作效率已成为事关城市轨道交通运营安全和效率的重要课题。

由于乘务员在列车上不允许用餐，管理部门在线路中设定若干具有设备条件的站点作为用餐点，乘务员在用餐点下车进行用餐。当乘务员下车用餐时，必须安排其他乘务员接替当前乘务员驾驶列车。传统的乘务计划编制过程中，这部分乘务员被定义为“替饭乘务员”，其每天的工作任务很可能仅完成替饭任务后便回车场休息，工时利用率较低。同时，与此形成鲜明对比的是部分乘务员被安排的工作量较大，乘务员的疲劳度较高，影响行车安全。

近年来，乘务计划编制的优化越来越引起相关学者的重视。例如，郑玢[1]提出了一种基于列生成算法的乘务员分配模型，使得排班人员的工作时间和工作量大大减少；Caprara等[2]讨论了铁路乘务计划编制的分阶段问题，提出一种集合覆盖模型，并设计了有效算法，通过实际案例验证了模型的有效性和实用性；张增勇[3]提出了基于惩罚费用的城市轨道交通乘务排班优化模型与算法；丰富[4]构建了考虑时间均衡度的城市轨道交通乘务排班计划模型；李子卿[5]研究了应对特殊情形下的城市轨道交通乘务排班问题，并建立策略约束优化模型；石俊刚等[6]研究了多线乘务员共享条件下城市轨道交通乘务计划均衡编制问题；张苏波等[7]研究了乘务派班模型构建及计算机软件应用开发；李献忠等[8]在引入乘务广义费用的基础上用禁忌搜索算法优化城市轨道交通乘务排班问题。从以上的研究现状可以看出，针对乘务计划的研究成果较多，但考虑“乘务员用餐”约束的直接相关研究较少，因而针对“乘务员用餐”约束进行研究，以期为运营企业提高乘务员运用效率、增强精细化管理水平提供理论参考。

1 乘务计划编制的主要影响因素

1.1 列车运行图

列车运行图是乘务计划编制的基础，各条线路根据自身的客流特征，每天各时段的上线列车数具有一定的差值。分时上线列车数示意图如图1所示。

图1 分时上线列车数示意图Fig. Vehicle count for different times

替饭、早高峰、晚高峰所需最少上线列车数分别为Nm，Ne和Ns。实际运营计划编制过程中，由于公司管理等因素，往往采取固定班组的形式。因此，每个班组配备的人数为他们当中的最大值，这样无形中造成了一定的人员浪费及乘务员工作量的不均衡(平峰期利用率较低)。

1.2 乘务驻点

乘务驻点一般指乘务员可以下车停留的车站，一般分为：①出退勤地点。出退勤地点指允许乘务员出勤或退勤的车站，乘务员不得在出退勤点以外的车站出勤或退勤。②轮乘点。轮换休息地点指可供乘务员下车短暂休息的车站，乘务员在轮乘点下车休息时，会安排其他乘务员接替当前乘务员驾驶的列车，当前乘务员休息一段时间后，再接替其他乘务员，继续执行列车驾驶任务。③用餐点。用餐点指允许乘务员下车用餐的车站，用餐车站需设立相应的食堂供乘务员用餐使用。乘务员在下车用餐时，应安排替饭乘务员接替当前乘务员驾驶列车，当该乘务员用餐结束后，再接替其他用餐乘务员，继续执行列车驾驶任务。

乘务驻点的设置会受到设施设备(如设立为用餐点的车站必须建设食堂等场所)、企业管理(如一般出退勤地点与班组长办公室设立在一起便于班前培训)、车站性质(如折返站由于需双乘务员折返可设立为轮换休息)等因素的影响。在基础条件允许的情况下，一般将用餐点、轮乘点等设置为同一车站，也即功能集中车站。这样的设置对于乘务排班来说存在便利和优势，部分乘务员可在出勤前或出退勤后安排就餐，这样避免在中途安排用餐，可提高乘务员利用效率。

实际情况下，由于车站内部空间的限制，不同功能的乘务驻点都分别设置在不同的位置。以某线路的A站、F站设置为轮乘点，C站和D站分别设置为用餐点和出退勤点为例，可行任务号如图2所示。图2中蓝色线条为列车运行轨迹，红色线条为可供乘务员执行的一个计划，这个计划为依次执行任务段L1，L4，L5，L8，L9，L10，L11。可以看出，乘务员在驾驶1101次列车到达A站后休息了2个间隔后继续驾驶1106次列车。图2中蓝色背景的区域为用餐时间(C站为用餐点)，当乘务员执行完L8到达C站后下车进行用餐，用餐结束后继续执行L9。图2中灰色背景的区域为交接班时间(D点为交接班点)，该乘务员执行完L11后在D站下班。

图2 可行任务号示意图Fig.2 Number of a feasible task

由图2可以看出，C站在用餐时间段(蓝色区域)内必须保证一定数量的替饭乘务员来确保就餐乘务员的用餐时间，而在非就餐时间段(非蓝色区域) C站是没有乘务员进行等待的。这部分替饭乘务员每天的执勤任务仅仅为“跑替饭圈”，其他时间没有任务执勤，任务量较低。同时，由于我国轨道交通大部分企业均采用“走行公里数”的绩效来计算工资，乘务员的薪酬工资也出现不均衡现象。

随着我国城市轨道交通运营里程的不断增加，发车间隔的不断缩短，单一用餐点已经很难满足实际运营的需求。当上线列车数大于(Me-Ms) /Ic时，其中Me为起始用餐时间，Ms为结束用餐时间，Ic为列车在C站的发车间隔，需设置多处用餐点进行用餐。

多就餐点就餐主要以“地点优先”为原则，即在用餐时间内到达线路中任一就餐点立刻进行就餐。设定C站和D站为“就餐点”，使用红色表示需用餐的运行线，下行方向(A→F方向)列车到达C站即进行就餐，上行方向(F→A方向)列车到达D站进行就餐。多用餐点就餐示意图如图3所示。

1.3 轮转规则

轮转规则即管理人员按照指定轮转制度(六班四转、四班两转等)将任务号分配给乘务员，形成一个周期(一般为一个月)的阶段任务[9]。例如，目前我国城市轨道交通最常用的“四班二转”的轮转规则为：白班、夜班、休息、休息。“夜班”工作时间跨越2 d，事实上“四班二转”中第1个休息日，并非完全休息，而是在当日凌晨4 ∶ 00—8 ∶ 00之间需要完成一定的驾车任务。因此，“四班二转”轮转规则实际为白班、夜班、早班、休息，其中夜早班需要连乘完成，乘务员夜间留宿在车场。“四班二转”基本作业时间如表1所示。

表1 “四班二转”基本作业时间Tab.1 Worktime of “Four shifts with two changing”

2 考虑用餐约束的乘务计划优化编制方法

2.1 DHM方法

DHM方法的主要思想是“替饭乘务员”在用餐之前或之后通过乘坐其他列车(作为旅客进行运输)到达/离开用餐点，即“随乘”。“随乘”示意图如图4所示。

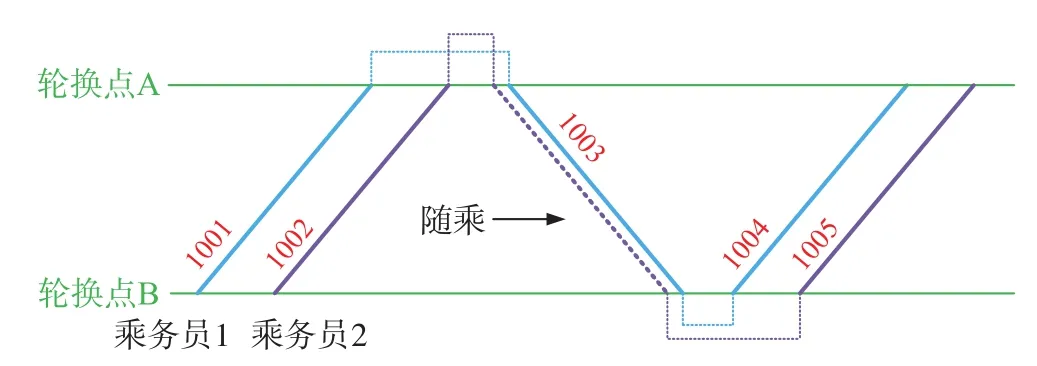
图4 “随乘”示意图Fig.4 Illustration of deadhead

乘务员1和乘务员2分别驾驶1001和1002次列车到达A点后，乘务员1下车进行短暂休息后继续驾驶1003次列车，而乘务员2则执行“随乘”任务搭乘1003次列车到达B点后继续执行驾驶1005次列车的任务。

DHM方法在航空领域应用非常广泛，而在轨道交通领域没有得到充分利用，仅对其进行了初步探讨。实际优化模型构建时，根据是否允许“随乘”，乘务计划实质上可以归纳为2类基础模型：集合覆盖模型(Set Covering Problem，SCP)和集合分割模型(Set Partition Problem，SPP)。DHM方法具体步骤如下。

（1）导入列车运行图(工作日、双休日)。

（2）根据线路的基本条件设置乘务驻点，并分别确定相关参数(最长连续驾驶时间、最短休息时间、最短用餐时间、出退勤)。

（3）构建“随乘”有向弧，并结合底图、任务段等构建时空网络图。

（4）根据基础参数设置所有节点的“随乘度”，其定义为任一点“随乘弧”进入的最小值，可以表示为

式中：R为时空图中不同时段车站的集合；U为可行任务号的集合；Ad为随乘弧的集合；为0-1变量，若有向弧(i，j)含在任务号u中，则= 1；否则= 0；Wi为节点i处“随乘度”的最小值。

（5）根据各任务段的状态(轮乘、交接班、就餐等)基于驻点最小间隔时间组合所有任务段(包括随乘弧)。

（6）调整任务号。例如，若有早高峰回库任务，则将其与晚高峰出库进行拼接。

（7）输出任务号。

2.2 VGM方法

实际编制过程中，由于部分轨道交通运营企业往往是以月或年为单位来均衡乘务员工作量。例如，某城市轨道交通线路规定乘务员月工作时间不得超过166.6 h，年工作时间不得超过2 000 h。以乘务轮转阶段为研究对象，提出VGM优化编制方法。

VGM方法的主要思想是将“替饭任务”、早高峰及晚高峰任务独立出一个班组，命名为“虚拟班”，虚拟班的最小人数可以表示为

式中：Nv为虚拟班的最小人数；Ni为高峰上线列车数；Na为基础班的最小人数为平峰时段的上线列车数。

由于运营企业的管理因素，每个班组的人数应相同，则每班所需最少人数为

VGM方法的轮转规则为日班、夜班、早班、峰班、休息。其中日班、夜班、早班的作息时间与传统“四班两转”相同，“峰班”则可能执行早高峰任务、送饭任务、晚高峰任务或休息任务中的任意一个任务。为了简化问题的复杂度，以工作日任务号为依据进行轮转计算。VGM方法编制方法示意图如图5所示。

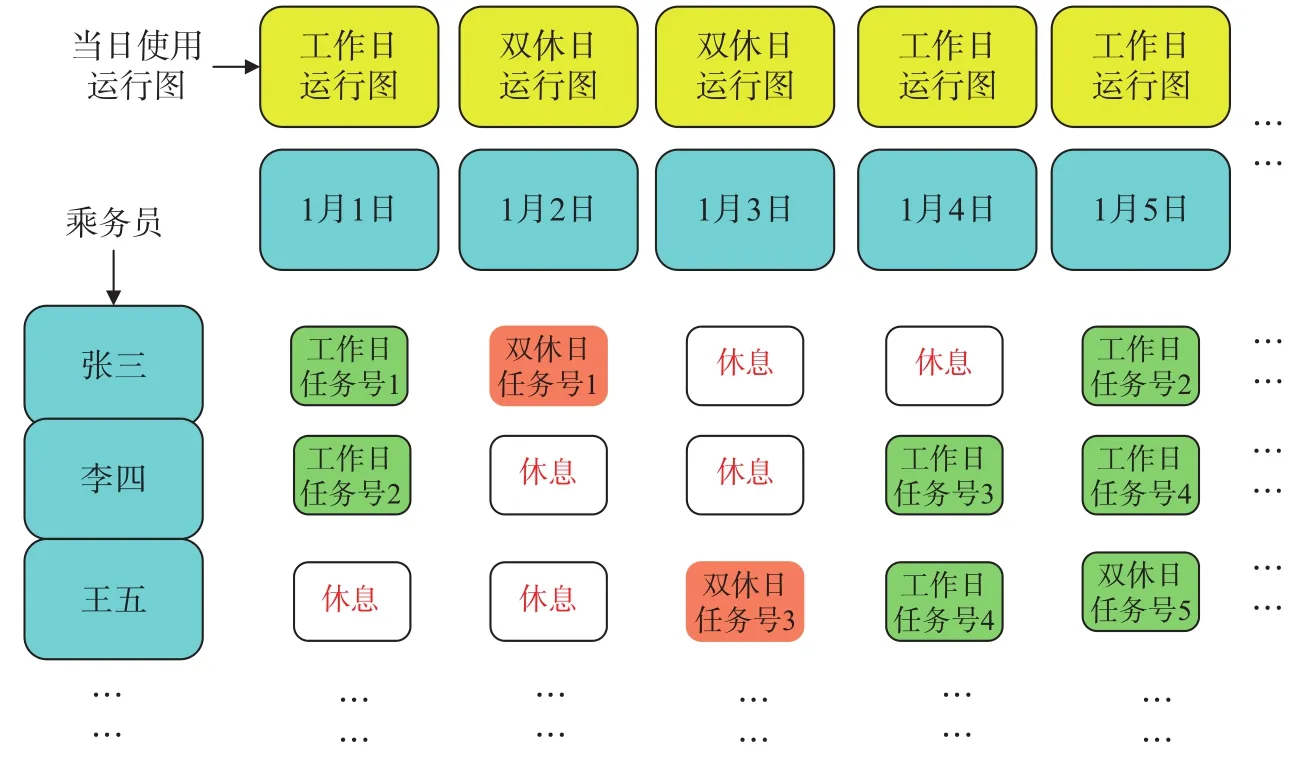
图5 VGM方法编制方法示意图Fig.5 Compiling with VGM method

VGM方法的优点是不仅保证了管理架构、组织的稳定，而且能够体现以任务为导向的灵活性进而提高乘务员的劳动生产率，其主要编制步骤如下。

（1）导入列车运行图(工作日、双休日)。

（2）根据各线路条件设置相关参数(轮转规则、月最少/最多驾驶公里数、员工培训安排等)。

（3）根据步骤（2）中设定的上、下班时间将任务号与早班/晚班/白班/峰班等进行一一对应。

（4）以工作日任务号为依据构建汉密尔顿回路模型，考虑到该问题为NP难问题，不存在多项式时间内的有效算法，因而采用贪婪算法进行求解。

（5）调整轮转任务。例如，若有员工请假、培训、临时身体不适等。

（6）输出轮乘规则。

2.3 特点分析

DHM方法和VGM方法是2类不同的乘务计划优化编制思路，均能达到均衡乘务员工作量的目标，但两者优缺点各有不同，具体分析如下。

（1）优化维度不同。DHM方法是以日为单位，以乘务计划任务号为研究目标，通过“随乘”的方法来优化乘务计划；而VGM方法则是以月为单位，通过设置“虚拟班”的方法来均衡工作量。

（2）编制难度不同。DHM方法在编制过程中需要加入“随乘弧”，无形中对乘务计划的编制加大了难度，同时也对乘务编制人员的业务水平提出了新要求。VGM方法则是在轮转阶段虚拟设置了“尖峰班”来填补运行图的不均衡性，相对难度较低。

（3）鲁棒性不同。在实际运营中调度员可能会进行一些临时的列车运行调整，这样会导致乘务计划在实际执行中出现“乱表”的现象。DHM方法由于任务号之间相对均衡，则仅需将2名乘务员之间的任务号进行对换即可；而VGM方法由于乘务员的工作量统计单位为“月”，且约束条件较多，调整难度较大。

（4）适用条件不同。DHM方法适用于：①线路之间必须存在换乘站，以便乘务员完成换乘任务；②乘务员出退勤地点必须统一，以避免乘务员超长的上下班通勤时间。VGM方法则适用于：①线路之间任务号数量较接近，以便“峰班”任务的分配；②乘务员培训、请假、年休制度的统一化管理。

3 结束语

随着我国城市轨道交通线路的不断增长、运营里程的不断提升，乘务计划的优化对于提升企业运营效率、降低运营成本具有重要意义。考虑用餐约束的城市轨道交通乘务计划编制优化研究，在考虑乘务员用餐的约束条件下，提出DHM和VGM 2种编制方法，探讨2种方法在多个“就餐点”及“网络线路乘务员共享”方法下的适用性和可行性。结合2种方法的不同特点，运营企业应基于实际应用场景进行综合抉择，以提高乘务员运用效率、增强精细化管理水平。为了进一步提高算法效率，未来的研究工作拟基于列生成算法的基本框架研究面向实际应用的编制方法。