基于OpenFOAM的水陆两栖飞机水面高速滑行研究

段旭鹏，孙卫平，魏猛，杨永,*

1.西北工业大学 航空学院，西安 710072 2.中航通用飞机有限责任公司，珠海 519040

水陆两栖飞机的水面高速滑行是力学现象十分复杂的过程，涉及到固、液、气三者的高速剧烈作用。飞机水上起飞较陆上起飞有很大不同，飞行员要在剧烈变化的水动力和高强度滑流作用下保持对飞机姿态和速度的有效控制，这对滑行安全性提出了更为苛刻的要求。

飞机水上起飞是一个动态过程，随着速度的增加，水线和水动力不断变化，气动力从无到有逐渐建立，要了解这一动态过程需要借助空气动力学、水动力学以及飞行力学等学科的相关理论知识。早期水上飞机除了要进行风洞试验以外，船体的设计还需要通过大量的水动试验进行评估。例如20世纪90年代问世的CL-215[1]水陆两栖灭火飞机，其船体尺寸和外形是通过一系列水池试验确定的。随着计算流体力学(CFD)技术的发展，研究者不断提高数值求解的精度，开始逐渐采用数值模拟方法，而减少试验的工作量。在过去的几年里，国际水池拖曳会议(ITTC)开展了很多船舶标模的阻力预测计算研讨会[2]。美国航空航天学会资助的阻力预测会议(DPW)致力于提高解算器的求解能力，使得CFD对跨声速气动问题的阻力计算精度不断得到改善[3]。现在，CFD技术已经具备了研究水上飞机相关问题的模拟能力。

两相流的数值研究虽然比较多，但是针对水陆两栖飞机的研究还不多见。上海交通大学的Qiu和Song[4]利用解耦式算法，基于商业软件开展了水陆两栖飞机起飞过程的动态模拟。该方法将气动力和水动力分开计算，有较高的计算效率，但是尚未考虑螺旋桨动力影响问题。飞机水上迫降与此类似，北京航空航天大学的Qu等[5]计算了支线客机的水上迫降问题，采用VOF(Volume Of Fluid)、6DOF(6 Degree Of Freedom)以及全局动网格技术研究了上单翼、高平尾飞机的水上迫降性能。

随着航空和航海技术的发展，对螺旋桨空气滑流和高速船体的水动力特性研究开展的都比较多，但是将这两方面内容耦合研究的工作也不多见。目前中国正在研制大型水陆两栖飞机，对于此类以涡桨为动力的大型飞机来说，如图1所示，水面滑行将产生大量的喷溅，随着速度的增加，喷溅基线不断后移，后机身周围产生涌起和凹陷，水动力矩随之变化，加上螺旋桨滑流的非定常作用，使得水上飞机的受力较陆基飞机更为复杂，设计和驾驶难度更大。要了解这一复杂流固耦合问题，需要对空气中的螺旋桨滑流和气水交界面同时研究。

数值研究上述问题，需要VOF方法、动网格技术、六自由度方程求解和螺旋桨滑流模拟等多项技术的耦合。由于两相流计算本身较为复杂，如果再直接模拟螺旋桨的非定常旋转，那么计算将付出高昂的代价。国外对螺旋桨理论的研究起步较早，早期的螺旋桨理论主要为动量理论和叶素理论[6-9]，随后基于上述理论方法国外学者提出了“激励盘”模型[10-11]。该模型具有方法简单、计算量少的特点，在一定的精度范围内可以替代3D实桨产生的滑流效应，同时可以大大简化用于模拟螺旋桨动态旋转的计算量。因此用激励盘模型来代替螺旋桨非定常计算的策略对于简化水陆两栖飞机的水面滑行问题来说是一个十分理想的选择。

图1 CL-215水陆两栖飞机水面高速滑行时刻照片Fig.1 Photograph of CL-215 amphibious aircraft taxiing at high speed on water

本文以OpenFOAM为平台，在两相流动态解算器内部加入激励盘模型，对两相流计算模块和激励盘方法进行了验证和确认，最后采用建立的方法研究了水陆两栖飞机水面高速滑行的非定常运动学与动力学特性。

1 数理模型和计算方法

1.1 两相流控制方程

VOF方法是一种自由面捕捉方法，其思想较为简单：每一个计算网格单元中都额外包含一项代表水的体积分数α，由初始气水交界面几何位置确定初值。位于交界面的网格单元既含有气体又有水，因此0<α<1；位于交界面之上的网格单元都是气体，因此α=0；位于交界面以下的网格单元都是水，因此α=1。在OpenFOAM中，牛顿流体不可压守恒形式的雷诺平均Navier-Stokes方程组为

(1)

(2)

式中：U为速度矢量；ρ为控制体内的流体密度；p为压力；g为重力加速度；μ为动力黏性系数；μt为湍流动力黏性系数。式(1)为质量守恒方程，式(2)为动量守恒方程。

VOF方法是在Navier-Stokes方程的基础上求解体积分数的，α随着速度场U运动的输运方程为

(3)

式中：α=Vwater/Vtotal，数值介于0和1之间，其中Vwater为水在单元内所占体积，Vtotal为单元总体积，因此流体空间内的密度和黏性可表示为

ρ=ρair(1-α)+ρwaterα

(4)

μ=μair(1-α)+μwaterα

(5)

式中：ρair和ρwater分别为空气和水的密度；μair和μwater分别为空气和水的动力黏性系数。

α函数在一个无限薄的界面上从1变成0，这就难以对α进行梯度的估计，进而导致气水交界面的数值耗散较大。为改善这个问题，OpenFOAM引入了一个虚拟压缩项，即加入一个虚拟速度场W，并使得W垂直于界面，保证了最终结果与原始方程保持一致。因此α输运方程的最终形式为

(6)

两相流的湍流模型方程形式与单项流完全相同，唯一需要注意的就是密度和黏性需要用式(4)和式(5)表示。

1.2 数值求解方法

interDyMFoam是不可压等温不混溶的非定常两相流解算器，附带可选择的网格运动和网格拓扑重构模块并耦合了6DOF方程的求解。对于本文研究的问题不对网格细化重构，只执行网格运动变形。解算器采用VOF方法计算每个控制体单元内的气、水所占组分，用以捕捉气水交界面即自由面。

用半隐式MULES(Multi-dimensional Universal Limiter with Explicit Solution)[12]方法求解含有体积分数α的方程式(3)。在非定常计算中尽量控制时间步长，因为时间步长越短，压力与速度的耦合越强，这是PISO(Pressure-Implicit with Splitting of Operators)[13]算法的典型特征。该算法具有较高的效率和精度，但是对网格质量较为敏感。压力与速度的耦合是通过传统的多重网格处理的，同时大量采用Rhie-Chow[14-15]插值方法，提高了PISO算法对各类网格的适应性。

时间导数项采用欧拉离散格式进行离散，传导项和耗散项的体积分通过高斯公式转换成面积分进行计算。在求解非定常自由面时，把动量方程中的传导项线性离散并加入限制器，体积分数方程的对流项采用van Leer格式进行计算。具体计算步骤如下：

1) 根据科朗数计算时间步长。

2) 求解网格运动方程，对网格进行变形。

3) 更新两相流运动参数，包括密度和黏性系数。

4) 采用MULES方法求解式(3)，得到体积分数。

5) 采用PISO算法求解速度和压力。

采用欠松弛迭代方法[16]来增加数值求解的稳定性以提高收敛性。对任意待求解变量，将新迭代得到的数值与上一步数值进行加权平均。其数学表达如式(7)，令β为迭代因子，有

φnew=βφnew+(1-β)φold

(7)

式中：φnew为新计算得到的结果；φold为上一步迭代的结果。

对于本文选择的k-ω湍流模型，其中的ω方程可以对整个壁面边界层进行积分，能更为方便地处理近壁面流场解算问题。解算器提供的壁面函数可以自动切换低雷诺数和高雷诺数求解方程，使得ω的解可以在黏性附面层和对数近壁面区域进行灵活适配[17]。

1.3 动网格方法

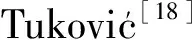
(8)

式中：γ为常数；u为网格变形速度。令xnew为新时刻网格坐标，xold为上一时刻网格坐标，Δt为时间步长，则有

xnew=xold+Δtu

(9)

1.4 6DOF方程

6DOF是指刚体六自由度运动，即任意给定刚体可以在三维空间沿3个转轴平移和滚转自由运动，称之为六自由度运动。图2显示了刚体6个自由度的轴系和运动形式，其中X、Y、Z表示在笛卡儿坐标系中沿3个坐标轴的平动，θX、θY、θZ表示绕3个坐标轴的转动。求解动网格方程之前，需要通过求解1.1节中的控制方程得到流场结果，随后利用流场结果对刚体各物面进行积分可得到刚体的受力以及对质心的力矩，其具体表达式为

图2 6DOF轴系和运动形式Fig.2 Axis and movement form of 6DOF

(10)

(11)

式中：Fflow和Mflow为流场对物面的作用力和力矩；Fext和Mext为重力和其他外力及其作用力矩，对于本文的研究对象来说，Fext包括螺旋桨拉力和升降舵偏转带来的平尾附加压力。在两相流动态求解过程中，利用松耦合形式引入人工虚拟质量项来对Navier-Stokes方程与六自由度方程进行联合求解。

1.5 激励盘的添加

对于以涡桨为动力的水陆两栖飞机来说，飞机起飞时螺旋桨滑流对飞机动力学影响不可忽视。现有商业软件、开源软件中的VOF方法，无论是显式、半显式半隐式或者全隐式的时间推进格式，其时间步长都很小，计算效率都不高，而且计算量比较大。如果再对螺旋桨进行非定常模拟，计算耗时几乎无法接受。

本文选用的激励盘模型是在螺旋桨桨盘区域定义一个具有一定厚度的扁平圆盘，在圆盘边界包络的计算网格内添加体积力源项，通过修改解算器中的控制方程以达到向流场注入动量的目的。Svenning[19]对较早版本的OpenFOAM单相流解算器进行了激励盘的添加，本文将在其工作的基础上，将激励盘模型加入到OpenFOAM 2.3.1中的动态两相流解算器。主要改进包括：激励盘的空间位置从一次性计算改为随飞机刚性实时运动；体积力从固定不变改为实时更新，以适应动态计算问题。动量的添加是通过添加体积力源项实现的，体积力的分布按照复杂程度可以分为均匀、非均匀以及基于螺旋桨性能分析的多种形式。为平衡精度与算法复杂度，本文采取Goldstein[20]的非均匀分布：

(12)

(13)

(14)

式中：fbX和fbθ分别为轴向和切向体积力；r为激励盘中某个确定点的径向坐标；RP为桨盘外径；RH为桨盘内径；AX和Aθ为常数。令Δ为激励盘的厚度，则AX和Aθ的表达式为

(15)

(16)

(17)

其中:T为拉力；Q为扭矩。根据式(12)～式(16)，在已知螺旋桨旋转产生的拉力T和扭矩Q的情况下，就可以得到桨盘沿轴向和切向的体积力fbX和fbθ的分布。此时，修改动量方程式(2)，以源项的形式将体积力fbX和fbθ添加到方程右端，式(2)就变成式(17)所示的新的动量方程。此时按照1.1节和1.2节介绍的方程和方法即可求得滑流作用下的流场结果。

2 算法的验证与确认

在进行水陆两栖飞机水面高速滑行的数值模拟之前，应首先对算法的气动力和水动力计算模块进行耦合验证。受到设备条件的限制，水池拖曳试验尚无法对气动力进行准确测量。因此本文将采用气/水动力分别考核的思路来对算法进行验证。具体来说，是采用Wigley水池拖曳试验和螺旋桨单桨风洞试验的数据结果对新开发的动态激励盘两相流方法分别进行水动力和气动力方面的验证和确认。

2.1 Wigley水池拖曳标模计算

在船舶领域，Wigley标模外形简单有丰富的试验数据[21]，是考核水面航行体计算有效性的典型算例。该标模有3种船体截面形状：抛物线型、直线型、矩形，船体长宽比也有不同参数。本文选取长宽比为10的抛物线型船体为研究对象，如图3所示。模型方程如式(18)所示，参数见表1。

(18)

采用笛卡儿网格对计算域离散，并对水面加密。中等网格的船体面网格最小尺度为40 mm，即1%L，首层附面层厚度为3.3 mm，对应的y+值约为200，膨胀比率为1.3，如图3所示。在此基础上，为了进行网格收敛性研究，还生成了另外两套密度不同的网格，3套网格的体单元数目分别为：80万、120万、360万。计算使用的弗洛德数表达式为

(19)

式中：V为航行体运动速度;g重力加速度的大小。

计算时Fr=0.267，雷诺数Re=6.66×106，湍流模型为SST(Shear Stress Transport)。对3套不同密度、不同y+的网格进行了计算，得到的结果如表2所示。试验得到的CD=0.004 16，虽然y+=60的加密网格计算精度最高，但是当y+达到200，壁面网格增长率低于1.3以后，结果精度随网格量的增加将变得不明显。3套网格对自由面的捕捉精度较好，相比于试验结果，差异主要在于船艏处的波高，如图4所示。基于上述结果可以得出，y+越小结果越准确，然而与单相流气动力计算有所不同，水动力计算的y+达到200后，就能得到较为理想的结果。

图3 Wigley计算网格和结果波形Fig.3 Computational grid and wave result of Wigley hull

表1 Wigley船体模型参数Table 1 Parameters of Wigley hull model

表2 Wigley计算网格收敛性Table 2 Computational grid convergence of Wigley hull

图4 Wigley船身波形(Fr=0.267，Re=6.66×106)Fig.4 Wave profile on Wigley hull (Fr=0.267，Re=6.66×106)

2.2 两相流激励盘模型验证

大型水陆两栖飞机在国内FL12风洞进行了螺旋桨单桨测力试验，本节采用试验数据结合非定常计算的数值模拟结果对激励盘模型进行验证。如图5所示，FL12风洞是4 m×3 m闭口回流式低速风洞，试验模型为1∶15的六叶单桨和短舱的组合构型，动力模块采用电机驱动，使用机械天平测定拉力系数。试验的来流风速为40 m/s，模型迎角和侧滑角均为0°，螺旋桨桨叶角为31°，转速为10 000 r/min。

图5 单桨测力低速风洞试验现场照片Fig.5 Photograph of single propeller force measurement in low speed wind tunnel

首先通过非定常单桨计算对试验状态进行复现，目的是得到足够丰富的流场数据用以验证激励盘的计算能力。这里采用滑移动网格技术模拟桨盘转动，湍流模型为SST，非定常时间步长采用桨盘旋转3.6°所用时间dt=6×10-5s。非定常单桨计算得到的拉力系数Tc为0.059 5，比试验结果小10%。

体积力的添加不影响计算的复杂度，在耦合激励盘的两相流非定常计算过程中，时间推进步长仅仅受到VOF方法限制，对于水上飞机的高速滑行问题来说，通常是在10-3s量级。相对而言，螺旋桨旋转的非定常模拟需要采用更为复杂的动网格方法，比如重叠网格、滑移网格，即便采用非惯性系简化方法，对时间步长的选择都有严格的限制。对于本文研究的问题来说，如果计算3D实桨的旋转，时间步长一般在10-5s量级。因此激励盘的选用从时间成本上来看，可以使计算保持较为经济的运行方式，具有较强的工程实用价值。

激励盘的验证计算采用了3套不同密度的网格，网格节点数分别为稀疏网格64万，中等网格200万，细化网格620万。以非定常计算得到的拉力和扭矩作为输入进行计算，结果如图6所示：截取流场中心剖面观察马赫数(Ma)云图，3D实桨与激励盘二者的计算结果总体上是相似的，流场经过桨盘加速流动，形成包裹发房的一束高速射流，即“滑流”。细微的差别在于，前者在绕过发房的头部边界层内有小范围速度减缓，随着气流的行进滑流边界开始变得模糊，滑流区域开始向中心收缩；与此相对，后者滑流强度较为均匀，边界更为清晰平直。此外为进行定量对比，在图6(a)的坐标系下，在桨盘中心后方3倍半径处，从发房表面沿气流垂向向上分别截取线段分析速度型,如图6(c)所示，其中Z/R是以桨盘半径R无量纲化得到的流场内的位置高度。3套 网格的结果差异较小，说明激励盘计算对空间离散精度要求不高。激励盘滑流束状直径略小，其马赫数峰值较非定常结果小0.01，这对复杂的全机两相流非定常计算来说是可以接受的。

图6 激励盘与3D实桨非定常模拟结果对比Fig.6 Comparison between simulation results of actuator disk and unsteady computation of 3D propeller

3 水上飞机两相流数值模拟结果及分析

国内外学者对螺旋桨滑流现象以及滑流和地效的耦合问题已经做了较为深入的研究，对水面高速航行体的研究也取得了较为丰富的成果[22-24]。本节将基于对以上成果的研究认识，尝试进一步探索在滑流、地效、自由面三者的共同作用下，飞机高速滑行的非定常运动过程。利用经过验证的动态激励盘两相流算法进行高速滑行数值模拟，本节首先给出非定常计算的时间历程，然后分析该阶段滑流、拉力、平尾控制力对全机运动学和动力学特性的影响，最后给出自由面受到扰动之后的典型特征。

3.1 水上飞机的计算网格

在不影响主要研究目标的情况下，对飞机外形进行了简化，去掉了浮筒、发房和起落架舱等部件。计算网格仍然采用对水面适应性较好的笛卡儿网格。虽然结构网格同样具有流向延展性的特点，但是受物面网格拓扑的影响，在机身近水面附近的网格延伸方向往往会被迫改变，导致自由面计算的误差增加。幸运的是，笛卡儿网格一方面可以严格按照水平方向进行各向异性的网格加密，另一方面在水面与物面相交处，它具有非结构网格的特点，可以灵活对物面进行贴合，而不改变自由面的网格拓扑方向。

水上起飞水动力占据了合力的大部分比重，水动力的模拟至关重要，因此除了机翼前缘等部位还特别对船体表面和周围近场空间进行加密，如图7所示。为提高激励盘模拟精度还在虚拟桨盘所在位置进行了加密。对于本算例，相同首层高度网格对应的水动力与气动力的y+恰好相差10倍，结合2.1节Wigley标模研究结论，水下y+取100是可行的。因此全机物面边界层首层高度统一设为0.1 mm，对应的气动力y+为10，水动力y+为100，总网格量为800万。

图7 水陆两栖飞机计算网格Fig.7 Computational grid of amphibious aircraft

3.2 飞机水面滑行的非定常计算历程

飞机水上起飞过程分为两个阶段，排水运动阶段和断阶滑行阶段。飞机启动后，受螺旋桨拉力作用开始低速航行，船体的断阶绕流造成底部压力降低和流动分离，使得飞机受到向下的“吸”力，飞机下沉水线上升。随着速度的增加，水下流动分离范围逐渐增加，负压达到极值，飞机下沉至最低点，阻力达到峰值即“阻力峰”。利用螺旋桨的剩余拉力飞机通过阻力峰继续加速，气动力开始逐渐起作用，飞机受气动升力和水动升力共同作用克服重力不断抬升，断阶后部开始进入空气，飞机从双断阶滑水逐渐过渡为单断阶滑行，当气动升力增加到与重力相等时飞机离水完成起飞。

本文聚焦起飞过程中的断阶滑行阶段。飞机在断阶滑行过程中物理机制涉及3个领域，包括空气动力学、水动力学和飞行力学。对于断阶滑行阶段，飞机的动态稳定性至关重要，受稳定性边界影响，必须对飞机加以控制才能避免进入“海豚跳”[25]的危险状况。对于这种复杂过程的非定常数值计算来说，则需要考虑平尾的控制力，才能避免大幅振荡从而得到稳定的计算结果。如图8所示，除了螺旋桨滑流以外，飞机的滑行还需要在螺旋桨拉力和升降舵附加力的共同作用下达到平衡。这两种外力的添加是通过修改OpenFOAM六自由度动态计算函数，添加刚体外力模块实现的。相对于模拟真实的升降舵偏转，该方法进一步提高了计算效率。因此，本节的非定常计算过程是首先利用Navier-Stokes方程耦合VOF和激励盘方法求解两相流问题获得飞机的气动力和水动力，然后通过添加的刚体外力模块施加螺旋桨拉力和升降舵附加力，最后将物面受到的流体作用力和刚体外力一起代入到飞行力学6DOF方程进行计算，即可得到飞机滑行的运动特性。

非定常计算历程如图9所示，图中Zcoord为自由液面的Z坐标即自由面高度，Zcoord=0表面液面未受扰动，t为时间，AOA为迎角。计算速度设定为40 m/s，给定4°初始迎角，在螺旋桨滑流、拉力和平尾附加力的共同作用下，经过15 s物理时间飞机稳定在5.5°～5.8°之间，重心高度较静浮状态升高约1.28 m。全机阻力建立得较快，5 s时间即达到稳定，阻力系数约为0.45，注意这是全机阻力，包括气动阻力和量值较大的水动阻力。总阻力与全机重力之比约为0.16。根据迎角变化历程曲线，选择3个俯仰最为剧烈的典型时刻观察飞机姿态和流场情况。首先可以明显看到流线通过激励盘以后的收缩和旋转，其次断阶排开水形成喷溅自由面，自由面高度随迎角增加而增加。t1时刻迎角为7.5°时的液面最大高度可达0.45 m，t2时刻迎角为4.5°时的液面最大高度为0.33 m。随着计算时间的推移，飞机纵摇幅值逐渐减小趋于收敛，最终在t3时刻达到稳定(俯仰振荡幅值不超过2°[25])。此时的平尾附加下压力为8 000 N，等效偏角约为-18°。

图8 水陆两栖飞机外力示意图Fig.8 Sketch of external forces of amphibious aircraft

图10显示了稳定滑行时的滑流速度剖面，来流马赫数为0.12，经过加速后最大可达0.28。在桨盘后等距切出若干剖面，观察流过机翼和襟翼的滑流形状，可以看到在激励盘所在区域流场得到加速，加速区域为圆环形状，这与真实桨盘的效果相同。顺航向在内、外发房中心位置分别截取两个剖面。观察外侧剖面的流线，可以更加明显地看到，由于桨盘的加速作用，流管出现明显的收缩，随后受机翼和增升装置影响，滑流在机翼前后缘产生明显的上洗和下洗，最后沿自由面流向后方。

图9 水陆两栖飞机滑行计算历程Fig.9 Computation history of amphibious aircraft during taxiing

图10 滑流剖面的速度分布和流线形状Fig.10 Velocity field distribution and slipstream at a certain slice

3.3 滑流与动力影响分析

目前除了俄罗斯的Be200以外，大部分水上飞机都是以涡桨为动力的，这是因为水上飞机更加注重低速飞行性能，更重要的是利用涡桨的低速大拉力特点可以更快地起飞离水以提高安全性。螺旋桨滑流对水上起飞性能的影响较大，在设计中必须加以考虑。本节通过3个状态有无滑流和动力的对比研究，尝试揭示螺旋桨对水上起飞动态过程的影响规律。

3个状态分别为：CC(Clean Case)—无动力无滑流、SO(Slipstream Only)—无动力有滑流、SF(Slipstream & Forces)—有动力有滑流并附加平尾操纵力。来流速度为40 m/s，采用与3.1节相同的网格，计算得到的运动学和动力学参数时间历程如图11、图12所示。

图11中右侧纵轴为飞机重心升沉变化(CG(Center of Gravity) rise)。从图中可知，与无动力无滑流状态CC相比，滑流产生一个较大的低头力矩，使得状态SO的迎角降低约2.5°。分析图12曲线，左侧纵轴为气动力升力系数(AerodynamicCL)，右侧纵轴为气动阻力系数(AerodynamicCD)和总阻力系数(TotalCD)，通过能量的注入，升力系数大幅增加,从1增加到1.8，但是由于没有平尾的附加控制，结合图11，飞机的低头抵消了升力系数的增加，使得飞机的重心没有明显的抬升。观察图12的阻力系数曲线，以右侧纵轴为刻度，可以看到，飞机总阻力明显高于气动阻力，说明尽管飞机处于断阶滑水状态，浸润面积已经很小，但是由于水的密度和黏性远远大于空气，水阻力仍然占据相当高的比重。对比气动阻力发现，高速滑流流过机翼时，大幅提高了压差阻力使得气动阻力系数增加。然而气水动总阻力没有显著变化，是因为飞机低头降低了水面滑行的水阻力，气动力阻力的增加与水动力阻力的减小使得总阻力基本不变。

图11 滑流影响下的飞机俯仰和重心升沉变化历程Fig.11 History of aircraft trim angle and rise of center of gravity under effect of slipstream

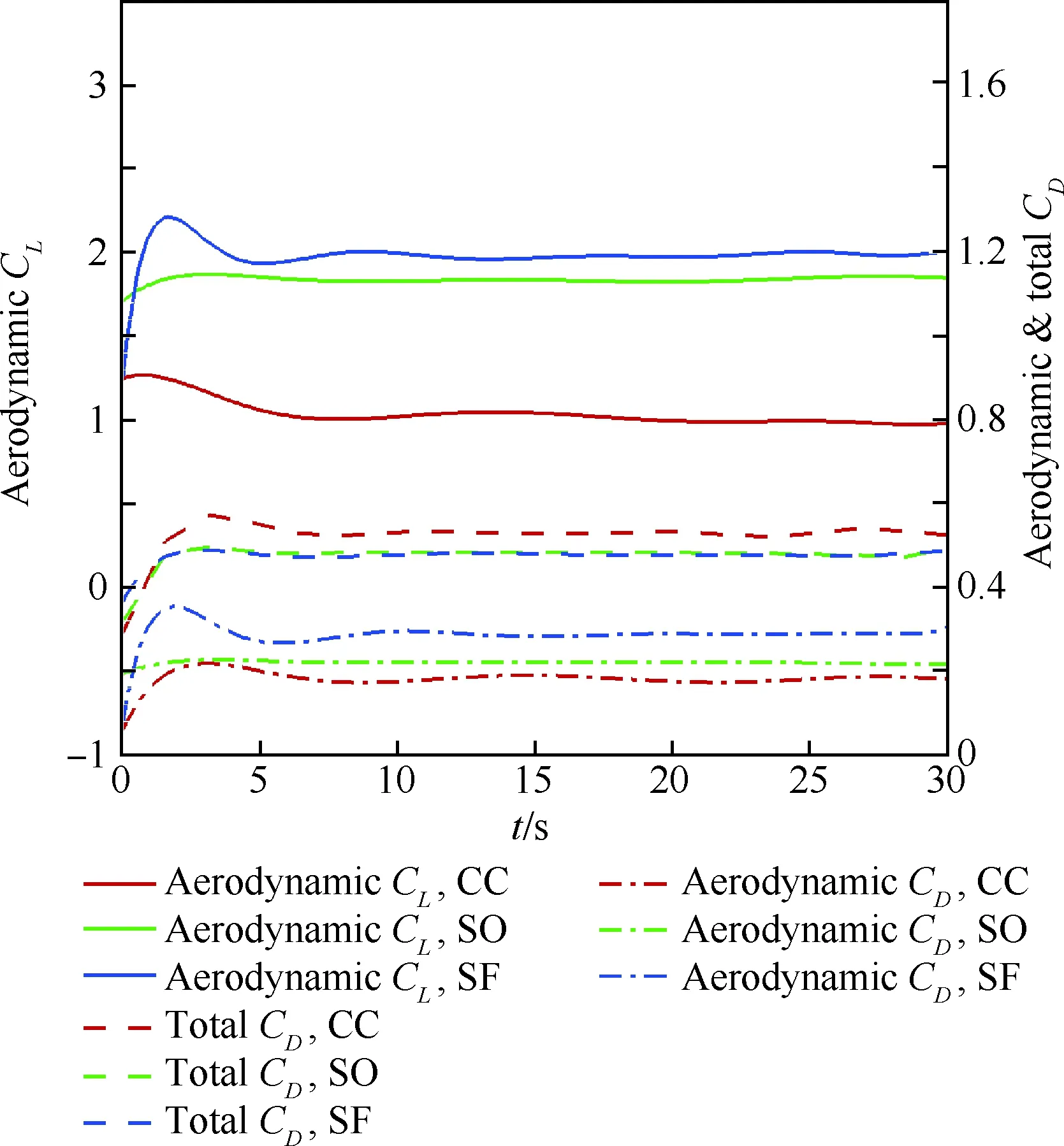
图12 滑流影响下的飞机气动力和总阻力变化历程Fig.12 History of aircraft aerodynamic forces and total drag under effect of slipstream

为尽量模拟真实起飞状态，添加了螺旋桨的轴向拉力，由于水陆两栖飞机采用位置较高的上单翼布局，拉力线高于重心高度，因此不可避免地会进一步增加飞机的低头力矩。为此，必须对飞机进行控制才能保证高速滑行过程中飞机能够保持一个合理的姿态。通过添加刚体随体力模拟升降舵上偏18°的效果，此即状态SF。观察图11的蓝色曲线，飞机迎角回到理想的5.8°左右，纵摇幅值变小，变得更加稳定。图12显示，迎角的增加使得对滑流的利用更为有效，蓝色的气动升力系数显著增加到2左右，如此高的升力系数得益于滑流和地效的共同作用，这比无滑流和地效状态提高了接近一倍。飞机重心平稳提升，浸润面积减小，水动阻力降低，总阻力系数随之减小到0.5左右。正是由于迎角的增加，气动阻力与单独滑流作用的状态相比是有所增加的。

表3显示了3种状态的航态和气动力比重的对比数据。在螺旋桨滑流的单独作用下，飞机明显低头，加上平尾控制力后，迎角增大，气动升力占比从34%提高到77%，在滑流附加升力的作用下飞机进一步抬升，导致水阻力降低。这说明把迎角控制得尽量高，而不超出稳定性上边界对飞机的水面高速滑行是十分有利的。显而易见，滑流产生的附加阻力会使得气动力阻力占比有一定的增加。

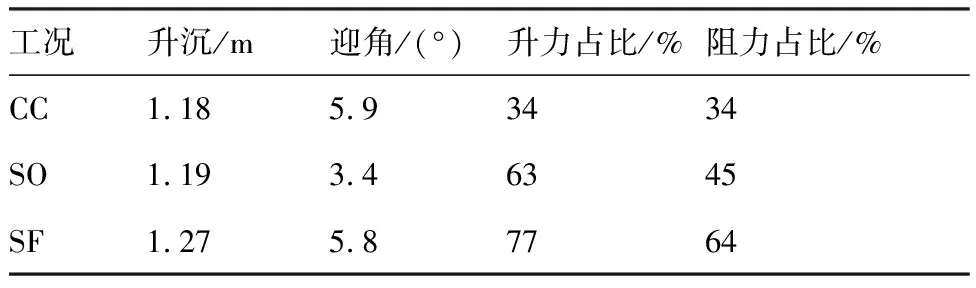
表3 飞机水面滑行V=40 m/s的航态和气动力比重对比

3.4 飞机高速滑行时的自由面结构

船体设计的一个主要目的是，使飞机有一个较为宽泛的稳定滑行迎角范围，从图11中可以看到，在3°～8°范围内飞机均可稳定滑行。断阶位置、高度和断阶后的船底后缘角这3个参数的综合设计影响到单断阶滑行特性。从图13中可以看到迎角为5.8°时，断阶两侧可以观察到明显的涌起，高度约为0.4 m，涌起形成后向飞机侧后方流动。断阶脱出的自由面凹陷较深，使得后机身底部与水面还有较大空间，有利于后体的船底避免来自断阶的水流冲刷而造成阻力的增大。如果仔细观察图9可以看到，自由面形状受滑行速度和滑行面迎角影响较大，迎角越大自由面涌起和凹陷的高度越大。结合图9和图13可知，在机身尾部，水面凹陷达到最深并开始逐渐恢复。从机翼后方的自由面来看，螺旋桨滑流尽管经过襟翼有强烈下洗，但由于水的密度是空气密度的1 000倍，除了受网格密度影响而无法模拟的飞沫和细丝等雾化结构以外，滑流对水面主体形状的影响是十分微小的。其次船体设计还要尽量减小水面冲击载荷，以降低结构重量。如图13(b)所示，40 m/s的速度已接近离水速度，此时的水面冲击压力可达174 kPa(计算参考压力为标准大气压，即100 kPa)。

此外，船体设计对喷溅特性的要求也很高，要求在高速滑行、转弯以及波浪水面等各种滑行工况下，喷溅区域尽量避开螺旋桨、襟翼、尾翼等空气动力学控制部件。与光滑粒子流体动力学(SPH)方法相比，VOF方法的重点在于模拟流体的力学特性，对自由面细微结构捕捉能力是不足的。但是，当自由液面区域的空间离散达到一定规模后，其自由面的主要结构也是可以在一定程度上体现出来的。从本例的自由液面形状来看，如图14所示，基本的喷溅结构已经模拟出来，可以清晰看到断阶前受舭弯抑制而改变流向的须状喷溅和断阶后涌起的主喷溅。

图13 稳定滑行时自由面形状和船体压力分布(AOA=5.8°)Fig.13 Free surface and distribution of pressure at hull during stable taxiing (AOA=5.8°)

图14 稳定滑行时的喷溅结构Fig.14 Spray structure during stable taxiing

3.5 螺旋桨滑流和地面效应对高升力系统的影响

为了进一步分析螺旋桨滑流和地面效应二者对高升力系统的影响，还在单项流不可压解算器simpleFoam中添加了激励盘模型，并专门进行了无滑流无地效、无滑流有地效、滑流地效同时作用的3种状态计算对比。模型迎角统一采用3.3节真实高速滑行状态的计算结果5.8°，来流速度和地面高度同样与该状态相同。网格依然采用3.1节介绍的笛卡儿网格，与前述计算不同的是本节用滑移壁面代替了自由面。

过内侧发动机中心做一个平行于对称面的纵向剖面，图15显示了3种状态的速度场和襟翼上表面流线，并用来流速度对速度场进行无量纲化，即以U/Uinlet表征无量纲速度。当关闭发动机时，在地面效应的单独作用下(图15(b))机翼上表面的速度场基本不变；然而机翼的下表面出现速度阻滞，其流速有一定程度的降低；襟翼上表面流速略微增加，进而绕襟翼流动的分离区相应减小。无地效状态(图15(a))之所以会出现襟翼分离区是因为飞机还没达到起飞速度，气流动压较低，襟翼后缘的逆压梯度较大。打开发动机并耦合地面效应(图15(c))可以看到，机翼上表面流速显著增加，襟翼上表面尾缘区域形成高速附着流；机翼下表面形成了一条由低速气流和高速气流组成的复合气流通道；此时襟翼在高速附着流的作用下，其上表面气流分离区完全消失。

图16显示了剖面与机翼、襟翼交线上的压力系数(Cp)分布对比,图中X/c为无量纲弦向位置。关闭发动机的状态下，地面效应对机翼上表面的影响只在前缘增加了吸力峰，而下表面受到气流速度阻滞的影响，由伯努利方程可知该区域的压力就会增大，图中蓝色下半部曲线也证实了这一点。可以看到压力的增加沿弦向一直持续到襟翼缝道底部，使气流加速进入襟翼缝道，进而使得襟翼上表面的附面层能量得到补充，使分离得到了抑制。在发动机和地面效应同时开启状态下，机翼和襟翼上表面吸力沿弦向均匀增加，这是因为水上飞机的发动机安装位置较高，使得滑流大部分从高升力系统的上方通过，更好地将滑流的流向速度转化为更多升力以帮助飞机尽快离水。同时观察黑色曲线的下半部，可以看到在压力表面，机翼和襟翼前缘正压力峰值明显，这得益于机翼下方复合气流通道的一部分贡献。观察速度场，正是在机翼和襟翼的前缘下方存在两个流速最低的区域，所以再次由伯努利定律可知相应位置的压力才会显著增加。除此以外，与文献[26]的研究结果类似，襟翼前缘这部分正压力将会更加明显地对缝道内的气流加速，气流绕襟翼头部的圆弧流动将形成柯恩达效应，从而进一步抑制襟翼上表面气流分离。因此，可以说水上飞机水面高速滑行时地面效应和螺旋桨滑流的耦合使得机翼高升力系统的升力特性得到了显著的提升。

图15 距离对称面5 m处过内侧发动机中心的剖面速度分布和襟翼上表面流线Fig.15 Profile of velocity distribution across center of inner engine at the distance of 5 m to symmetry plane and streamlines over suction surface of flaps

图16 3种状态的机翼和襟翼压力系数对比Fig.16 Comparison of pressure coefficient distribution over the wing and flap in 3 cases

4 结 论

1) 本文基于开源CFD软件OpenFOAM发展的动态激励盘两相流计算方法可大幅降低计算复杂度，减少计算量，可应用于以涡桨为动力的两栖飞机水面高速滑行模拟。

2) 计算结果显示，当水陆两栖飞机达到单断阶高速滑行时，并不是像陆地起飞一样平稳，而是会伴有小幅的俯仰和升沉振荡。

3) 滑流在滑行中的作用明显，显著增加气动升力和低头力矩，因此需要增加升降舵的控制力才能更好地将姿态控制在较为稳定的范围。在稳定性边界范围内，尽量提高滑行迎角对飞机的快速离水是十分有利的。

4) 断阶这一水陆两栖飞机特有的设计特点，不仅可以在高速滑行过程中减小水动阻力还可为飞机的纵向操纵提供更大的可用空间。

5) 水上飞机水面高速滑行时地面效应和螺旋桨滑流的耦合使得机翼高升力系统的升力特性得到了显著的提升。