民用飞机气动外形数值优化设计面临的挑战与展望

周铸，黄江涛,*，高正红，黄勇，陈作斌，余婧

1.中国空气动力研究与发展中心 计算空气动力研究所，绵阳 621000 2.西北工业大学 航空学院，西安 710072

迄今为止，数值优化设计技术在飞行器气动外形综合设计中发挥了重要作用。数值优化具有自动化程度高，多目标寻优能力强，很大程度上克服了“Cut and Try”传统人工修型方法的不足，实际应用中开始受到设计人员的青睐，是国内外知名空气动力学研究机构一个重要的研究方向。例如密歇根大学Martins教授的MDO团队[1-2]，斯坦福大学Jameson团队[3]，德国宇航院基于非结构化求解器TAU[4]，以及法宇航基于CFD代码elsA均发展了气动外形优化设计体系[5-6]。国内在数值综合优化设计也做了系列研究工作，一定程度上推广应用于型号设计[7-11]。

气动外形优化设计体系的发展主要集中在两个方向上：梯度类优化与非梯度类优化，两者各有各自的优缺点，在实际应用中可以互相结合充分利用自身的优势；在面临的基础科学问题上，两者表现不同，前者面临的主要问题是局部性限制以及多目标设计问题，后者主要面临的是大规模设计变量与高维多目标优化问题，但在软件体系中两类方法的基本要素相同。系统总结、梳理优化设计体系各个要素的基础科学问题、关键技术以及实际工程应用的需求，对发展先进、高效率优化设计软件，把握气动设计技术的发展方向具有重要意义。

飞行器数值优化设计大体是按以下步骤来进行的：首先对设计对象进行参数化，即选取合适的设计变量，然后确定需要优化的目标，建立合理的优化数学模型，再用一定的优化方法进行优化设计，直至达到设计要求。设计变量、目标函数和优化算法是优化设计过程中的3个基本要素。

对现代民用飞机而言，其安全性、舒适性、经济性、环保性的需求反映到设计过程中，除了追求多点多目标的气动性能最优外，还需考虑气动/结构、气动/噪声的一体化设计问题，是典型的多目标、多学科优化(MDO)设计问题，同时设计结果的质量和可靠性也对数值优化设计技术提出了更高要求。

本文首先系统总结了气动外形优化设计平台中的各个主要环节，对各个环节常用方法的优缺点及其面临主要问题进行梳理，给出了建议与解决思路，提炼了工程设计对设计体系的基本要求，并对多学科设计的未来发展方向以及需要解决的问题进行了展望，希望能够对促进设计空气动力学与MDO技术的发展提供有价值的参考。

1 气动外形数值优化体系的基本要素

1.1 学科分析模块

毋庸置疑，在民用飞机气动外形数值优化体系中，各个学科的分析手段是保证设计过程、结果鲁棒性、可靠性的最基本环节。优化体系对学科分析模块最基本的要求是高精度、高可信度、高效率，然而这几个基本要求之间往往是相互矛盾的。

民用飞机气动外形综合数值优化所涉及的学科分析手段通常包含计算流体力学、计算固体力学以及流固耦合技术。

这3个技术手段中，以计算流体力学的运算量最为庞大，是数值优化设计中面临的一大瓶颈，为此，研究人员提出了变可信度、代理模型多种手段、方法来缓解该问题。最常用的气动特性分析方法包含了面元法、全速势方程、欧拉方程结合边界层修正、Navier-Stokes方程等，不同的分析方法被用于不同的设计阶段；面向不同的设计对象，优化体系对CFD的要求也不尽相同，例如，对于传统气动设计，全湍流数值模拟本身就可以发挥主要作用，对于层流减阻类气动设计，优化体系对边界层转捩数值模拟精度提出了要求。尽管优化体系中高可信度CFD技术已经发挥着不可替代的作用，CFD数值技术仍然在一些领域显得力不从心，比如失速特性的改进，传统雷诺平均Navier-Stokes方程可信度大大降低，虽然DES、LES等先进湍流数值模拟技术计算可信度大幅提高，但应用于优化设计依然成本过高。不仅如此，由于结构化、非结构化求解器效率、内存需求的差异，在对求解器类型选择上，同样有着种种限制，例如，基于进化算法的优化体系对求解器的选择偏向于结构化，基于非结构求解器的进化优化形式，目前来看计算资源还不能完全胜任，而对于伴随方法的优化体系来讲，两种类型的求解器都是不错的选择。

相对于计算流体力学，计算固体力学的运算代价明显要低一个量级，但不可回避的是，随着计算机的发展，气动、结构大规模设计变量优化开始发挥作用，有限元分析的计算效率也将迎来挑战。在气动结构综合设计中，对于结构有限元数值分析结果，优化体系关心的是结构变形、应力、重量等参数，一般将重量作为目标，冯·米塞斯应力以及结构变形作为约束条件来处理，而这些参数的分析、决策与飞行器空气动力学特性紧密相关，流固耦合技术在这个环节上扮演了重要角色。

在精细化设计中，流固耦合技术面临的主要问题包含了流固耦合界面高精度插值、大规模数据传递、大型稀疏矩阵运算等方面，这些方面是保证物理场变量守恒、计算效率的关键环节，同时也是超大规模设计变量下、气动结构一体化设计不可回避的基础科学问题。

1.2 参数化建模

参数化建模方法是实现外形自动化设计变形的前提，正因为如此，在气动优化领域，科研人员在气动外形参数化方面投入了大量的研究，从简单的曲线参数化到全机复杂外形一体化参数化，每一次参数化方法的进步，都将设计对象的复杂程度、优化体系的设计能力向前推进一步。以剖面设计参数化为例，从经典的Hincks-Henne函数[12-13]与基于类函数/型函数CST[14-15]的翼型设计，到结合线性插值将典型截面参数化向机翼、机身、短舱的参数化推广，参数化建模在向工程应用迈出了实质性的一步，如图1所示，图中相关表达式的详细含义可以参考文献[14]。

图1 CST方法在不同类型外形中的应用[14]Fig.1 Application of CST method in different types of shape[14]

曲面类型的参数化建模，以NURBS、Bezier曲面[16-18]为典型代表，该类方法以其强大的曲面建模能力，在飞行器整流包(见图2)[19]、机翼设计中也发挥了重要作用[20]，但在基于离散数据参数化的前提下，存在节点矢量选取依赖于CFD网格分布、总体参数化能力弱等问题。

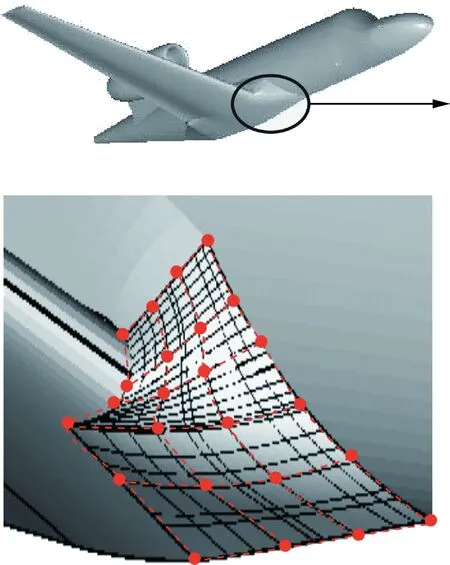
图2 运输机整流包参数化[19]Fig.2 Parameterization of transport aircraft fairing[19]

尽管曲线参数化方法结合线性插值技术、Bezier、NURBS曲面在三维气动外形参数化上取得实质性成果，但对于复杂外形的参数化方面依然力不从心。由于优化设计体系中，往往采用的是离散点数据作为物面输入，且需要物面输入与网格重构进行匹配使用，曲线参数化方法结合线性插值技术以及直接Bezier、NURBS曲面在复杂拓扑网格情况下的通用性面临难题。

随着计算机图形学的发展，交叉学科的优势在参数化方面开始体现出来，最有代表性的是自由变形技术(FFD)的提出[21]，该方法极大程度上拓展了基于网格离散点形式的参数化范围，并从最基本以Bernstein基函数的FFD技术迅速向NURBS为基函数的NFFD技术、扩展型FFD技术(EFFD)、多块FFD技术方向发展[22-23]，进一步充实了该方法的应用能力，图3～图5给出了FFD方法在部件、全机构型参数化方面的应用范例。

由于该方法主要原理是将物体嵌入弹性框架内实现弹性域属性下的自由变形，因此，从很大程度上消除了复杂外形带来的网格拓扑、部件组合难处理等问题。另一方面，由于该方法对所属域内的任意坐标的可操作性以及逻辑不变性，也可以用来进行网格变形，如图5所示。

图3 机翼部件参数化Fig.3 Parameterization of wing

图4 全机一体化参数化[23]Fig.4 Parameterization of the whole aircraft[23]

图5 FFD方法应用于变形网格Fig.5 Application of FFD method in grid deformation

参数化方法目前需要解决的问题是特殊部件的兼容性与独立性要求。例如，内、外型面的约束限制以及不同部件参数化建模方法的独立性主要体现在：外流型面进行参数化变形时，必须保证与内流型面保持一定的容积约束，避免曲面相交、容积减小等问题；唇口/进气道参数化变形时，必须保证与外流型面做到保形一致，且要考虑唇口平行法则以及内部曲面精细化描述，这对参数化建模来讲是一个技术挑战。

不同部件参数化建模方法的兼容性要求主要体现在：内、外型面变形后的外形数据结果能够做到统一处理，保证部件之间原有的连续性、光滑性等特征；数据结果能够做到统一处理，为高效的网格重构提供有效的物面信息输入。

1.3 网格重构技术

利用高可信度CFD技术以及结构有限元分析进行气动、结构性能评估时，空间网格重构技术是一个非常重要且具有挑战性的环节。在优化体系中，网格重构的鲁棒性、计算效率以及质量直接决定了设计平台的设计效率、设计品质以及设计能力。

针对不同的问题研究人员发展了不同的变形网格方法，对于结构网格包括径向基函数法、无限插值方法、有限元方法、弹性体方法以及四元数方法等[24-31]；非结构网格最常用的动网格技术包含径向基函数、弹簧法[32]、有限元方法、四元数方法以及弹性体方法，这些方法已经应用于许多领域，新型、改进型动网格方法也在不断发展中。对于不同优化设计问题，对变形网格的要求也不尽相同，布局形式优化对网格变形的基本要求是强鲁棒性，局部精细化设计对变形网格的要求是高质量，一体化设计则对两个方面均有较高要求。表1、表2给出了常用于气动优化的几种变形网格的适用性与总体评价。

目前来看，结构网格求解器方面，对于多块网格，单纯TFI技术只能进行局部小变形优化，而RBF-TFI技术拓展了对多块网格的变形能力，在气动设计中发挥着主要作用。非结构网格求解器方面，弹簧法等传统方法在气动设计领域也发挥了很大作用，近年来提出的子空间径向基函数RBF方法[33]具有较高的计算效率以及结构、非结构网格通用性等特点，也开始在设计领域发挥作用，是一个值得关注的研究方向。图6～图10给出了适用于气动设计的不同变形网格方法的应用与对比。

表1 几种变形网格方法的适用性Table 1 Applicability of several grid deformation methods

表2 变形网格的综合性能评价

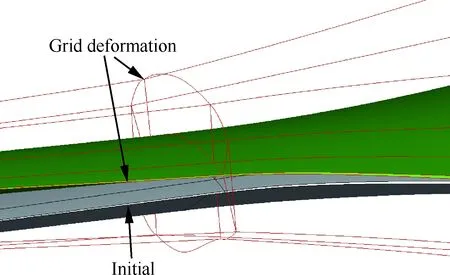
图6 RBF_TFI变形网格技术Fig.6 RBF_TFI grid deformation technique

图7 四元数变形网格技术[28]Fig.7 Quaternion grid deformation technique[28]

图8 子空间RBF变形应用于结构网格Fig.8 Application of subspace RBF method in structured grid

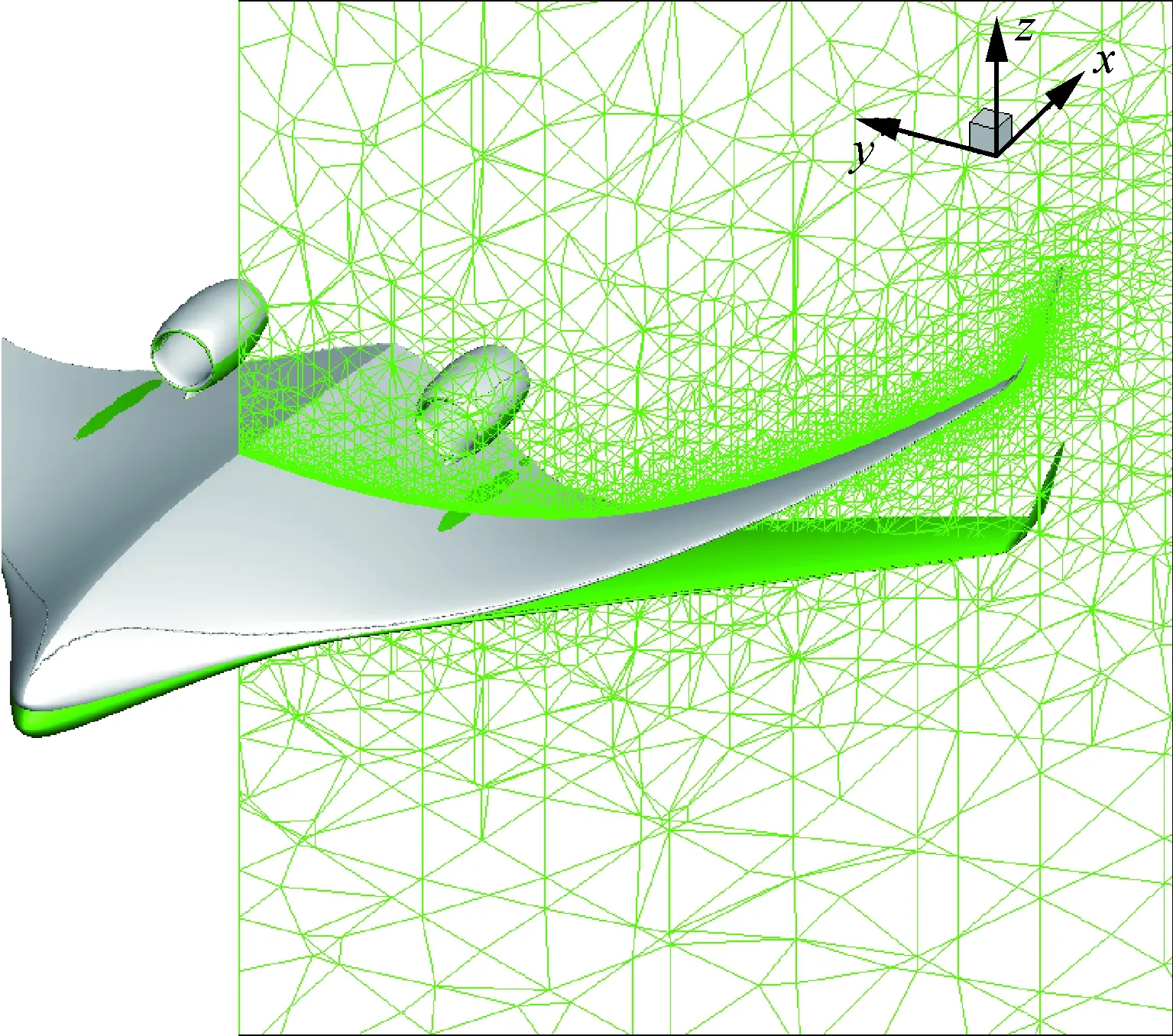
图9 子空间RBF变形应用于非结构网格Fig.9 Application of subspace RBF method in unstructured grid

图10 子空间RBF变形应用于非结构网格(局部视图)Fig.10 Application of subspace RBF method in structured grid (partial view)

1.4 最优化算法/约束处理

气动优化体系中主要有基于梯度的优化算法，以及基于非梯度信息的优化算法两种，工程中需要针对不同的设计问题进行合理的算法选择。

梯度类算法需要在计算目标函数对设计变量的梯度(或叫灵敏度)基础上，外形根据梯度信息来改变寻优。最常用的梯度类算法有最速下降法、牛顿法、共轭梯度法以及序列二次规划(SQP)法[34-36]，梯度类算法的核心是获取准确的导数信息以及合理的下降步长，收敛速度较快。最速下降方法编程简单，工作量小，但在极值点附近存在收敛慢，跳动现象等问题；牛顿法利用二次函数作为近似目标函数，将指向近似二次函数的极小值方向作为下降方向，在极小值附近的收敛性很好，收敛速度快，而且具有二次终止性和二阶收敛速度，但存在初始点选择依赖性，矩阵计算量大等问题，为克服该问题研究人员又进一步提出了拟牛顿方法；共轭梯度方法将与二次函数矩阵有关的共轭方向作为下降方向，收敛速度优于最速下降方法，由于不需要矩阵求逆运算，所需内存较小。梯度类算法对目标空间有着强烈的数学特性要求，无法跳出局部最优的缺点，且计算效率很大程度上依赖于梯度信息的获取方法，比如传统的复变量方法和有限差分法。然而对于飞行器气动外形精细化设计来讲，优化问题包含了成千上万个设计变量，此时，传统的梯度计算手段可行性大大下降。基于伴随思想的导数计算以其与设计变量无关的优势，结合梯度类算法，近年来在气动设计上发挥着重要作用，是今后值得关注的研究方向。

非梯度类算法不需要计算梯度信息，它是从一个点的群体开始搜索寻优，利用概率转移规则，而非确定性规则，这种全场搜索理论上讲可以得到全场最优。非梯度类算法典型代表是模拟退火算法、遗传算法、粒子群算法和免疫算法等进化类算法[37-39]，进化算法在工程优化中应用最多的是遗传算法与粒子群算法，前者是模拟生物进化机制的原理，后者是模拟鸟群、鱼群的觅食行为。相比较于梯度类算法，该类算法具有全局最优性、处理复杂问题等优势，尤其在多目标优化设计中，能够给出更为丰富的解集，供设计人员选择。但存在随机性，随着输入、输出的增加计算量庞大等问题。比如，在气动设计中，进化算法能够给出较好的优化结果，但对于大规模设计变量问题存在种群规模庞大，计算量倍增，工程应用可行性变差等问题，尽管很多研究人员对进化算法做了大量改进测试，但这仍是进化算法目前面临的一个最大技术瓶颈，该缺点严重阻碍了进化算法优化技术在实际工程中的应用。

总的来讲，无论是气动外形综合优化还是其他学科的优化问题，寻优效率和质量在一定程度上都是一对矛盾，如何能够充分利用各个算法的优点是数值优化向工程应用推广的关键。

优化设计中最常用的约束处理方法主要有外罚函数法、内点法和乘子法[40-41]，最常用的乘子法基本思想是从基本问题的拉格朗日函数出发，结合适当的罚函数，从而将原问题转化为无约束优化问题。乘子法常用于SQP优化中，也是基于离散伴随体系的气动设计中最常用的方法。在智能进化算法中，约束的处理方式较为灵活，应用最为广泛的是罚函数方法，即利用罚函数将综合性能差的个体在进化过程中被淘汰；在计算资源充沛，计算效率较高的情况下，种群规模允许较为庞大，也可以直接采用直接剔除的方式进行个体淘汰。设计人员可以视情况采用灵活的处理方式，基本原则是要保证种群多样性。

1.5 灵敏度分析方法

灵敏度分析是气动设计中设计变量分层协同优化、主分量识别的主要技术途径，同时也是基于梯度信息的优化体系的一个重要环节。飞行器优化体系中，根据学科对象的需求，可以将灵敏度分析归结为两类：学科灵敏度分析与系统灵敏度分析。

学科灵敏度分析主要包含了手动求导、有限差分、符号微分、复变量方法、解析方法、自动微分以及伴随方法[42-45]，各个方法均有自己的优点和不足。对于优化体系来讲，主要关心的是方法的效率与精度。目前来看，复变量方法与自动微分是较为受关注的方法，其中复变量方法在求解一阶导数时比差分法更准确、效率更高，但存在二阶灵敏度导数步长敏感性问题。自动微分方法具有前向与后向两种模式，其中前向模式的计算量与输入变量(设计变量)成正比，反向模式计算量与输出变量(目标)成正比，高维设计变量问题中计算效率相较于前向模式大大提高，但存在内存需求大的问题。

系统灵敏度分析的主要任务是研究系统级设计变量对系统性能的影响。学科级灵敏度分析手段在向系统级拓展时，由于庞大的数据需求以及交叉学科之间的相互影响，显得力不从心。不同学者提出了不同的研究方法，最常用的办法是将整个系统分解为不同的子系统。对于不同的系统分解思路，对应不同的系统灵敏度分析方法，比如可用于层次系统分析的最优灵敏度分析，适用于耦合系统的全局灵敏度分析以及适用于混合分解系统的延迟耦合伴随系统。

最优灵敏度分析着重研究输出变量与输入变量对问题参数的敏感性，具有逻辑关系简单，计算量小，同时也可以应用于单学科系统；全局灵敏度分析能够将子系统的灵敏度与大系统的分析联系起来，其核心是联立求解线性方程组，为多学科优化设计提供耦合灵敏度信息，例如，式(1)给出了气动结构耦合系统的线性方程组[1]：

(1)

通过求解式(1)可以获取耦合灵敏度信息。同样，从式(1)也可以看出，全局灵敏度尽管大大减少了系统分析的次数，但其计算量仍然与设计变量的个数成正比，在大规模设计变量问题上仍然力不从心。

为解决该问题,Martins提出了耦合伴随方法，即对耦合系统进行变分，构造耦合伴随方程，从而进行耦合灵敏度分析。进一步提出了延迟耦合伴随方法，将两个学科的伴随系统独立求解、伴随变量延迟处理，克服了耦合伴随系统求解困难、内存需求大等问题，该方法与直接耦合系统不同，计算量与设计变量个数无关，仅仅与目标函数个数相关。并成功应用于超声速商用飞机多学科设计，如图11所示[1]。

图11 基于耦合伴随系统的气动结构优化[1]Fig.11 Aero-structural optimization based on coupled adjoint system[1]

1.6 代理模型技术

结合高保真CFD软件和智能优化算法开展气动外形优化，大多采用代理模型来减小庞大的计算开销。这类方法通常称为基于代理模型的优化(Surrogate-Based Optimization, SBO)，文献[46-47]对这类方法给出了比较系统的综述。由于方法相对简单、气动分析可靠、优化过程健壮、工程应用灵活，波音公司采用这种方法开发了一种使用高阶分析代码的多学科设计优化系统MDOPT[48]。国内研究和应用这类方法的文献远多于基于梯度的优化方法。近年来应用上一些有代表性的工作，包括：文献[49]结合随机权重粒子群优化算法、Kriging代理模型和对应的期望改善(EI)函数加点准则进行加样本点以及代理模型重建，进行了考虑螺旋桨滑流影响的机翼气动优化设计；文献[50]基于自适应取样Kriging模型和多种群协作粒子群算法开展了跨声速层流翼身组合体稳健性设计；文献[51]采用分群粒子群算法以及误差反向传播训练算法神经网络模型，对某型客机融合式翼梢小翼的后掠角、倾斜角和高度等参数进行了稳健型气动优化设计；文献[52]对小展弦比薄机翼，采用Kriging代理模型和粒子群算法进行了多目标的约束减阻优化设计，跨、超声速多设计点的阻力特性显著改善；文献[53]针对发动机吊舱外形采用混合遗传算法和Kriging响应面模型进行优化；文献[54]对若干风力机翼型进行了多约束多目标的实用优化设计。

SBO本质上是通过构造近似数学模型(即代理模型)，将复杂的学科分析从优化进程中分离出来，而将便于计算的近似模型耦合到优化算法中，多次优化迭代循环后得到实际问题的近似最优解。代理模型利用已知点的响应信息来预测未知点的响应值，目前大致有数据拟合模型、降阶模型(如基于正规正交分解的POD模型)以及启发式模型(或称多可信度、变可信度、变复杂度模型)3类。数据拟合模型的研究与应用较多，如气动优化领域广泛采用的Kriging模型，其他还有多项式响应面模型(Polynomial Response Surface Method, PRSM)[55]、Co-kriging模型[56]、径向基函数、BP神经网络(Backpropogation Neural Net, BPNN)、RBF神经网络、支持向量机(Support Vector Regression, SVR)模型[57-62]等。Kriging模型对确定性问题适应性好，但对大设计空间问题的适应性较差；BP神经网络对强非线性大设计空间问题的适应性较好、方便重复使用，缺点是计算量较大；基于SVR的代理模型在小样本情况下具有较好的泛化能力。

发展代理模型主要围绕如何提高非样本点预测精度和增大设计变量数量规模两个问题开展。国内的学者在代理模型预测精度以及增大设计变量数量方面开展了大量的研究，尤其在Kriging代理模型方面做了大量研究工作，其中文献[63]对Kriging模型做了较为全面的综述与总结，展望了Kriging方法与代理优化算法未来的发展趋势。提高非样本点预测精度希望采用尽量少的样本量获得预测精度更高的代理模型，有静态和动态改进两类办法:①静态改进方法，包括针对具体问题比较上述模型做出选择、利用拉丁超立方设计、正交设计、均匀设计等试验设计(DoE)方法确定建模样本等。有在构建代理模型上做工作的，如文献[64]对高低保真度分析预测结果之间的差值，利用代理模型的方法进行建模，用差值代理模型对低保真度分析的误差进行修正，提高其预测精度。它对两组数量不同、独立的高、低保真度数据分别建立Kriging模型，进而通过Co-Kriging方法构建高、低保真度模型之间的关系模型，充分利用低保真度分析信息来提高代理模型整体的预测精度，在保证预测精度的前提下，提高了构造代理模型的效率。另一思路如文献[65]，通过集成Kriging插值型代理模型和BP神经网络回归型代理模型，构造双层代理模型，在同样样本的条件下，取得更高的预测精度。这里第1层模型用回归型模型，它对数据样本的整体分布可进行较好地拟合，第2层模型则用插值型模型，对第1层代理模型的预测误差进行建模，优化时用来修正第1层代理模型的预测，这种做法比单独使用插值型模型精度有所提高。②动态改进的方法，不要求优化使用之前构建的代理模型非常准确，而是在寻优过程中不断改善样本完善模型，在提高代理模型精度的同时得到最优解。这类方法应用较多，被称为自适应取样，实质是寻优过程中加点策略。文献[66]使用了两类建模样本加点准则：一是根据代理模型预测的非样本点均方差添加样本点的期望改善准则；二是假定代理模型全局准确，仅加入当前找到的最优点来局部改善模型的最小化预测(Minimizing the Predictor, MP)准则。精细化的优化问题如翼型的反设计问题和AIAA ADODG(Aerodynamic Design Optimization Discussion Group)的第一个基准测试问题(NACA0012的跨声速无黏减阻优化问题)，对建立的SBO方法可能是一项较难的测试。文献[67]在解决后一个问题时引入了“多轮优化策略”，在寻优过程中除采用上述方法改进代理模型外，还需要在每一轮优化中重新调整设计空间，再完善模型，这也可视为一种动态改进方法。

增大设计变量的数量规模对构建代理模型是项挑战。随设计变量增多，建模需要的样本规模迅速增大，以至于难以构建满足精度要求的代理模型。文献[68]应用系统分解思想，基于响应均值灵敏度的概念，提出了对大规模的设计变量进行重要性分组的策略，对分组的设计变量进行分层协同优化，这降低了系统的复杂度，可沿用以往的代理模型方法。在文献[69]中可以看到设计变量超过40以后，Kriging模型的预测精度迅速下降，构建代理模型需要的样本点数也迅速增加，出现“维数灾难”问题；针对56个设计变量控制的BWB构型，用原来的粒子群算法和Kriging模型优化，会出现“精度冻结”的现象，而采用多个物理分区的协同优化策略，则可以克服该现象在这种高维优化问题中得到满意的结果。文献[70]直面高维代理模型的构建问题，采用高维模型表示方法(High Dimensional Model Representation, HDMR)构建SVR代理模型，针对70个设计变量控制的翼身组合体构型和50个设计变量控制的战斗机机翼气动优化问题，与基于拉丁超立方采样构建的SVR代理模型相比，模型预测精度显著改善。HDMR方法的基本思想是：大多数物理系统中只有相对低阶的输入变量相关项才对输出响应有重要影响，可以利用该特性对物理系统分层级来表示，即由相互正交的每层级的组分函数组合而成。对每个组分函数进行低维的插值或回归建立代理模型，再经组合就可形成高维的代理模型。此外，文献[64]提出由于高、低保真度分析的预测精度与设计变量的多少和设计空间的大小没有必然联系，在任何设计空间中，两种分析预测结果差值的大小和变化始终远小于物理量本身的值和变化，对这种差值构建模型所需的样本量大小不会随着设计空间维数的增加超线性增长，这样在优化中直接使用低消耗的低保真度分析和差值代理模型，就可进行大规模设计变量的高保真度优化。

代理模型以上问题的研究可能还会持续，在气动结构综合优化、健壮优化[71-74]中的应用逐渐增多，满足多学科多目标优化和不确定度分析与传递需要的代理模型可能是今后的一些发展方向。

1.7 目标函数

目标函数与约束处理是优化体系中决定最优解/解集的关键环节，在设计空间一定的情况下，目标函数和约束条件直接决定了系统的极值分布特性、可行域范围等，从而决定了设计结果。

现阶段，目标函数的定义一定程度上依赖于研究人员对问题的认知程度以及设计经验。然而在多目标优化设计中，当目标数增多至≥3时，加权平均的可行性变差，Pareto最优前沿面的维数随之增加，非劣解集数目将会呈指数级增长，这将大大增加算法的时间和空间复杂度。与此同时，当目标函数的维度达到一定数量时，几乎所有个体都是非支配解，由此大大削弱了基于Pareto支配进行排序与选择的效果；另一方面，优秀个体在进化过程中不一定能被保存下来，导致整个算法的搜索进程收敛困难。需要指出的是，随着优化目标的增加，可视化水平降低，设计人员难以对优化结果进一步决策选择。

目前，解决高维多目标优化问题的主要途径包含3个方面[75]：

1) 改进优化算法，使其更适宜于高维优化问题，通过定义宽松的Pareto占优机制，增大种群中个体间的选择压力，从而加快算法的收敛，然而这些改进在工程应用中是否有普适性，还是个值得研究的问题，即便能够得出最优解集，一方面计算量过大，另一方面优化结果难以显示，进一步决策相当困难。

2) 引入数学分析中的降维思想，将高维多目标优化问题进行主导能力分析，在不失问题主特征的前提下，提取决定问题本质的主要分量，将冗余目标剔除、或者转化为约束条件，将高维多目标优化转化为低维优化问题。可以预见，该类方法对于实际工程复杂问题具有重大的理论意义和工程应用价值，该类方法的降维设计主要应用于模式识别、信号和图象处理、控制理论和其他领域中[76-78]，而在飞行器多目标优化设计中的应用研究较少，文献[23,75]论述了基于主分量分析降维算法在气动外形多目标、多学科优化中的可行性，如图12所示。

3) 加权系数平均方法，利用静态或动态加权系数对设计目标进行综合评估，将问题转化为单目标优化问题。该方法对小于3个目标的优化设计有一定的可行性，但对于高维问题来讲可行性较差，主要原因在于权系数选择的困难。因此，多目标优化问题一直是近年来优化设计领域研究的热点。

图12 PCA目标空间降维前后收敛历程[23]Fig.12 Convergence history of PCA target space before and after dimension reduction[23]

1.8 不确定性优化设计技术

在飞机设计、生产、使用过程中，都不同程度地包含着不确定性。由于使用的数学物理模型及其求解方法存在局限，离散流场空间的计算网格分辨率不够等问题，CFD模拟分析预测的气动特性存在一定的不确定度性；飞行器真实飞行过程中速度、高度、姿态与构型几何加工误差，也存在一定的不确定性。传统的优化设计方法没能很好地考虑这些随机因素，导致设计结果对随机扰动可能变得敏感，一旦出现偏离设计点，飞机的性能就会下降甚至恶化[79]。解决这些实际问题要求发展不确定性优化设计(Uncertainty-Based Design Optimization, UBDO)[80-81]技术，主要解决不确定性影响下的优化设计问题，获得最优决策/结论/设计的同时综合提高设计方案的稳健性和可靠性。它分为稳健设计优化(Robust Design Optimization, RDO)和可靠性设计优化(Reliability-Based Design Optimization, RBDO)，前者主要降低系统性能对不确定性影响的敏感度；后者对设计方案满足约束的可靠度进行考虑。通常RDO适合于表示稳健性和系统性能之间的折衷解决方案，为多目标优化问题，处理方法包括加权求和法[82]、折中法[83]、基于偏好的规划法[84]等。而RBDO需要在各种不确定性来源下满足特定风险和目标可靠性[85]，常采用基于一次可靠度分析方法(FORM)的可靠性指标法(Reliability-Index-Nased Approach, RIA)和观测性能方法(Performance-Measure Approach, PMA)[86]来处理该问题。上述方法一般仅考虑低阶矩信息度量，忽略了偏度与峰度等高阶矩信息；另一项不足是大多仅适用于单一优化目标，但实际工程问题中可能存在多个相互耦合、冲突的优化目标，需要在优化过程中一并考虑。

美国NASA Langley中心对基于不确定性的方法(Uncertainty-Based Methods, UBM)[87]进行了调研，强调应用改进的计算与实验方法解决飞行器多学科设计问题的必要性，其中重要内容之一是UBDO，可归结为一个双层嵌套问题，内层为不确定性分析，外层是对设计变量的寻优。不确定性分析目前主要形成了5类方法：第1类是蒙特卡罗仿真(Monte Carlo Simulation, MCS)[88]方法，这类方法以蒙特卡罗打靶为基础，属无偏估计，计算成本高；第2类是摄动方法(Perturbation Methods)[89]，它将一个随机函数在其均值附近展开成Taylor级数，取前一阶或二阶展开，固有缺陷是不确定性放大时误差较大，只适合小尺度的随机输入问题；第3类是基于矩估计的方法[90]，有一次二阶矩方法(First Order Second Moment Method，FOSM)、一次可靠度分析方法(First Order Reliability Method，FORM)、二次可靠度分析方法(Second Order Reliability Method，SORM)等[91-93]；第4类是多项式混沌展开(Polynomial Chaos Expansion, PCE)方法[94]，其基本思想是将精确解在随机参数空间进行多项式展开，如果精确解对于随机参数有良好的正则性，该方法指数级收敛，但求解联立方程组较为困难；第5类比较流行的方法是随机配置(Stochastic Collocation, SC)[95]法，通过融合MCS方法与多项式Galerkin投影方法的优势，基于一些特殊的样本点来构造高精度的多项式逼近。上述方法一般适用于不确定性维数不大的情况，精度/效率对样本点的选取较为敏感，亟需研究有效的多维混合不确定性分析方法。

2 工程应用对优化体系的基本要求

飞行器气动外形综合优化技术在实际工程应用中，必须具备灵活处理设计问题、满足不同设计需求以及决策方便等能力，这就对优化体系建设提出了要求，这些要求与软件设计框架与设计基础科学问题紧密相关。

1) 定义模块化

各个子功能模块化定义对灵活处理不同设计问题来讲意义重大，在此基础之上，面向不同的设计问题，可以用简单的流程组合方式进行优化链的构建，简化前处理过程，该项工作的一项核心是标准化输入输出接口。著名的优化软件Isight、ModeFrontier等均采用了这种思路。图13给出了本课题组软件的模块化分类。

2) 有效的阶段性设计分析手段

气动外形设计面临的工程问题是初步选型设计阶段与精细化设计阶段，基础科学问题是大规模设计变量与高维度目标空间，如何有效地对设计空间进行管理是提高设计效率的关键。一般来讲，最有效的方式是基于高低可信度分析工具进行阶段性设计，利用低可信度学科分析工具进行快速初步设计，缩小设计空间，进一步利用高可信度工具进行精细设计。

对于大规模设计变量问题，可以采用两种方式进行分层处理，一方面，基于不同灵敏度分析结果对大规模设计变量分层处理，进行分层优化，降低复杂程度。但该技术一定程度上忽略了设计变量之间的相关性。另一方面，可以利用伴随方法的设计变量无关性，实现初始外形的选型，进一步利用非支配解进行多目标优化，既克服了大规模设计变量问题，减小了设计空间，又避免了加权平均多目标优化的不足，但存在初始点局部性问题。例如，图14给出基于全速势方程快速优化设计，该算例不带挂架短舱，以初步设计结果为基础，基于高可信度CFD技术进行小设计空间内非支配解全机优化设计。初始设计外形带短舱设计后尽管会改变压力分布形态，但仍然可以大大缩小设计空间，有效利用阶段设计手段的优势。

图13 优化软件模块化框架Fig.13 Framework of modularization for optimization software

3) 较高的多目标、多学科优化的可视化水平

从未来发展看，无论是民用飞机还是作战飞机的气动设计，对综合性能的要求均越来越高，因此，设计目标呈现高维趋势，此时，目标函数的可视化直接影响了设计人员的有效决策，如何利用数据资源、改进多目标算法对目标空间进行有效的分析、处理是优化体系需要进一步关注的内容。图15给出了基于主分量分析方法下目标降维的过程，这种方法一定程度上解决了高维多目标优化决策问题。

4) 设计效率-评估模块、硬件设备

设计效率是衡量设计体系优劣的一个重要方面，其影响因素是多方面的，比如管理框架、最优化算法收敛性、学科分析效率、硬件设备等，其中管理框架、最优化算法收敛性、学科分析效率可以通过软件体系的算法架构进行优化改善。硬件设备方面一直是设计空气动力学需要加强的环节，与计算空气动力学不同，设计空气动力学对个体的分析需要成千上万次甚至更大的计算量，比如基于进化方法的大规模设计变量优化问题、高维多目标优化问题，对种群个数的要求极高，这些问题上，现有代理模型表现的力不从心，即使采用分层优化，计算量仍然可观。在工程设计效率要求下，基于伴随方法在处理大规模网格条件的精细化问题时，也需要高性能集群作为支撑，来完成多点优化设计。世界著名的空气动力学研究机构，诸如NASA、DLR、斯坦福大学等，均在基于高性能计算的数值优化上投入了大量的财力、物力。

图14 基于全速势方程的快速优化Fig.14 Fast optimization based on full potential equation

图15 基于主分量分析的多目标优化Fig.15 Multi-objective optimization based on principal component analysis

5) 设计理念、经验与优化系统的耦合

从目前优化设计体系、计算能力等方面的综合发展来看，人工设计理念、设计经验仍然起到关键作用，例如“人在回路”思想[96]就体现了设计理念、经验在优化过程中的主动积极的反馈作用。先验的流动机理认知、设计经验等方面与优化系统耦合，能够很大程度上提高优化体系的设计效率与作用。设计经验与优化体系耦合主要体现在对目标函数的定义、几何约束的处理以及对流动形态(如压力分布形态)的约束等方面，尤其是目标函数的定义，较大程度上决定了极值分布特性直接影响设计结果，而机理认知、设计经验能够为目标函数定义提供积极的指导。随着大数据挖掘、深度学习等关键科学问题的研究发展，未来可以为优化系统提供更为可靠的数据支撑，提高优化体系的决策能力。现阶段，加强先验的流动认知、设计经验等与优化系统的耦合是提高设计效率的有效手段。

3 民用飞机气动综合设计值得关注的技术与发展方向

从上述总结分析可以看出，民用飞机气动外形数值综合优化未来的发展是精细化设计与多学科一体化设计，这两个方向面临计算量庞大、近似模型数学建模精度低、耦合灵敏度分析困难等问题。而近年来基于伴随方法的设计技术是当前的一个研究热点，尤其是耦合伴随系统，受到国内外研究人员的关注，为精细化设计、多学科一体化设计提供了有效手段。中国空气动力研究与发展中心立足自主研发，在该系列方向开展了大量的系列性研究。

3.1 基于流场伴随方程的优化设计

对于气动优化设计的最小化问题[97]：

(2)

式中：I为目标函数；W为流场守恒量；X为设计变量。考虑残差约束R(W,X)=0，引入伴随算子Λ。可得目标函数表达式为

L=I+ΛTR

(3)

(4)

式(4)即流场伴随方程，求解Λ之后，进行目标函数梯度信息快速求解。

(5)

(6)

式中：ΔX表示设计变量梯度。

图16、图17给出了全机构型网格分布与基于离散伴随方法的梯度验证[79]，图18、图19给出了CRM标模的参数化与离散伴随气动设计，仅10次优化，完全消除了激波，充分说明了伴随方法的高效性。

图16 宽体飞机全机表面网格[79]Fig.16 Wide-body aircraft surface grid[79]

图17 全机构型梯度验证[79]Fig.17 Full-aircraft gradient verification[79]

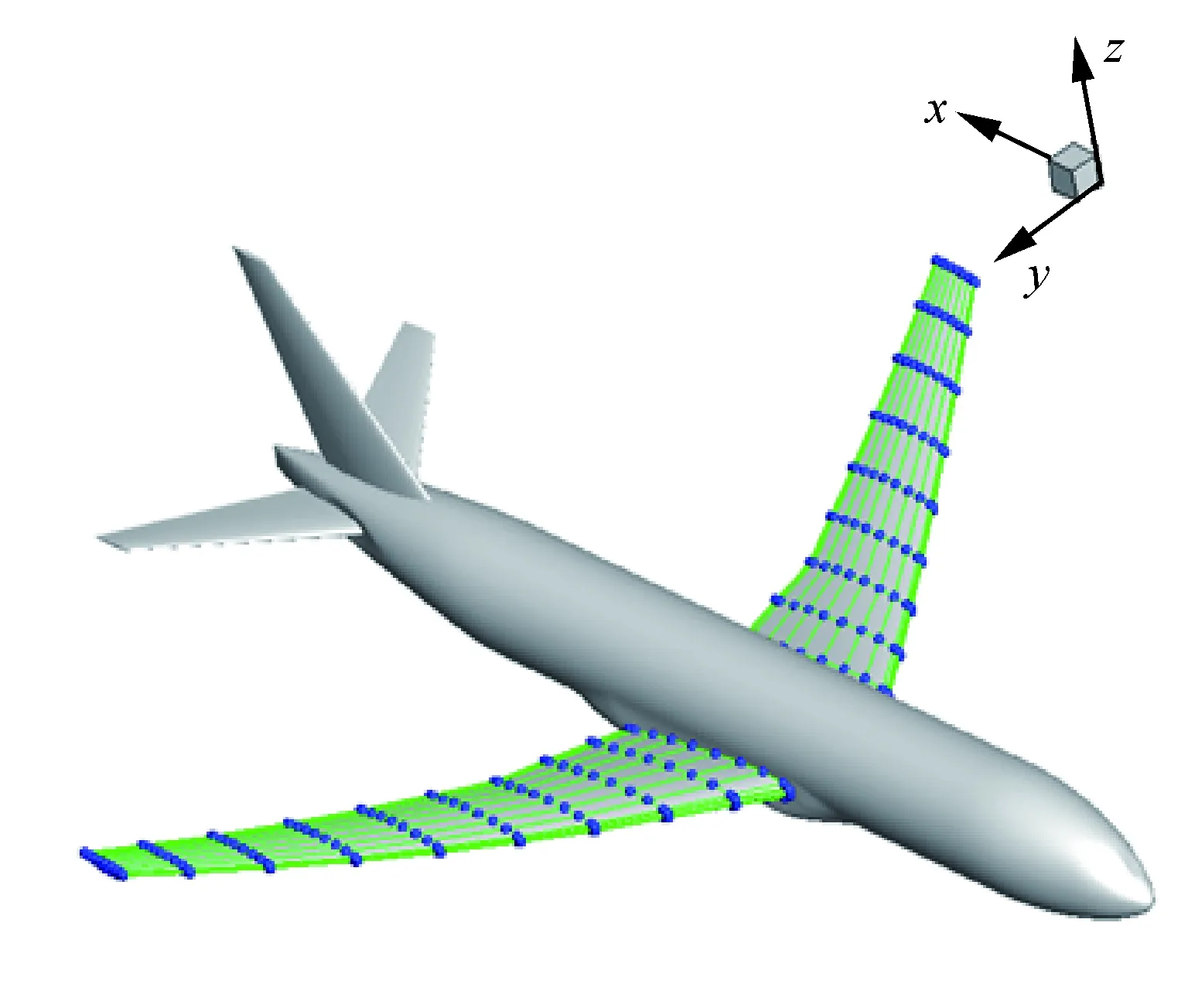
图18 CRM标模参数化Fig.18 Parameterization of CRM standard model

与传统的单点设计一样，基于伴随的优化对多点设计也是通过加权平均来完成，提供给设计人员的选择机会较少，同时又依赖于权重的选取，如果能够充分利用伴随方法的优势，进行有效的多目标设计，对工程来讲是非常有意义的。一种比较有效的途径：首先，可以采用变化权系数的方法，建立设计结果对权系数的数据库，建立以权系数为输入的代理模型，在此基础之上可以进行虚拟非支配解优化，为合理的权系数选择提供非支配解前缘，进一步进行伴随的校核优化。图20给出了本课题组优化软件体系中采用的流程图。

图21给出了基于虚拟非支配解开展多目标优化的结果与单点设计、初始构型典型压力分布形态的对比，其中虚拟Pareto前沿导向的权重偏好目的是马赫数0.87状态相对于巡航状态阻力增加不大于20 counts。从图21可以看出，单点设计结果完全消除初始构型的强激波，多点设计结果压力分布呈现弱激波形态。图22给出了基于虚拟非支配解多目标优化的两设计点阻力验证，该方法在设计点阻力下降近11.7 counts，马赫数0.87状态相对于巡航状态阻力增量为19.1 counts，验证了该方法在工程中的有效性与高效性。

图19 CRM标模的伴随优化Fig.19 Optimization of CRM standard model by adjoint method

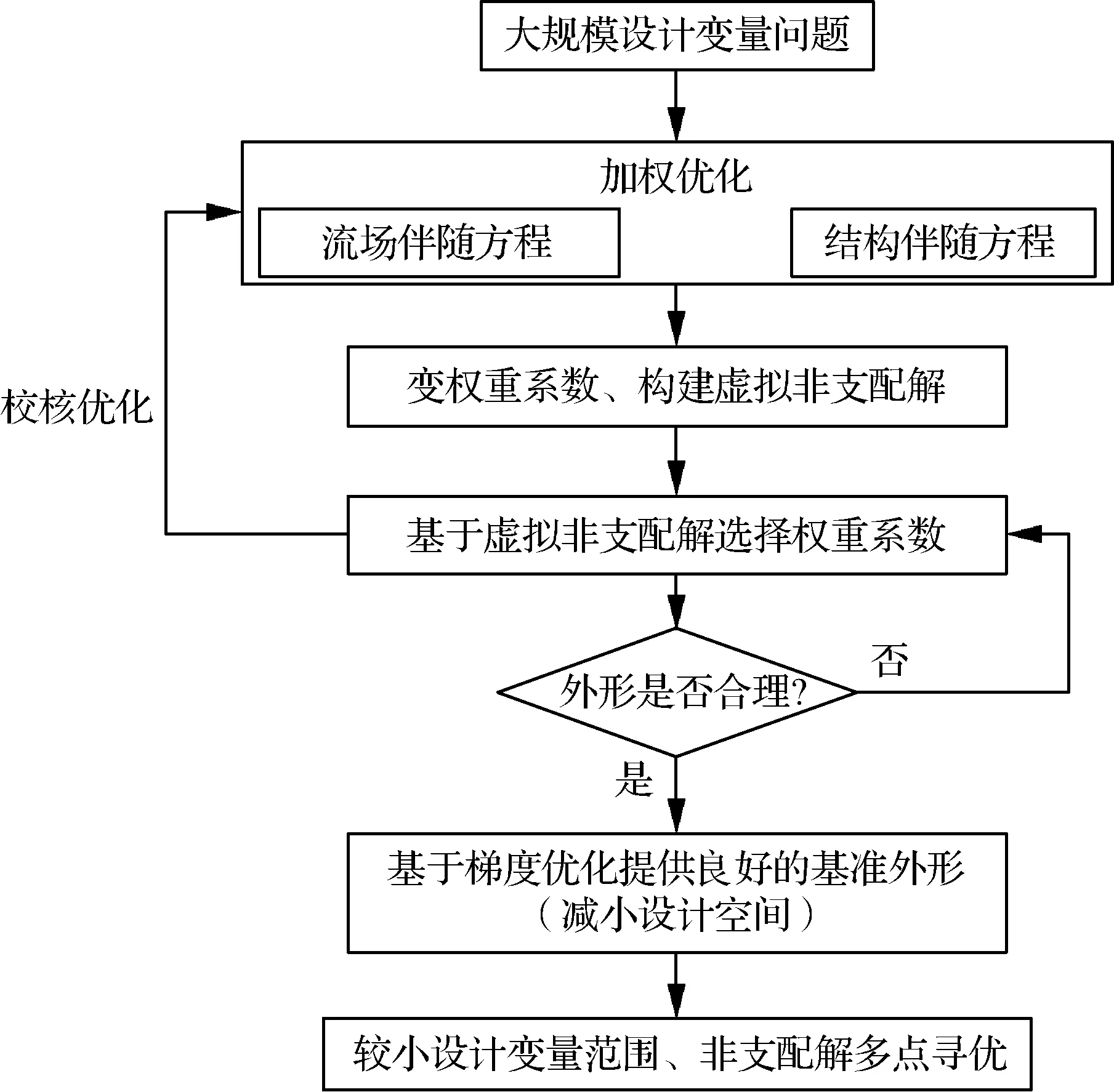
图20 基于离散伴随与虚拟非支配解方法的多目标优化Fig.20 Multi-objective optimization based on discrete adjoint and virtual non-dominated solutions

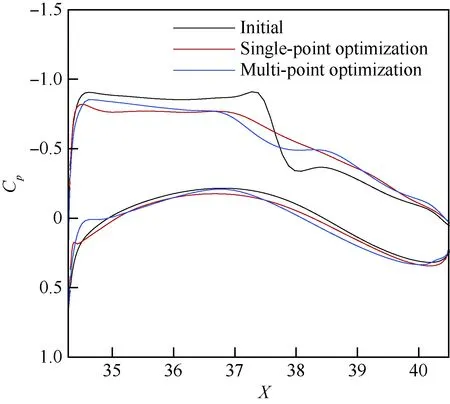
图21 不同Kink位置时设计方法压力分布对比Fig.21 Comparison of pressure distributions of different design methods in kink position

图22 基于伴随方法的多点设计验证Fig.22 Multi-point design verification based on adjoint methods

3.2 基于多学科耦合伴随方程的气动/结构一体化设计

基于智能算法的传统气动结构一体化设计是主导多学科优化的一种手段，此类方法具有程序设计简单、无需太多的学科分析公式推导以及丰富的可行解等优点。但面向大规模设计变量的多学科优化时，尤其是基于高可信度学科分析技术，依然力不从心；即便是较小规模设计变量问题，基于高可信度学科分析技术的优化计算量也是非常庞大的，效率较低。气动结构耦合伴随(Aero-Structural Coupled Adjoint)思想是解决该问题的有效途径，国内在自主研发方面基础比较薄弱。

(7)

(8)

求出延迟伴随变量ψ=[ψaψs]T，可以获取目标函数的梯度：

(9)

气动结构耦合伴随系统是一个涉及气动、结构、流固耦合、网格重构以及对应变分方程的庞大体系，该方法的主要缺点是公式推导复杂，但能够实现梯度计算量与多学科设计变量个数无关，高效率地求出气动力对共用设计变量、气动力对有限元厚度设计变量、冯·米塞斯应力对共用设计变量以及冯·米塞斯应力对有限元厚度设计变量等4种交叉学科导数。

图23给出了AMDEsign耦合伴随优化软件体系中，各个模块之间的变分、调用关系。图24为耦合伴随系统残差随着迭代步数增加而收敛的历程；图25表示阻力系数对设计变量梯度与步长为0.000 1的差分结果之间的对比[98]，其中δ是差分步长。综合与传统方法计算思想、计算效率的对比，可以看出，该项技术是实现气动结构紧耦合设计的一个很有发展前景的方法。

图23 耦合伴随系统Fig.23 Coupled adjoint system

图24 耦合伴随系统残差收敛历程Fig.24 Convergence process of coupled adjoint system

图25 阻力系数对设计变量梯度与差分对比Fig.25 Comparison of gradient of drag coefficient on design variables with differential method

3.3 基于流场/声爆耦合伴随方程的声爆优化

超声速客机、公务机是在民机市场中具有极大发展潜力的一个方向，其中，制约其发展的关键技术是声爆传统的设计手段依然面临计算量大的问题，气动/声爆耦合伴随方程[99]的提出，为高升阻比、低声爆超声速民机设计提供了一个十分可行的技术路径。由于构造声爆伴随方程要求预测值连续可导，因此Burgers方程用来进行声爆预测：

(10)

式中：P为无量纲气压；σ为扩散参数；τ为无量纲时间；Γ为无量纲热黏参数；Cv为无量纲弥散系数；G为射线管面积；c0为声速；ρ0为空气密度。图26为本课题组优化软件的Burgers方程声爆预测模块对地面声爆信号的预测过程示意图，Ma为来流马赫数，α为迎角，Z为距地面高度。

进一步引入伴随算子，构造目标函数：

(11)

式中：lN、D、Q、X、λf、λb、R、p0、T分别为声爆目标函数、设计变量、流场守恒变量、网格坐标、流场伴随变量、声爆伴随变量、流场残差、近场过压以及转换函数，对式(11)中设计变量D进行微分，合并同类项，并令∂p0/∂D、∂X/∂D、∂Q/∂D为0，可以得到气动/声爆耦合伴随方程[99]为

图26 声爆预测过程Fig.26 Prediction process of sonic boom

(12)

进而可以求出地面声爆信号对气动外形的导数为

(13)

在该模块研发中，本课题组优化软件对目标函数的定义采用了2种声爆设计方式，第1种是直接对近场声场分布进行变分，第2种是声爆预测方程耦合变分形式。尽管两种方式目的均为降爆设计，且第1种方式更为简单，但第2种方式直接设计地面声爆信号强度，更为直观，直接可以作为评估结果，在未来高升阻比/低声爆超声速民机中将发挥重要作用。

图27给出了基于流场/声爆耦合伴随系统结合SQP进行声爆优化过程的声爆信号的变化，其中横、纵坐标分别表示时间和地面过压。由图可见，经过9轮优化第2道过压峰值得到有效抑制，表明耦合伴随方法具有极高的优化效率。

图27 优化前后声爆信号对比Fig.27 Comparison of sonic boom signal before and after optimization

3.4 基于伴随方法的机体/推进系统一体化设计

飞行器机体/推进系统一体化设计始终是设计人员关注的发展方向，随着高性能计算与CFD技术的发展，一体化设计开始成为可能。其中考虑进排气影响的飞行器机体-推进系统一体化设计、内外流型面综合设计是一体化设计典型问题代表。对于新概念背负式动力形式的民用飞机气动布局，推进系统的进排气效应对升力面流动形态的影响更为强烈，对设计参数的灵敏度产生重要影响，从而影响精细化设计效果。

与简单外部流动不同，考虑进排气效应的伴随方程必须考虑进排气边界条件的变分，否则将对伴随变量带来较大的误差，从而导致灵敏度信息的误差，对民用飞机尤其是背负式动力形式民用飞机的精细设计带来影响，这也是考虑进排气条件下开展基于伴随方法进行考虑动力影响的一体化设计的核心工作，需要在开展进排气边界条件推导变分的基础上，建立基于伴随方法的机体-推进系统一体化设计技术。图28给出了飞翼布局参数化示意图，其中1～8分别表示控制点所在位置。图29给出了有/无动力条件下设计变量灵敏度对比，图中可以看出动力效应对灵敏度产生一定的影响，设计师如果要充分挖掘一体化设计潜力，必须考虑进排气效应带来的影,图30进一步给出了一体化优化设计前后的压力云图。

图28 飞翼外形FFD参数化Fig.28 FFD parameterization of fly wing

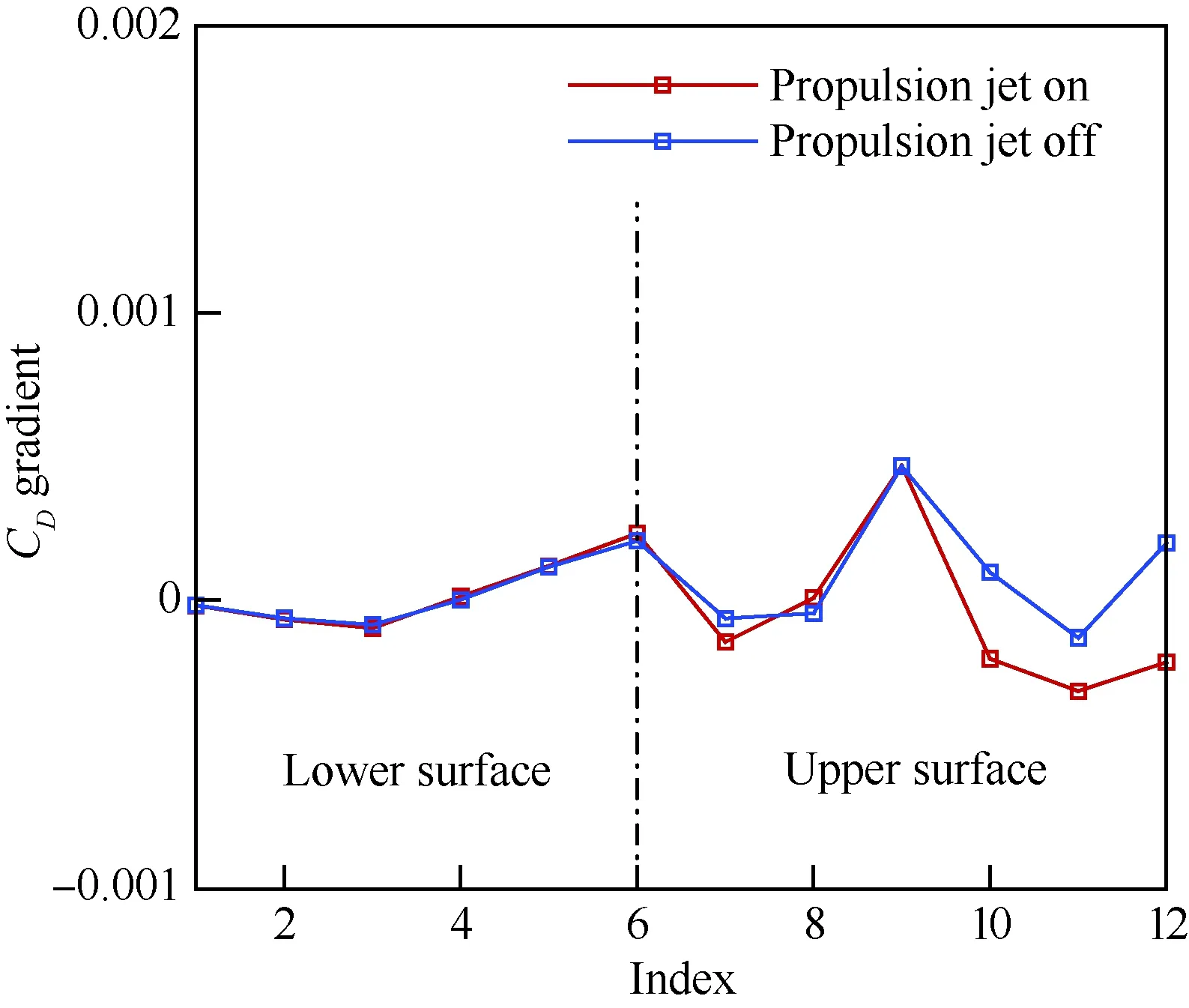
图29 有/无动力条件灵敏度对比Fig.29 Comparison of sensitivity with or without dynamic condition

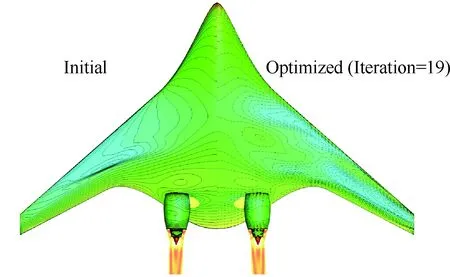
图30 动力条件下一体化设计Fig.30 Integrated design under dynamic condition

4 亟需解决的问题与未来发展方向

目前来看，现阶段气动外形优化方法在民机设计工程应用具有以下亟需解决和关注的问题：

1) 大规模设计变量气动外形多目标优化，高维度设计空间面临的样本规模、计算量庞大等问题，构建高精度代理模型困难等问题。

2) 高维多目标优化中，可视化水平较低，不利于设计人员决策，需要发展有利于设计决策与提高可视化水平的优化方法。

3) 分层协同优化算法的分层策略，以及较高预测精度的代理模型，该技术也是考虑不确定性稳健设计面临的难题。

4) 考虑不确定性稳健设计面临的不确定性分析手段与评价机制。

5) 多学科耦合灵敏度分析手段，无论是基于进化算法还是梯度优化，高效的多学科耦合灵敏度分析方法均能够为优化设计提供最有效的设计空间信息。

6) 高鲁棒性网格生成、重构技术以及可控参数化方法，该部分是实现自动化优化的关键技术，尤其对于总体布局优化相关的大设计空间变形问题尤为重要。

7) 高预测精度代理模型，对于全局优化来讲，提高优化效率最有效的途径就是综合试验设计技术研究、建立高精度代理模型。在满足预测精度的前提下，降低对样本规模的需求，以及样本选取能够最大程度地挖掘设计空间信息。

8) 优化数学模型建模方面。对于优化设计结果影响最大的另外一个要素是优化数学模型的建模，优化数学模型中约束、目标函数的定义直接决定了气动外形优化设计方向。

9) 如何充分高效利用各种优化方法的优势，提高设计效率与设计品质。

10) 目前发展阶段来看，人工设计理念仍然不可替代，应注重设计理念与优化系统的有效耦合。随着高性能计算机技术以及大数据挖掘等关键基础科学问题的研究发展，深度学习未来可以为优化系统提供更为可靠的数据支撑，提高优化体系的建模与决策能力。

工程应用方面，伴随高性能集群、计算科学、优化理论的发展，以及在未来民用飞机市场竞争压力下，民用飞机气动设计技术将向着多学科、一体化、紧耦合形式发展，例如气动结构多学科综合优化，全机考虑动力影响的一体化优化，学科之间高度耦合设计。传统解耦形式下的设计大多是为了解决计算资源不足，降低学科、部件之间的相关性分析难度等问题而做出的让步，随着计算机的进步，以及诸如耦合系统敏度分析、一体化参数化建模等先进理论的成熟完善，一体化、紧耦合优化将在未来工程设计中扮演重要角色，从更深层次充分挖掘气动外形综合设计的潜力。因此，作为飞行器气动外形优化研究人员在工程实践中应更加注重先进设计理论、设计手段的发展，立足型号需求提炼关键基础科学问题，实现方法与应用相互促进、共同发展。

5 结 论

本文系统总结了气动外形数值优化体系中的各个基本要素、关键环节面临的基础科学问题以及实际应用问题，在一些问题的探讨上给出了部分解决思路与建议；提炼了工程应用对设计体系研发的最基本要求；指出了民用飞机气动外形综合设计值得关注的几个关键技术与研究方向；进一步总结数值优化设计亟需解决的基础科学问题与关键技术，展望了数值优化设计未来发展方向。希望可以为数值优化设计研究人员提供有价值的参考，促进国内设计空气动力学与MDO技术的发展。

致 谢：

在本文的研究工作中，刘红阳、余雷、胡星志、郑传宇等同志提供了数据与技术支持，在此表示感谢！