基于分层抽样的不均衡数据集成分类
王馨月,景丽萍
北京交通大学计算机与信息技术学院,北京 100044
不均衡数据分类在实际应用场景中频繁出现,如软件缺陷、自然灾害、信用卡欺诈和罕见疾病监测等[1].以二分类数据集为例,样本数量较少的一类被称为少数类(正类),较多的一类称为多数类(负类),多数类与少数类样本数量的比值称为不均衡度.由于不同类别的样本在数量上存在差异,训练的模型(分类器)在观察数据时,会倾向于对多数类的学习,从而忽略了少数类.传统分类器以优化数据总体的精度为目标,认为对不同类别的误分所导致的误差是相同的,因此为保证训练模型在整体数据集上的预测精度最大化,决策面会向少数类倾斜.当数据集的不均衡度增大时,这种倾斜会更加明显[2].然而在实际应用场景下,少数类往往是更引人关注的一类,提升此类别样本的预测精度往往更为重要.例如,在癌症诊断中,患者远少于未患病的人,这是一个典型的不均衡分类问题.在该应用场景下,将癌症患者误诊为健康人的代价比将健康人误诊为癌症患者的代价要高很多.

图1 随机抽样与分层抽样Fig.1 Random sampling and stratified sampling
为有效处理不均衡数据分类问题,一种简单而有效的方式是对多数类样本进行降采样.然而,当多数类数据呈现出分簇结构时,现有的随机降采样方式容易导致采样样本大多甚至全部来自于其中的一个簇(如图1,空心五角星和圆形分别代表二分类不均衡数据集中的多数类以及少数类样本点;实心五角星表示对多数类降采样得到的样本点),这必然会导致采样样本不能表征原始数据的结构信息.因此,本研究利用分层抽样来挖掘出多数类样本的结构信息,然后按照一定的规则从多数类子簇中抽取一定数量的样本.为减少信息损失并提升分类性能,结合集成学习方法,提出基于分层抽样的不均衡数据集成分类方法(stratified sampling based ensemble classification method for imbalanced data,记为EC-SS),通过分层抽样对多数类进行降采样并保留所有的少数类样本以构造多个均衡数据集,最后构造多个基础分类器来有效地进行不均衡数据分类学习.
下面介绍不均衡分类中的相关工作和自调节谱聚类以及分层抽样的相关知识;提出基于分层抽样的集成学习方法;展示实验结果并进行分析展望.
1 不均衡数据分类方法研究现状
现有针对不均衡数据分类学习的方法可大致划分为外部学习方法和内部方法两大类[3].外部方法主要从改变原始数据集入手,通过采样的方式以期得到相对均衡的数据集合.内部方法则主要通过设计算法来减小传统学习方法对于不均衡数据的敏感性.
1.1 外部学习方法
过采样和降采样是两种常用的采样技术.过采样通常运用随机复制或生成新样本点两种方式增加少数类样本的数量.由于随机复制产生的新点与原有的样本点一样,容易引起模型的过拟合.因此,一系列生成新少数类点的方法被提出.这类方法的两个核心问题在于选择过采样的种子点(用哪些样本点作为参考来生成新点)以及生成器的设计.在选择种子点时,通过正类样本点周边的局部信息,找出正类中相对重要的样本作为过采样的参考点是一种较为常用的方法[4].在设计相应生成器时,线性插值[5-6]和拟合分布[7]是两种常用的方式,前者通过在任意两个样本之间线性插入正类样本点,后者则通过拟合现有少数类点的分布来生成新的样本点.但是当正类样本信息不充分以及不均衡度过高等问题存在时,可能会产生不合适的新样本点[6].
降采样通过减少多数类的样本点均衡两类样本数量.由于随机地移除样本容易损失过多重要性的信息,一系列启发式的降采样策略被提出,如通过数据清除方式来减少多数类中可能存在的冗余或噪音样本点[8].为了最大化利用原有数据避免信息损失,降采样方法通常和集成学习方法相结合以更好地对不均衡数据分类.
1.2 内部学习方法
为减小现有传统分类方法对不均衡数据学习的敏感性,常采用代价敏感学习与集成学习技术.前者通过引入代价敏感策略对不同的类或样本赋予不同的误分代价,并已经和多种传统分类器结合来解决不均衡数据的分类问题,如支持向量机(support vector machine,SVM)[9]、随机森林[10]、神经网络[11]、大间隔分类器[12]和Softmax回归[13]等.后者则主要通过训练众多基础分类器提升最终强分类器的性能,Bagging和Boosting为其中两种最常用的集成学习方法.
在Bagging集成学习方法下,基分类器的数据成员为多次采样得到的子集合,以此构建的弱分类器有相等的权重值.在Boosting集成学习方法下,强分类器由众多权重不等的基分类器组成.在模型训练的过程中,每次被误分的样本会在下一次迭代的过程中提高其误分代价,使之更容易被正确分类.SUN 等[14]利用Bagging技术构造多个基础分类器,并改进传统的分类器融合方式以更好地应用于不均衡数据的分类学习任务.GALAR等[15]提出一种进化版的降采样方法,首先采样多个数据集合,通过比较从中选出最佳子集,并结合boosting进行后续学习.PENG[16]将过采样与集成学习融合,通过对基础分类器的成员数据做不同程度的过采样,然后对每个分类器根据其预测性能赋予不同的融合权重.集成学习方法可以充分利用原始数据,但如何保证数据成员能够保持原有的结构信息,以及弱分类器的差异性和精确性仍是难点问题.
2 预备知识
2.1 自调节谱聚类[21]
利用数据信息(包含n个数据点),可构建数据相似度矩阵A∈Rn×n及其拉普拉斯矩阵L. 自调节谱聚类方法利用局部尺度参数以及能自调节聚类数量策略提升谱聚类性能,从而有效地将n个样本分成K个子集{C1,C2, …,CK}.其中,任意一对样本(如第i个样本si和第j个样本sj)之间的相似度Aij通过高斯核函数计算,同时引入数据点的局部近邻信息调整高斯核参数,具体方法为
(1)
其中,d可为任意距离函数;sg是si第g个近邻;σi=d(si,sg),σj=d(sj,sg). 将聚类数量K作为参数,通过优化如式(2)的损失函数,可实现自调节聚类.
(2)
其中,Z∈Rn×C为X的旋转矩阵,X为由拉普拉斯矩阵L的前K个特征值对应的特征向量形成的矩阵.由此,可得Z=XR以及Mi=maxjZij, 使J最小的K值即确定为将数据划分成子簇的个数.
2.2 分层抽样
分层抽样,又被称作层化抽出法,是一种从总体中抽取样本的方法.首先将整体数据按照某种指定的规则进行分块,来挖掘数据的结构信息.然后,从这些不同的数据块中独立且随机地采样.这种抽取策略得到的样本集合能在一定程度上保持原有数据的总体结构.图1为基于分层抽样的不均衡数据集成分类框架.由图1可见,相比经过分层抽样得到的样本集合,随机抽样的样本集合较难保留原始数据的分布情况,例如可能导致抽样集合的样本大多来自一个簇.
3 基于分层抽样的不均衡数据分类方法
令D={(x1,y1)(x2,y2),… ,(xn,yn)},xi∈Rd(i=1, 2, …,n),yi∈{-1, 1},且D为包含n个样本点的二分类数据集,yi=1表示对应的点属于少数类(少数类数据集记为P),yi=-1表示相应的点属于多数类(多数类数据集记为N), 并且有D=P∪N.
在不均衡数据的分类任务中,往往会引入聚类方法来对数据进行预处理,如将聚类引入到过采样中,使生成数据点的过程在各个子簇内部进行,以避免新产生的少数类点与多数类点样本区域产生重叠[17-19];将聚类技术引入到降采样方法中以期去除噪声点[20],当数据中存在噪声点或异常点时,聚类技术能有效识别远离聚类主区域的小聚类簇,即异常点.
为挖掘大类数据的复杂结构信息,充分利用小类数据,本研究提出一个基于分层抽样的不均衡数据集成分类方法EC-SS.该方法可通过自调节聚类和分层抽样方法构建集成成员数据,并对每个成员训练分类器,最终通过后融合获得分类结果.图2为该方法的学习框架.

图2 基于分层抽样的不均衡数据集成分类框架Fig.2 Framework on Stratified sampling based ensemble classification for imbalanced data
3.1 集成成员数据构建
在二分类的不均衡数据集中,多数类样本数量相对较多,由于直接移除多数类样本会在一定程度上造成信息损失,许多方法则将降采样与集成学习结合,通过多次采样的方式以求充分利用原始数据信息.为进一步保证抽样的样本能够保持原有数据集合的结构信息,本研究利用分层抽样对多数类进行层次化的降采样.
在抽样前,首先利用聚类充分挖掘样本在数据表示层面的内在性质与规律,为进一步的数据分析提供基础.ZELNIK-MANOR等[21]提出的自调节参数谱聚类方法考虑了每个点近邻的局部信息,同时还可以自动选取聚类的数量.为此,本研究利用该聚类算法将多数类样本分为k个不相交的子簇Ci(i=1, 2, …,k), 即N=∪{Ci},i=1, 2, …,k,ni为Ci集合的样本数量.为保证各个集成成员数据的均衡性,从各个子簇中抽取一定数量的样本时,确保最终抽取的多数类样本数量与少数类样本数量一致,即|Nj|=|P|, |P|为少数类样本数;j=1, 2, …,m,j为采样次数索引号.

(3)
(4)
从簇Ci中抽取的样本数ai为
(5)

3.2 集成成员分类器构建与融合
集成学习方法首先利用数据成员训练一组个体学习器,这些学习器可以是相同类型的(同质集成),也可以是不同类型的(异质集成) .如果这些个体均为同种分类器,则这些个体学习器可以被称作基础分类器.
为避免简单的降采样方法导致的信息流失问题,本研究利用分层抽样构造多个均衡的数据集合后,结合同质集成学习方法构造多个相同的分类器,并通过一种常用且简单的后融合技术——多数投票法,来集成所有成员分类器的结果.记每个基分类器为hj,j=1, 2, …,m, 则对应任意一个测试数据x, 其预测结果为hj(x), 最终强分类器H对于x的预测结果为多数基础分类器预测的结果,即
(6)
其中,sign()为符号函数.
将集成学习方法融入到不均衡数据分类问题中具有以下优势:一是通过数据成员的构建不仅充分利用了原始数据集合的信息,同时也避免只使用单分类器容易出现过拟合的问题,此外由于降采样过程的随机性,保证了数据成员之间的多样性,并且本文提出的分层抽样又保证了降采样得到的集合尽可能地保持原有多数类的结构信息.二是通过基础分类器的构建使集成得到的强分类器预测性能优于单分类器的预测性能.此外,集成学习可以很方便地与重采样技术、基本分类器训练算法以及投票方法结合,通过这些组合能更好地提升模型的健壮性与预测性.
4 实 验
为验证基于分层抽样的不均衡数据集成分类方法的有效性,在Musk1、Ecoli3、Glass2和Yeast6这4个不均衡度各异的数据集上,分别探讨集成学习多样性与准确性的关系、采样与融合方式对实验结果的影响、分类器类别及数量对分类性能的影响,并将所提出的分层抽样集成学习方法与处理不均衡分类问题的相关基准算法进行实验对比.
4.1 数据集
实验中使用的数据集的不均衡度从1.29到41.40,不均衡度越大,分类难度越大.数据集具体信息如表1.其中,n为数据集的样本总数;d为样本特征向量的维度;ratio为数据集的不均衡度.
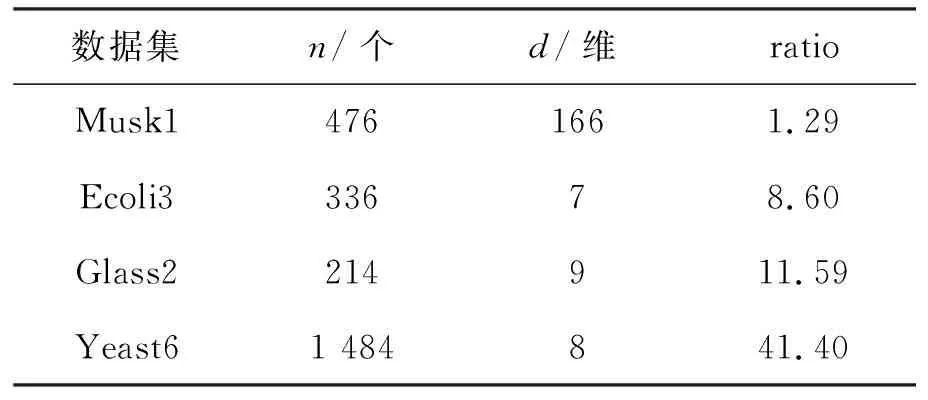
表1 数据集信息表Table 1 Description of four datasets
4.2 对比方法
将本研究提出的EC-SS方法与基于随机抽样的不均衡数据集成分类方法(random sampling based ensemble classification,EC-RS)、自适应采样学习方法(adaptive sampling,AdaS)[16]、基于密度估计的过采样方法(kernel based adaptive synthetic data generation,KernelADASYN)[7]和代价敏感的大间隔分类器方法(cost-sensitive large margin distribution machine,CS-LDM)[12]做对比.其中,EC-SS、EC-RS和AdaS均为集成分类方法,KernelADASYN与CS-LDM分别为处理不均衡数据集的过采样和代价敏感类方法.
EC-RS:对多数类进行随机降采样,然后融合原有的少数类样本来构造均衡的数据集,最后通过构建多个分类器进行分类学习.实验中基础分类器的类型与数量均与EC-SS一致,两者的差别仅仅在于对多数类采取不同的采样方式.
AdaS:将过采样与降采样结合,通过对数据集做不同程度的采样来构造成员数据.其中,基础分类器设为SVM,其数量根据启发式策略自动确定.
KernelADASYN:通过混合高斯模型来拟合少数类样本的分布,其中更靠近边界的点被赋予更高的权重,反之赋予相对低的权重,并利用此分布产生新的少数类样本点.
CS-LDM:基于大间隔分布分类器(large margin distribution machine,LDM)[23],通过对不同的类别引入不同的误分代价惩罚参数,即对少数类样本赋予更高的惩罚参数,使其更容易被正确分类.
在EC-SS方法中固定自调节谱聚类中的近邻参数g=15,其余方法的参数调整与设置均与文献[7,12,16]一致.
4.3 评价指标
本研究采用常用于不均衡数据分类的性能度量指标precision, recall及f-macro来评价各个方法的分类性能.依次定义为
(7)
(8)
(9)
其中,TP为真正例(true positive),即真实类别为正例,预测类别为正例;FP为假正例(false positive),即真实类别为负例,预测类别为正例;FN为假负例(false negative),即真实类别为正例,预测类别为负例.所有实验结果均为5次10折交叉验证(50次实验)的均值与标准方差,最佳实验结果被加粗标记,次之的用下划线标记.
4.4 实验结果与分析
4.4.1 集成学习多样性与准确性的关系
为探讨集成学习中多样性与准确性的关系,本研究用EC-SS以及EC-RS进行如下实验:在固定训练及测试数据情况下,使用SVM分类器在Glass2数据集上进行200次实验,并记录相关实验结果(200个模型的预测结果标签以及f-macro值).统计结果如图3,其中,x轴表示任意两次实验预测f-macro的均值(准确性),y轴表示相应两次预测结果标签的Pearson相关关系 (多样性).从图3可见,EC-SS能在较少地牺牲多样性的情况下获得更高的f-macro指标,即使是在相似的多样性下,EC-SS也比EC-RS更能提升分类性能.
4.4.2 采样与融合方式对实验结果的影响
基于4.4.1节实验的结果,对200次预测f-macro均值的实验结果进行进一步统计,结果如图4.其中,min、avg和max分别表示200次预测f-macro结果的最小值、均值以及最大值.由图4可见,EC-SS比EC-RS更能为集成学习提供有效的数据成员,以提升最终强分类器的预测性能.
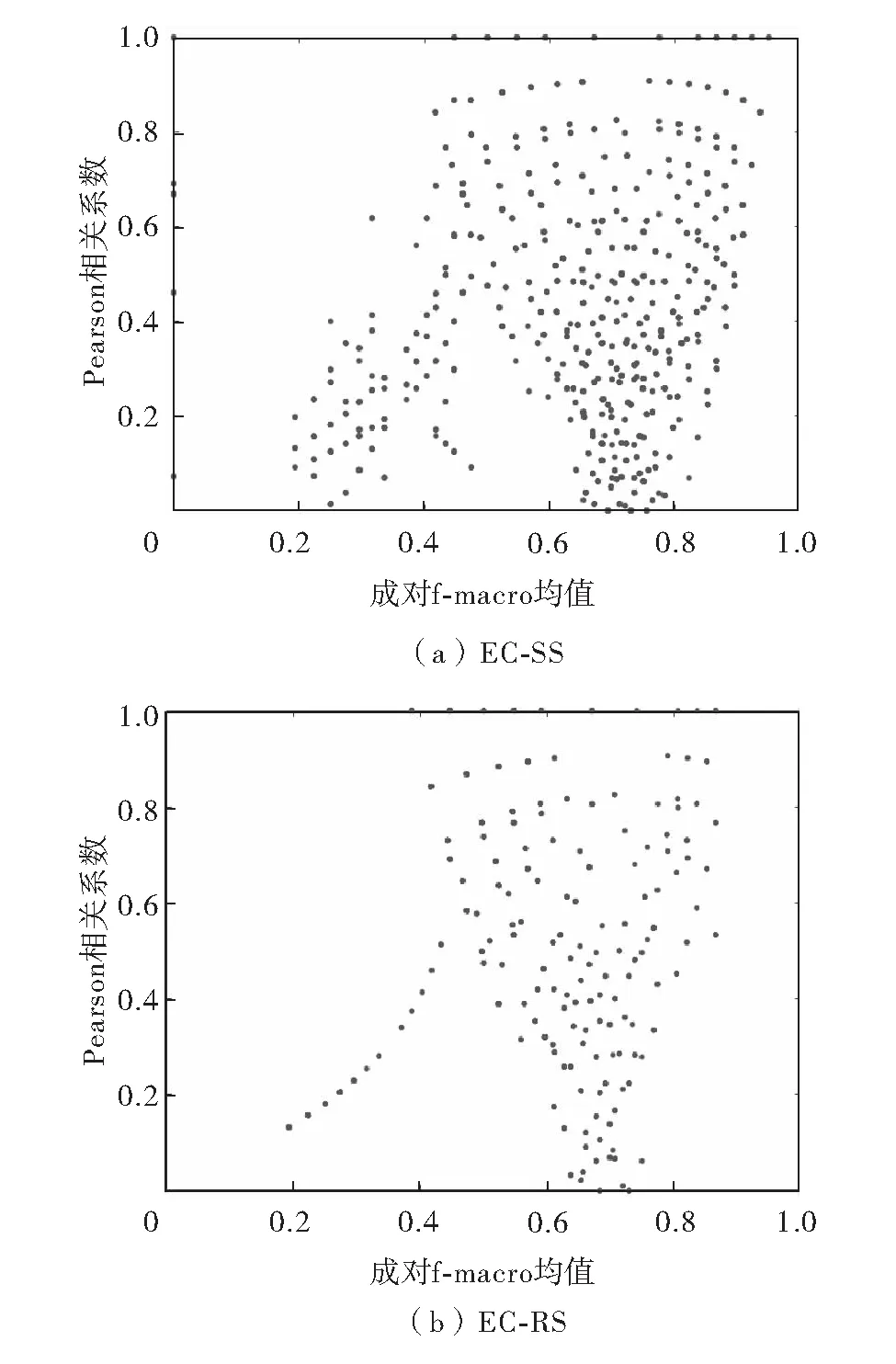
图3 分层抽样与随机抽样在Glass2数据集上经200次实验所得集成成员多样性与准确性的关系Fig.3 Demonstration of the relationships between the diversities and qualities of 200 components for EC-SS and EC-RS on Glass2 dataset

图4 不同采样方式下200次实验结果对比Fig.4 Comparisons of 200 component classification performance based on different sampling strategies
4.4.3 分类器类别及数量对分类性能的影响
为探究分类器类别对分类性能的影响,本研究固定基础分类器的数量为35个,在SVM、最近邻(k-nearest neighbor,kNN, 本研究设k=3)分类器以及决策树(decision tree, DT)3个不同分类器中进行实验.结果如表2,不同分类器中各指标达到的精度各有不同.采用以DT为基础的分类器时,precision和f-macro可达到相对较好的结果,基础分类器为3NN可以达到较高的recall指标.SVM分类器在3个分类器中的分类效果相对较差.综上,后续实验采用DT作为基础分类器.
为探究分类器数量对分类性能的影响,实验中固定基础分类器为DT,并设基础分类器的数量分别为5、15、25、35、45、55和65.EC-SS方法在3个性能度量上随基础分类器数量的变化情况如图5.由图5可见,随着分类器数量的增加,各实验指标在不同数据集上的敏感度有所变化. 如针对Musk1数据集,基础分类器数量超过15个时,3个指标对基础分类器的数量变化相对不再敏感.对于Ecoli3和Yeast6数据集,f-macro值随着分类器数量的增加均具有先降后升再降的趋势,对于Glass2数据集,3个指标对分类器数量的变化均有明显的波动趋势.

表2 EC-SS在分类器SVM、3NN和DT的性能Table 2 Performance of the proposed EC-SS in terms of SVM, 3NN and DT

图5 EC-SS在4个数据集下分类性能随决策树数量的变化Fig.5 Performance of EC-SS on 4 datasets by varying the number of DT
4.4.4 与不均衡分类方法的对比实验
为进一步验证EC-SS的有效性,将EC-SS与基准方法EC-RS、AdaS、KernelADASYN和CS-LDM进行对比.实验中设置EC-SS与EC-RS的基础分类器均为DT,基础分类器数为35个时的实验结果如表3.由表3可见,EC-SS在3个常用的不均衡分类指标上均优于对比方法.此外,通过计算EC-SS相对基准方法在f-macro指标上的提升率(relative improvement, RI)可表示为
RI=(F1-F2)/F2×100%
(10)
其中,F1代表EC-SS方法得到的f-macro值;F2代表其他方法处理相同数据集时得到的f-macro值.以Ecoli3数据集为例,EC-SS方法相对于基准方法(EC-RS、AdaS、KernelADASYN和CS-LDM)的f-macro指标分别提升了0.85%、3.00%、2.62%,和16.75%.由于EC-SS相对不同方法提升率不在同一个数据级别,通过计算log(RI)+2,如图6,EC-SS在很大程度上提升了预测结果.由于EC-SS方法中的聚类学习充分挖掘了多数类中的结构信息,并且分层抽样有效地保留了多数类的原始分布情况,最终结合集成学习方法使之对不均衡数据分类有所提升.
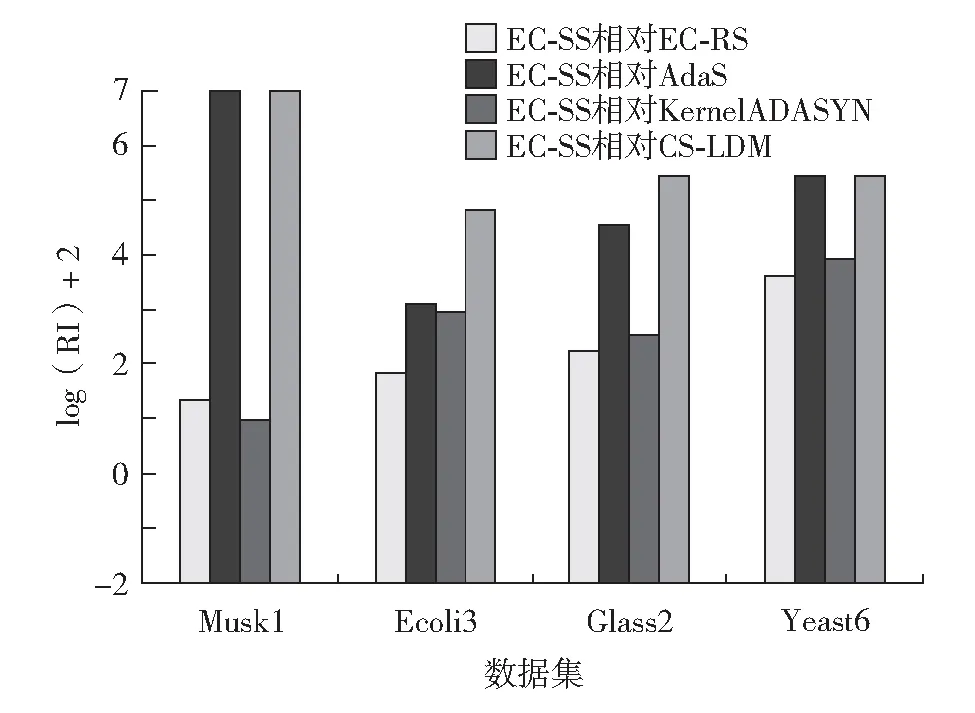
图6 F-macro指标相对提升率Fig.6 Relative improvement in terms of f-macro
为显著性分析预测结果,以95%的置信度将对比方法的实验结果(表3)进行方差分析(analysis of variance, ANOVA)[24],所得p-value值如表4.如果p-value的值低于1×10-5,则表明实验结果具有一定的显著性,由表3数据可以发现,所提出的EC-SS方法相对其余算法的提升具有显著性.

表3 不同算法的precision、recall和f-macro值Table 3 Precision, recall and f-macro of the comparative

表4 方差分析的p-value值Table 4 Statistical ANOVA test results (p-value)
4.4.5 时间性能
表5记录了各个对比方法在固定参数下运行一次需要的平均时间,即50次实验运行时间的均值(包括串行构建分类器所用的时间).用于计算时间的电脑的处理器为第6代英特尔酷睿i7处理器.由于EC-SS、EC-RS以及AdaS均为集成类学习法其时间性能受到分类器的构建的影响,又因为EC-SS方法结合了聚类学习,其时间性能也会受到聚类方法的影响.对比EC-SS和EC-RS的耗时可以看出,在相对小的数据集上两者的运行时间相差不大,在较大的数据集上由于自调节谱聚类的时间复杂度较高,使两者在Yeast6数据集上运行时间相差较大.本研究旨在探讨如何更合理地构建集成学习中的数据成员,以上实验结果表明,基于聚类的分层抽样方法能够构建保持原有数据结构信息的抽样数据集,进而提升最终分类器的预测性能.实际在挖掘多数类结构信息时可以运用更快速的聚类方法以提升运行速度.此外,由于各集成的数据成员以及分类器之间不存在依赖关系,本研究提出的集成分类方法可以实现并行操作,节省运行时间.
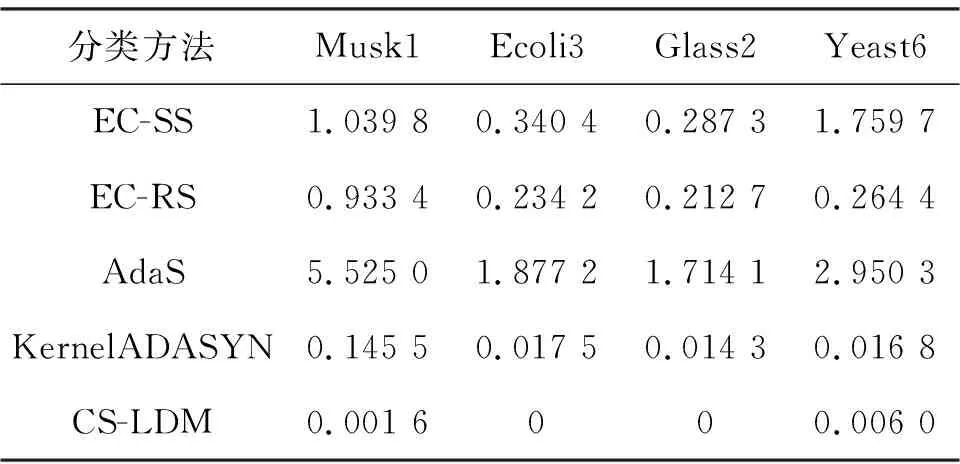
表5 不同算法时间性能Table 5 Running time of comparative methods s
结 语
作为分类问题中的重要研究方向,不均衡数据分类在数据挖掘以及机器学习领域获得了广泛的关注,由于现有不均衡分类方法对于样本的随机采样可能会导致重要信息的丢失,因此本研究提出了基于分层抽样的集成分类算法.首先通过自调节的谱聚类充分挖掘多数类的结构信息,然后通过分层抽样从各个聚类簇中抽取合理数量的样本以构造均衡数据集合,数量的确定则由簇内样本分布的离散程度决定,相对离散的簇中抽取更多样本作为当前簇的代表,相对密集的簇中则抽取相对少的样本,以此来保持抽样集合保持原有数据集的分布特性.最后基于这些均衡的数据成员构造集成分类器.本研究通过一系列实验探究了所提方法对基础分类器类型与数量的敏感度,并通过实验验证了基于分层抽样的不均衡数据集成分类方法可以有效提高分类性能.后续工作拟将分层抽样策略用于多分类问题.

