基于几何滤波效应的高速列车牵引变压器悬挂参数设计

贺小龙，张立民，鲁连涛，罗天洪

(1.重庆文理学院 机电工程学院，重庆 402160; 2.西南交通大学 牵引动力国家重点实验室, 成都 610031)

牵引变压器是高速列车车下的关键设备。因其自身质量大，自带复杂激励源，极易与高速列车车体产生耦合振动等特点，其悬挂参数的设计一直是国内外学者研究的重点。比如Luo等[1]基于车辆的有限元模型研究了车下设备的悬挂位置、频率和设备的质量对车体模态的影响，通过传递函数研究了设备的悬挂参数和车体模态频率的匹配关系;Sun等[2]建立了刚柔耦合的车辆-设备耦合系统模型，并基于协方差的方法分析了车下设备对车辆乘坐舒适性的影响，并研究了设备悬挂参数和车辆的运行速度对乘坐舒适性的提高的积极作用;Dumitriu[3]在考虑单个设备与车体耦合的情况下研究了车辆系统振动特性；Sun等[4]从理论上研究了车下设备对车体振动传递特性的影响，定义了车体的名义垂向一阶弯曲模态频率，并结合数值计算、振动传递分析与模态试验，分析了车下设备悬挂参数对车体模态频率的影响机理，并提出将车下设备设计为动力吸振器可以有效抑制车体在垂向弯曲频率处的振动思路；同时研究了车下设备的悬挂静扰度对车辆运行平稳性及设备本身的影响，并基于隔振理论对设备悬挂的静扰度值进行了确定[5-6]。为了降低车体的弹性振动，石怀龙等[7-8]将车体考虑成弹性欧拉梁，基于动力吸振原理对多个车下设备的最优悬挂频率进行了设计，同时研究了不同设备悬挂频率、联接阻尼、质量和安装位置条件下的车体振动分布规律；吴会超等[9]建立了车辆设备的刚柔耦合模型，研究了设备刚性吊挂与弹性吊挂对车体振动的影响，确立了车下设备弹性悬挂参数与车体结构之间的匹配关系。

从以上研究成果可以看出，目前国内外学者对车下设备的悬挂参数设计有了一定的研究，且形成了初步的设计理论，但是还远远不能满足我国高速动车组的设计的需求。目前对于车下设备悬挂参数设计主要依据既有工程经验和消极隔振理论进行，并未考虑车辆系统具体结构、运营环境、结构参数等因素的影响，未形成成熟的设计理论体系、设计规范和行业标准。对此，本文在研究了车辆设备耦合振动机理的基础上，分析了车辆系统滤波效应对车辆振动的影响，并考虑将变压器悬挂频率设计为与车辆滤波频率重合来设计变压器悬挂频率，最后利用数值积分法验证车体弹性振动的衰减效果。本文的研究结论可以为车下大质量设备的悬挂参数设计提供思路。

1 车辆设备系统建模

考虑车体的弹性振动对于研究车辆系统振动特性显得尤为必要[10]。文中对所建立的车辆设备系统模型模态进行了一定缩减，以减少计算量，模型中考虑了车体带有阻尼元件和弹性元件的二系悬挂系统。同时车辆的构架及其附属部件均被忽略，并且将二系悬挂位置考虑成轨道不平顺输入的两个点。令前、后转向架的垂向位移输入分别为Zf、Zr，车辆模型示意图如图1所示。

(a)车辆设备耦合系统

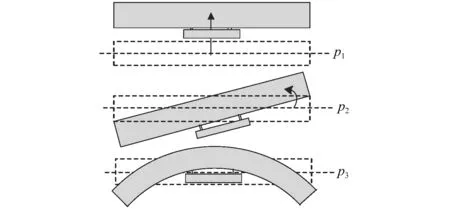
(b)车体三阶模态图1 车辆设备耦合系统以及模态Fig.1 Vehicle equipment coupling system

其中以车体的沉浮(p1)、点头(p2)、弯曲(p3)来描述车体的运动，以设备的沉浮(p4)、点头(p5)来描述设备的运动。模态坐标可以描述为[11]

pT=[p1p2p3p4p5]

(1)

车辆系统的运动可以描述为以下运动微分方程

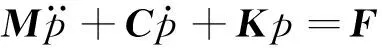
(2)

车辆系统质量矩阵表述为

式中：Mc,Jc,Mb,Me,Je分别为车体的质量、点头转动惯量、车体弯曲的模态质量、设备的质量以及设备转动惯量。定义kzc为单个构架二系悬挂刚度，kb为车辆的抗弯刚度，czc为单个构架二系悬挂阻尼，cb为车辆的结构阻尼，kzc,czc分别为设备悬挂刚度和悬挂阻尼。车辆系统的刚度矩阵、阻尼矩阵分别为

d为车辆定距，Zb1,Zb2分别为车体二系支撑处车体的垂向位移，Zb3为变压器悬挂处车体的垂向位移。因轨道不平顺引起的车体垂向位移分别为zf,zr，此时二系悬挂与车体作用力分别为

(3)

车体上任意一点的垂向振动响应Zk可以由车体的三阶模态叠加而成，且有

Zk=p1+bkp2+Zbkp3

(4)

式中:bk和Zbk分别为二系悬挂位置与车体中部的纵向距离和车体沿纵向任意点垂弯模态位移。式(4)可以表述为

Zk=Λkp

(5)

式中:Λk为模态坐标p与车体垂向位移相关联矩阵，且有

Λk=[1bkZbk]

(6)

为了快速得到车体在受到轨道不平顺激励时车体的垂向振动响应，采用如下坐标形式

p=Uq

(7)

式中:U为无阻尼系统的模态矩阵;q为模态阵型向量，式(7)可以转换为

qT=[q1q2q3q4q5]

(8)

式(1)中的向量p为无支撑车体模态向量，式(8)中q为车体弹性支撑时车体模态向量。将式(7)代入式(2)中，并通过左乘UT，可以将式(2)中的广义坐标p进行解耦

(9)

经过转换，车辆系统运动方程可以表达为

(10)

式中:fi=U(i)TF,U(i)T为第i阶模态向量的转置表达式。车体的第三阶模态为车体的垂向弯曲模态，因为其低刚度特性，二系悬挂对车辆的垂向弯曲固有频率和固有阵型影响微乎甚微。有研究结果表明，考不考虑车体二系支撑对研究车体的垂向弯曲模态的振动影响可以忽略。通过求解式(9)，车体任意点的响应可以表述为

(11)

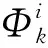
(12)

因为车辆系统受到的轨道不平顺激励是一个随机过程[12]，通常采用功率谱密度函数描述轨道不平顺。车体任意一点k垂向响应Zk的功率谱密度Szk(ω)根据多自由度系统受随机激励计算理论得出

(13)

其中，

为广义力fm(t)和fn(t)激励谱矩阵，m，n=1，2，3；

为频率响应函数的对角矩阵。此时式(13)可以表述为

(14)

式(14)解释了广义力fm(t)和fn(t)广义力激励频谱Sfmfn(ω)如何联合作用于车体使车体产生响应。其中广义力互谱Sfmfn(ω)与轮轨前后激励互谱存在如下关系

(15)

对于车体的第三阶垂向弯曲模态，Sf3f3(ω)可以描述为

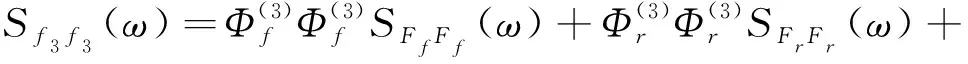
(16)

因为前后轮轨激励存在时间滞后关系，由此可得前后轮轨激励力的频谱存在如下关系[13]

(17)

将式(16)代入式(15)可得

(18)

其中二系前端构架车体连接点所受激励力表述为

SFfFf(ω)=[k2+ω2c2]SW(ω)

(19)

将式(19)代入式(18)可得给定速度下激励力的互功率谱函数。

2 滤波效应分析

对于轨道的几何滤波效应的研究，文献[14]对其进行了定义：在与悬挂系统共同作用下，会产生车辆或者车辆某阶模态阵型对轨道某些不平顺波长激励没有响应的现象，这一现象称为几何滤波效应。这种现象在本文所研究的车辆设备耦合系统中，就显示为轨道激励谱密度出现连续的谷值。其中车辆的运行速度仅影响激励谱的幅值，但是不会改变谱的形状，随着车辆运行速度的增加，激扰峰值频率也逐渐改变，如图2所示。

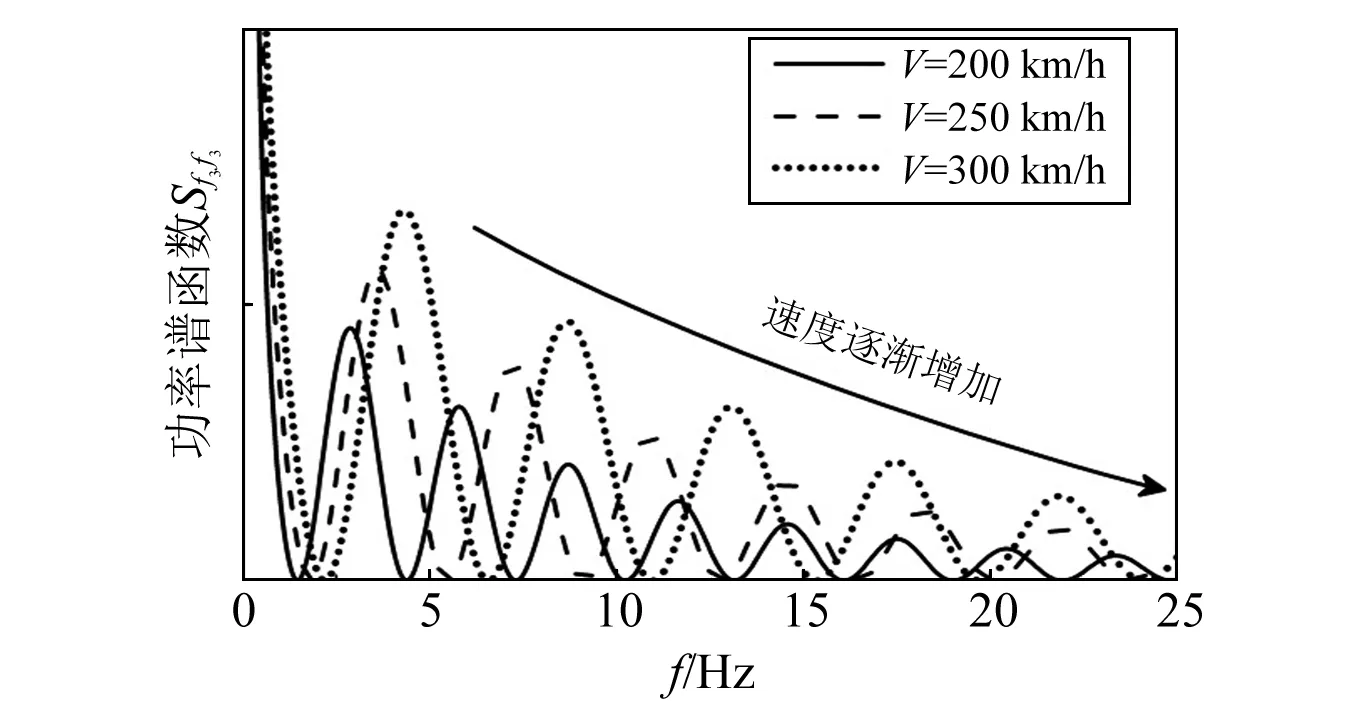
图2 激励谱随速度变化趋势图Fig.2 The trend chart of excitation spectrum with velocity change

由式(18)可知，要使Sf3f3为零，那么可得

1+cos(ωτ0)=0

(20)

由式(20)可求得车体垂向弯曲振动响应取最小值的频率条件为

(21)

式中:V为车辆运行速度，km/h；d为车辆定距，m；n=0，1，2，。依据式(21)可求得滤波频率随速度变化趋势如图3所示。

图3 滤波频率随速度变化趋势图Fig.3 The trend chart of filter frequency variation with velocity

由图4计算结果可知轨道激励谱和车辆的频响函数是影响车辆振动响应的两个因素，对于给定的轨道不平顺，车辆的速度直接关乎轨道不平顺激励函数；而牵引变压器悬挂参数往往直接影响到车辆的频响函数。一般高速列车具有特定的设计运营速度，因此牵引变压器悬挂参数成为了对车辆振动特性影响的主要因素。

(a) (b)图4 不同速度下车体垂向弯曲模态激发时响应Fig.4 The response of for different speed

图5计算了变压器弹性悬挂时车辆速度250 km/h条件下滤波效应对车体弹性振动的影响。图中滤波频率出现在2.0 Hz,5.9 Hz,9.8 Hz,13.7 Hz和17.6 Hz附近。其中牵引变压器悬挂频率比变化范围选取为0.5～2.0。由图可知，车体的两阶垂弯模态频率随着变压器悬挂频率比增加逐渐增加，车体的低阶垂弯频率不会超过车体未悬挂变压器垂弯频率。同时对于车体的垂弯振动响应谱，车体在5.9～9.8 Hz内振动出现了峰值，仔细研究发现在该频段内不存在滤波频率，并且激励能量在该频段内较大，因此分析车体在该频段出现的峰值为车体受到较大激励能量导致的强迫振动。尤其注意到其中当变压器悬挂频率比取值0.7时车体低阶垂弯模态频率正好处于激励峰值，导致车体垂弯产生大幅振动。同时车体振动在9.8～13.7 Hz内出现较大峰值，而车体的低阶垂弯模态频率正好处于该频段范围内，且滤波效应在该频段内不存在滤波频率点，分析可知该现象为车体低阶垂弯模态在轮轨激励作用下引起车体振动。当变压器悬挂频率比为0.5时，车体高阶垂弯模态频率正好处于滤波频率处，因此车体在高阶垂弯频率处振幅为零。在其余悬挂频率比条件下，虽然车体高阶垂弯模态频率与滤波频率不重合，但是由于此时轮轨激励能量较小，车体的高阶垂弯模态振幅基本可以忽略不计。

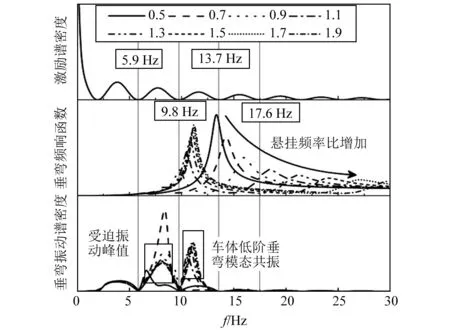
图5 不同变压器悬挂频率比对车体振动响应(V=250 km/h)Fig.5 The response of vehicle vibration (V=250 km/h)

图6计算了变压器弹性悬挂车辆速度350 km/h时滤波效应对车体弹性振动的影响。图中滤波频率出现在2.7 Hz,8.2 Hz,13.7 Hz和19.1 Hz附近。其中牵引变压器悬挂频率比选取为0.5～2.0，与图5中所述结果类似，车体的两阶垂弯模态频率随着变压器悬挂频率比增加逐渐增加，其中车体低阶垂弯频率不会超过车体未悬挂变压器垂弯频率。在车体的垂弯振动响应谱中，车体振动在2.7～8.2 Hz出现了峰值，但振幅较小，分析发现此时虽然激励能量较大但是车体低阶垂弯模态频率不处于该频段范围，导致车体在该频段振幅较小。同时车体振动在8.2～13.7 Hz出现较大振动幅值，此频率范围正是车体低阶垂弯模态频率所处频段，且轮轨激励在该频段具有较大能量，所以车体在该频段具有较大振幅。在13.7 Hz以上频率，车体振幅较小，之所以会产生这种现象要么因为车体高阶垂弯频率正好与滤波频率重合，要么因为轮轨激励能量较小。

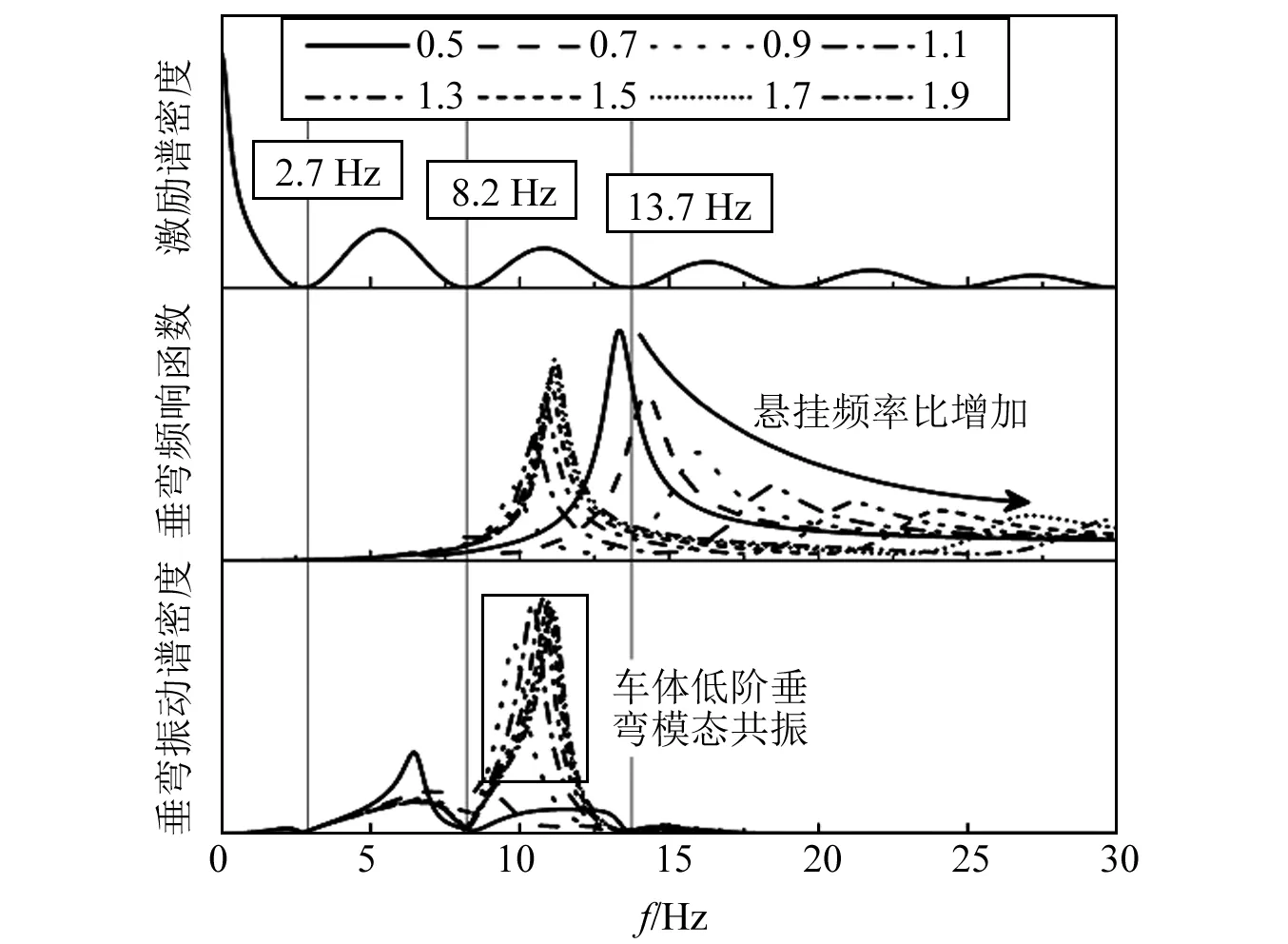
图6 不同变压器悬挂频率比对车体振动响应(V=350 km/h)Fig.6 The response of vehicle vibration (V=350 km/h)

综合图5、图6可知：在低频范围车体极易因为激励能量过大引起车体产生强迫振动；两种运行速度下，车体的低阶垂弯模态与激励共同作用导致车体产生较大振动幅值；车体的高阶垂弯模态因为滤波效应或者因为激励能量过低导致车体在高阶垂弯模态频率时振幅较小。

根据以上分析，可以做出以下思考：

(1)既然车体的弹性振动一直是车辆振动控制的重要对象，车辆系统的滤波效应又可以对车体的垂向弯曲振动起到衰减作用，那么可以考虑基于该效应来控制车体弹性振动；

(2)当车辆悬挂诸如牵引变压器等大质量设备后，车体的垂向弯曲模态将发生改变。车体的两阶弹性模态将对车体振动产生影响，因此可以考虑将悬挂变压器后的车体两阶垂弯模态频率设计为滤波频率或者尽量靠近滤波频率，使得车辆的弹性振动得到衰减。

3 基于滤波效应的变压器悬挂频率设计

综合以上分析可知，车辆系统对于车体的弹性振动具有滤波效应，尤其对车体的低阶垂弯模态影响明显。在变压器悬挂参数设计中可以利用这一特性，考虑将车体低阶垂弯模态频率设计为相应速度下滤波频率，以此来抑制车体弹性振动，其设计思路如图7所示。

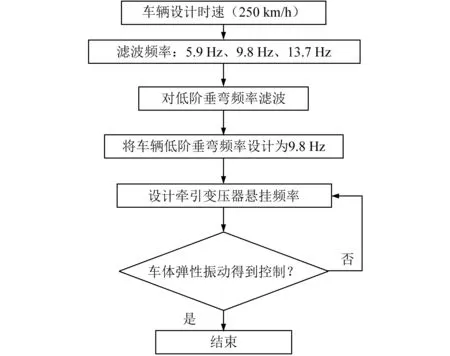
图7 变压器悬挂频率设计思路Fig.7 Design idea of transformer suspension frequency

以车辆设计时速250 km/h为例，设计牵引变压器悬挂频率时考虑将车体的低阶垂弯模态频率设定为9.8 Hz为宜。根据之前的变压器悬挂频率与车体两阶垂弯模态频率变化关系，可以选择出变压器的悬挂频率如图8所示。

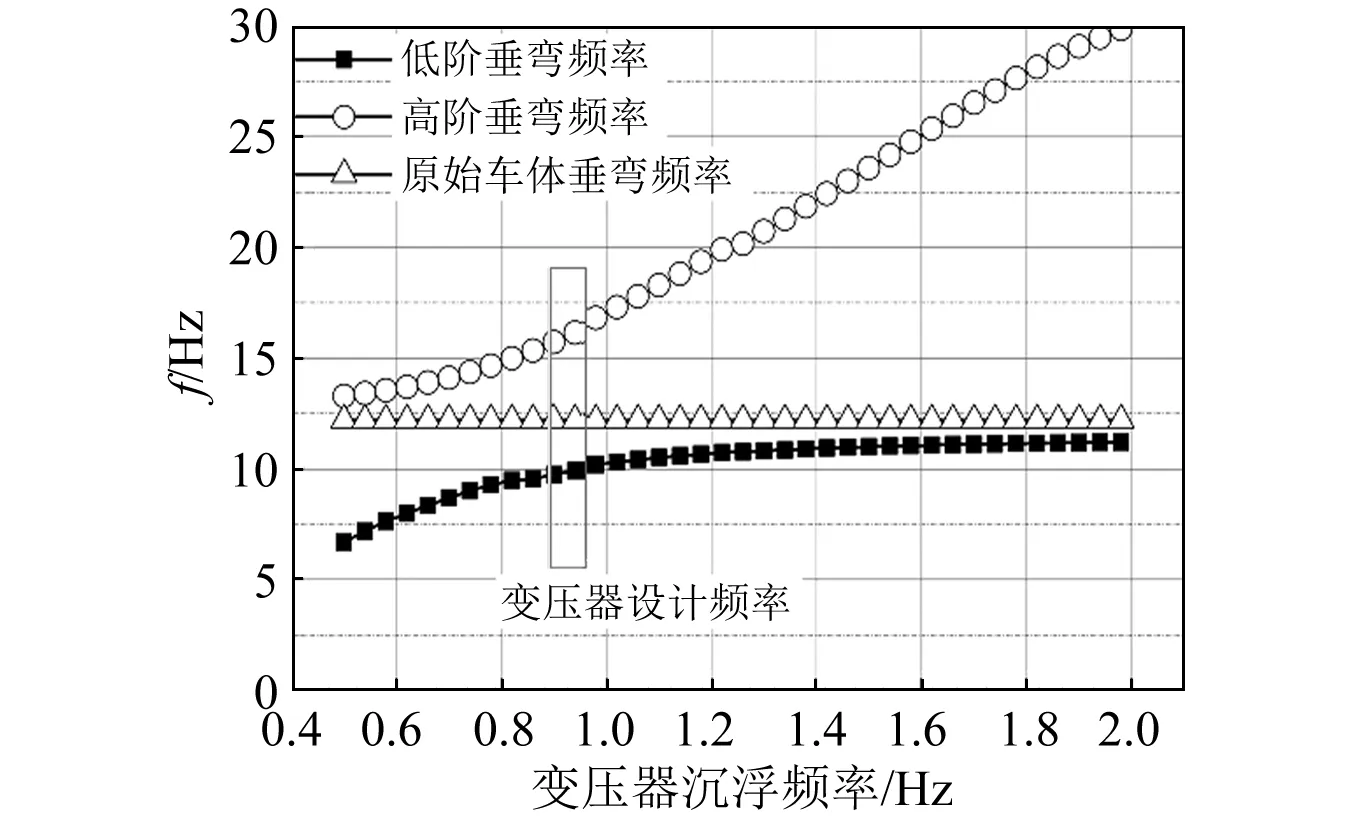
图8 变压器沉浮设计频率Fig.8 Bounce frequency of traction transformer

图9 变压器悬挂频率比取0.92垂弯振动响应Fig.9 Vertical bending response when ratio chose as 0.92

由图8可知，变压器悬挂频率比选择为0.92时，车辆的低阶垂弯频率正好能与9.8 Hz滤波频率重合，车体垂弯振动响应如图9所示。由图9可知，当牵引变压器悬挂频率比取值为0.92时，车体垂向弯曲在10 Hz以内受到的强迫振动幅值除了比变压器悬挂频率比取值0.5低以外，比其余条件下振幅略高但是这种差异不大；对于垂弯模态在10 Hz以上频段振动幅值，变压器悬挂频率比取值0.92具有明显优势。

为了弄清楚变压器取值0.92时车体弹性模态振动的改善，图10计算了时速250 km/h条件下，车体弹性模态振动特性。图中比对了基于滤波效应设计变压器悬挂频率条件下车体弹性振动及变压器振动烈度。由图可知，当牵引变压器悬挂频率比设置为0.92时，车体中部振动无论是舒适度指标还是振动加速度有效值，均有一定的提升。其中变压器悬挂频率比取值0.7时车体中部弹性振动最小，但是此时牵引变压器自身振动烈度也最大，并且超过4.5 mm/s。综上分析可知，将车体低阶垂弯模态频率设计为与车辆特定运行速度下的滤波频率重合能显著降低车辆的弹性振动。

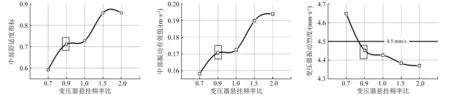
(a)车体中部振动舒适度指标 (b)车体中部振动有效值 (c)变压器振动烈度图10 车体弹性模态振动特性Fig.10 Elastic vibration characteristics of car body

4 结 论

为了对高速列车牵引变压器悬挂参数进行设计，本文提出了一种基于几何滤波效应的变压器悬挂参数设计思路。其研究结论如下：

(1)在低频激励时车体极易因为激励能量过大引起车体产生强迫振动；两种运行速度下，车体的较大振动主要由车体的低阶垂弯模态与轮轨激励共同作用引起。

(2)车体的高阶垂弯模态要么因为滤波效应或者因为激励能量过低导致车体在高阶垂弯模态频率处振幅较小。

(3)对于设计时速250 km/h高速列车为例，基于滤波效应将变压器悬挂频率设置为9.8 Hz，可以显著衰减车体的弹性振动。