基于超球优化支持向量数据描述的滚动轴承故障检测

林 桐，陈 果, 滕春禹，王 云，欧阳文理

(1. 南京航空航天大学 民航学院，南京 210016； 2. 中航工业综合技术研究所，北京 100028)

由于单一特征易受外界条件干扰，不同特征对不同故障的灵敏度不同等原因，在滚动轴承的振动监测中仅依据某一特征量评估轴承状态，其效果往往不够理想。为保证评估方法对各类故障均较敏感且有较好的鲁棒性，滚动轴承的状态评估应该充分利用时域、频域和时频域等多维特征信息，进行特征融合[1]。

BP神经网络[2-3]、支持向量机[4-5]、稀疏分类[6]等特征融合方法已广泛应用于滚动轴承故障诊断。但是，这些方法均需要多类故障数据作为支撑，而实际工程中，滚动轴承的故障样本通常难以获取。为了在仅有正常运行数据的情况下实现滚动轴承的故障检测与退化评估，高斯混合模型[7-8](Gaussian Mixture Model，GMM)、自组织特征映射[9-10](Self-Organizing Map, SOM)和支持向量数据描述等方法被相继应用。Chen等在提取了时域和频域特征的基础上，采用高斯混合模型对训练数据进行描述，并通过主分量分析(Principal Component Analysis, PCA)对多维特征进行降维；Yu认为相比于PCA，通过保局投影(Locality Preserving Projections, LPP)能得到更有意义的低维特征，并采用基于GMM的负对数似然估计作为轴承性能劣化的评价指标；李巍华等对轴承各运行状态建立相应的GMM模型，通过计算对应状态GMM相对基准模型的偏离程度判断轴承退化程度。Huang等将自组织映射和BP神经网络的结合，对轴承进行性能评估和寿命预测；张全德等采用自组织特征映射，通过计算样本到神经元权向量的最小匹配距离来评价滚动轴承的状态；Tax等[11]认为GMM等方法的缺点在于需要大量训练样本，在特征维数较高的情况下问题更加突出，并提出了支持向量数据描述方法，能在小样本情况下较好地解决一类分类问题。潘玉娜等[12]提取小波包分解节点能量作为特征量，通过SVDD(Support Vector Data Descirption)融合后对轴承退化程度进行了评估；Shen等[13]为得到更加鲁棒的滚动轴承劣化评价指标，将模糊逻辑和SVDD结合，提出了基于模糊SVDD滚动轴承状态评估方法；此外，郝腾飞等[14]将SVDD推广至半监督情况，提出了一种基于小球大间隔的滚动轴承故障检测方法；文献[15-16]将多核学习引入SVDD，通过仿真数据对多核SVDD进行了研究。

SVDD的本质是将输入特征映射至高维特征空间后，通过在特征空间寻找最小体积超球实现数据域的描述。显然，SVDD有效的前提是特征空间中特征向量的分布能较好的通过超球来描述，因此，核函数的选择尤为关键，当核函数与输入特征相匹配时才能获得更优的性能。然而，特征向量在高维空间上的分布十分复杂，在没有先验知识的情况下选择或构造合适的核函数十分困难，这将导致特征空间中SVDD预测的描述边界未必能与真实边界很好地贴合。如图1所示，当预测的描述边界与正常样本的实际边界有所偏差时将会带来两类误差：①将正常样本误判为异常；②将异常样本误判为正常；这将直接影响滚动轴承故障检测的准确率。

既然特征空间分布的复杂性会为边界的描述带来困难，那么改善特征的空间分布就有望降低数据描述任务的难度，进而提高滚动轴承故障检测的准确率。为此，本文提出了一种超球优化支持向量数据描述的滚动轴承故障检测方法。

图1 预测边界与实际边界偏差所引起的两类误差Fig.1 Two kinds of errors caused by the deviation of prediction boundary and actual boundary

1 超球优化支持向量数据描述方法

1.1 特征提取

1.1.1 时域特征提取

表1 带量纲时域特征Tab.1 Dimensional time domain features

无量纲特征包括：波形因数Sf、峰值指标Cf、冲击指数Lf、歪度Sv、峭度Kv和裕度指标If，定义如表2所示。

表2 无量纲时域特征Tab.2 Non-dimensional time domain features

1.1.2 频域特征提取

不同阶段的轴承损伤将影响其频谱，因此可以从信号频谱中提取出相应频域特征，本文提取的频域特征包括：重心频率FFC、均方频率FMSF和频率方差FVF，定义如表3所示。其中，Sf为信号频谱函数。

若把频谱看成横放于坐标轴上的一根杆的质量密度函数，那么重心频率是这根杆的重心坐标，低频幅值较大可以看成杆原点附近的密度较大，重心将在原点附近，重心频率的值较小，反之，当重心距离原点较远，重心频率将较大；均方频率是杆绕原点的惯性半径的平方，当原点附近的密度较大时，惯性半径较小，均方频率的值较小，反之，则惯性半径较大，均方频率的值较大；频率方差是杆绕重心的旋转半径的平方，当重心附近的频谱较大时，频率方差较小，反之，频率方差较大。

表3 频域特征Tab.3 Frequency domain features

通过频域特征可以对滚动轴承的故障进行初步判断，若轴承正常工作，频率成分主要分布在低频，此时重心频率较小；若轴承出现局部损伤，损伤导致的冲击会引起共振，将使主要频率区域向高频方向移动，重心频率和均方频率将增大。

1.1.3 基于小波变换的时频域特征提取

轴承故障的冲击将激发结构的共振，会在振动加速度响应中存在许多共振频带。在这些共振频带中，轴承故障的特征频率将对固有频率进行调制，因此需要对共振频带内的信号进行解调处理以获得故障特征信号。

小波变换具有带通滤波特性，因此被广泛应用于自动提取轴承故障振动加速度信号中的共振频带，再经过包络解调处理得到小波包络谱，最后从小波包络谱中可以提取出轴承故障特征。

设在小波包包络谱中，故障特征频率fd及其各阶倍频附近有特征谱峰存在，设包络频谱分析带宽为fe(通常fe>3max(fd)),包络谱为W(f)，设W(f)谱线的数目为Ne，则包络谱的平均值Sea为

(1)

再令Sed为包络谱中故障特征频率各阶倍频处的谱线平均值，设包络谱中故障频率的谱线数为ne，则

(2)

可构造一个无量纲时频特征

(3)

得到的ΔSe的大小反应小波包络谱中对应故障特征频率处是否存在谱峰。

实际根据轴承转速和几何尺寸计算出的故障特征频率与实际包络频谱中的故障特征频率总是存在差异，通常需要在理论计算的故障频率fd附近小范围内寻找一个最大频谱值作为W(fd)。

在特征量的具体计算过程中，本文采用db8小波对信号进行5层小波分解，可以得到5个细节信号d1，d2，d3，d4，d5和1个近似信号a5。对这6个信号分别进行包络谱分析，通过自动计算可以得到内圈、外圈和滚动体故障所分别对应的3个无量纲特征量，最后求出6个信号中所计算的每个特征量的最大值，作为该特征量值。最终得到分别代表内圈故障、外圈故障和滚动体故障的3个无量纲特征值。

1.2 超球优化方法

在滚动轴承在正常运行过程中，对应的特征向量的空间分布近似呈超椭球状(如多维高斯分布)，因此，本节将在假设多维特征在空间上呈现超椭球状分布的基础上，对超球优化的特征变换方法进行推导。超球优化的思路如下：①旋转超椭球，使其各主轴平行于各坐标轴；②进一步通过尺度变换，使得超椭球状的特征分布在新坐标系中呈超球状分布。

1.2.1 坐标系旋转

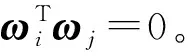
zi=WTyi,W=[ω1,ω2,...,ωd]

(4)

因此问题关键转化为寻找合适的投影矩阵W。

(5)

使用拉格朗日乘子法可得

YYTW=λW

(6)

进一步，通过特征值分解即可得到对应的特征向量ωi。

1.2.2 坐标尺度变换

超球可以看作是超椭球各主轴等长度的特殊情况。通过坐标系旋转，超椭球主轴已平行于坐标轴，此时通过坐标系的尺度变换则可以改变超椭球主轴的长度，在主轴方向实现对超椭球的“拉伸”或“压缩”。主轴的长度反映为方差的大小，因此，令尺度变换后的各维特征的方差为1，可得到空间分布呈现近似超球状的特征向量xi=(xi1,xi2,...,xid)，其中

(7)

(8)

式(7)中分子部分是平移操作，分母部分是尺度操作，得到的xi呈超球心近似位于坐标原点的超球状分布。本文将yi→xi的特征变换过程称为超球优化。

1.2.3 仿真验证

为验证超球所提超球优化方法的有效性，产生了一组二维高斯分布仿真数据(200个样本)，同时给出了相应的高斯描述边界(边界内含97%样本)，如图2所示。

特征分布的复杂度尚无明确的数学定义，但可以根据描述该分布的方程所需参数的多少来衡量。如果一个二维分布的数据边界是椭圆状的，如图2(a)所示，则该分布的边界应以椭圆方程描述最为贴切，一般椭圆方程可以写为Ax2+By2+Cxy+Dx+Ey+D=0，由6个参数确定；如果一个二维分布的数据是正圆状的，那么简单地用圆的方程就可以描述，一般圆的方程(x-a)2+(x-b)2=r2则只需3个参数就能确定。显然，确定3个参数要比确定6个参数更容易。图2直观地给出了二维分布在超球变换前后的结果。通过超球优化后，特征向量的空间分布由超椭球状变换为超球状，使得空间分布的复杂程度降低，这样的超球状分布的特征向量将使得后续分类任务更为容易。

1.3 支持向量数据描述原理

支持向量数据描述能在小样本情况下较好地解决一类分类问题，也被广泛应用于滚动轴承的状态监测与评估。SVDD的目标是寻找包围数据集的最小体积超球，通过解决如下优化问题实现

(9)

式中：l为训练样本数；R为特征空间中的超球半径；C为惩罚系数，ξi为松弛变量；φ(·)为核函数；xi为第i个训练样本对于的d维特征向量；a为特征空间超球球心。

式(9)的对偶表达为

(10)

式中：e=[1, ...,1]T,α=[α1, ...,αl]T；Q为核矩阵，满足

Qi,j=φ(xi)Tφ(xj),∀1≤i,j≤l

(11)

式(10)在形式上与支持向量机的对偶问题一致[17]，因此现存的可用于求解支持向量机的优化方法均适用用于式(10)的求解。

对于未知样本x′，由SVDD得到融合值为

f(x′)=R2+ξi=‖Φ(x′)-a‖2

(12)

根据f(x′)的正负可判断数据点的归类，f(x′)的取值同时能看作是d维特征由SVDD算法得到的一维融合结果。

1.4 超球支持向量数据描述算法流程

所提的超球优化支持向量数据描述算法流程，如图3所示，包括训练和测试2个环节。

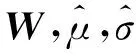
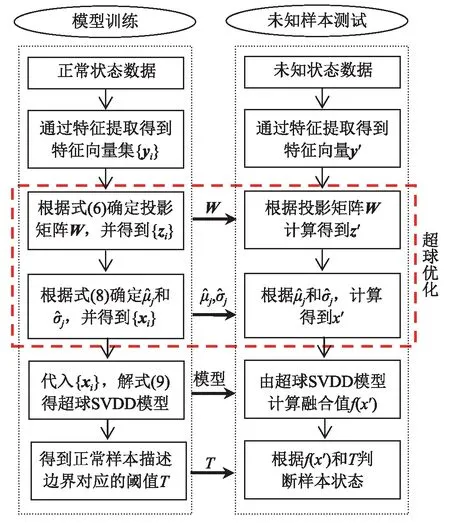
图3 基于超球优化支持向量数据描述的故障诊断流程Fig.3 Fault diagnosis flow chart based on hypersphere optimization SVDD

1.5 性能评价指标

对模型泛化性能进行评估的评价标准就是性能度量[18]。对于滚动轴承故障诊断，最常用的度量指标是错误率，其定义为分类错误的样本数占样本总数的比例。然而，仅通过错误率来度量分类器的性能并不严谨。正如1.3节所述，测试样本输入到训练好的SVDD，SOM和GMM模型中均会产生一个融合值f(x′)，融合值f(x′)将与阈值T进行比较，若f(x′)≤T则轴承状态正常，反之，轴承异常。显然，阈值T的取值将会直接影响分类器的错误率。为避免阈值的选择带来的困扰，基于ROC(Receiver Operating Characteristic)曲线构造了泛化性能评价指标IG，以实现对模型泛化能力的定量评价。

在含二类标记的测试集上，可将测试样本根据真实类别与分类器预测类别的组合划分为真正例NTP、假正例NFP、真反例NTN、假反例NFN，如表4所示。

表4 分类结果混淆矩阵Tab.4 Confusion matrix of classification result

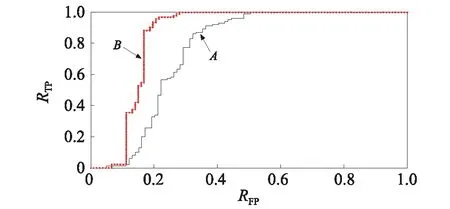
图4 ROC曲线示例Fig.4 An example of ROC curve

于是，定义真正例率RTP=NTP/(NTP+NFN)和假正例率RFP=NFP/(NTN+NFP)。RTP和RFP会随着分类阈值的改变而变化(范围为0～1)，而ROC曲线则可看作由阈值变化而得到的RFP-RTP曲线，如图4所示，ROC曲线的横坐标和纵坐标分别与图1所提及的2类误差相关联。显然，我们希望ROC曲线上的点在RFP较小的时候，RTP尽可能大。如图4所示的ROC曲线中，B基本完全包裹A，可以认为B具有更优的泛化能力。

然而，ROC曲线可能出现交叉现象，此时难以一般性地断言曲线间的优劣。一个较为合理的定量判据是ROC曲线下的面积AUC(Area Under ROC Curve)的大小，记为SAUC。设测试集中有m+个正例和m-个反例，令D+和D-分别表示正、反例的集合，则排序误差Erank为

(13)

式中：∏(·)为指示函数，若·为真则取值为1，反之为0。根据AUC的定义有

SAUC=1-Erank

(14)

因此，我们希望SAUC越大越好。

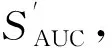
(15)

式中：a为归一化因子，本文取a=0.15，于是IG∈[0,1]。显然IG，越大意味着算法性能越好，对于某融合方法，只要存在一阈值能将2类样本100%正确分类时，该方法对应的IG=100%。

2 试验验证

2.1 试验介绍

为了验证所提方法的有效性，采用沈阳发动机设计研究所研制的带机匣的航空发动机转子试验器进行滚动轴承故障模拟试验[19]，分别在试验器垂直上方和水平方向布置加速度传感器，获取机匣的振动加速度信号，振动信号通过NI USB9234数据采集器进行采集，加速度传感器型号为B & K 4805，采样频率为10.24 kHz，试验器如图5所示。

试验轴承参数如表5所示，采用线切割技术对航空发动机转子试验器涡轮机匣处的6206型球轴承分别进行内圈故障、外圈故障和滚珠故障加工，见图6。分别在1 500 r/min和1 800 r/min下对进行了2组故障模拟试验，试验过程中转速略有波动((20 r/min)。

图5 航空发动机转子试验器Fig.5 Aero-engine rotor tester表5 试验轴承几何参数Tab.5 Geometric parameters of the test bearing

mm

每组试验均从振动监测信号中提取了12维无量纲特征量，时域特征量包括波形因数、峰值指标、冲击指数、歪度、峭度和裕度；频域特征量包括重心频率、频率方差和均方频率；同时，通过小波包络谱自动提取了对应于内圈、外圈和滚动体的3个通频特征量。监测过程中，每个样本包含8 192个数据点，特征量每8 s计算1次，分别从正常轴承和滚动体故障轴承上各获取了110个样本。

2.2 试验结果与方法对比

为验证所提方法的有效性，对不同轴承状态、不同转速、不同测点数据，比较了传统SVDD与超球SVDD的结果。两种方法均采用一半的轴承正常状态样本作为训练样本，另一半轴承正常样本和各类故障样本作为测试样本。文献[11]对比了常用核函数在SVDD的效果，通常径向基核能得到更优的结果，因此，本文中核函数采用径向基核。式(9)中的惩罚系数C、松弛变量ξi以及径向基核中的参数通过三折交叉验证确定。

图7以1 500 r/min机匣垂直测点采集的数据为例，比较了超球优化SVDD与传统方法SVDD在内圈故障、外圈故障和滚珠故障下的ROC曲线。对应的性能评价指标IG如表6所示。

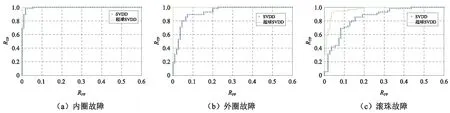
图7 ROC曲线对比(1 500 r/min, 垂直测点)Fig. 7 Comparison of ROC curves (1 500 r/min, vertical test point)

图7(a)中，传统SVDD在对轴承正常状态与内圈故障进行二分类的结果良好，但无论阈值T如何选取，总会有一定的错误率；相比之下，采用所提超球SVDD进行特征融合后，能够找到某一阈值T将两类样本100%正确地分分类。传统SVDD方法在外圈故障(见图7(b))上的效果比内圈故障上较差，但采用所提超球SVDD方法仍能100%正确地实现分类。如图7(c)所示，滚珠故障最难以检测，传统SVDD方法在该组样本上效果很差，而采用所提的超球SVDD方法，故障检测的正确率显著提高。表6则定量的给出了3种故障下各方法的效果。

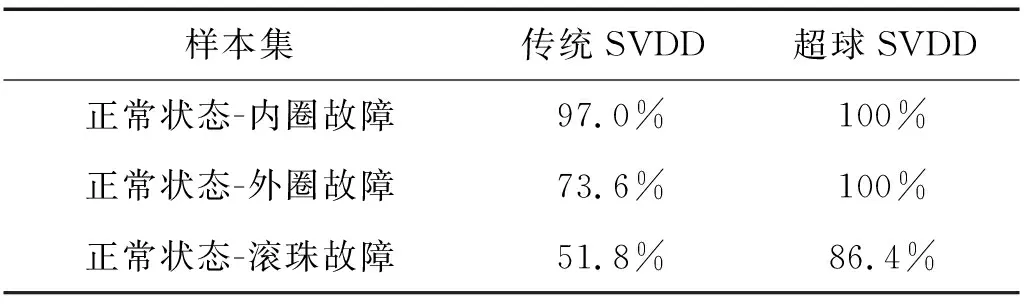
表6 性能评价指标IG (1 500 r/min, 垂直测点)Tab.6 Generalization index IG of different fault types (1 500 r/min, vertical test point)

为验证所提方法性能的鲁棒性，表7比较了不同转速、不同测点下，传统SVDD方法和超球SVDD对滚珠故障检测(考虑到滚珠故障最难以检测)的性能评价指标IG。结果表明，在不同的转速和测点下，所提的超球优化融合方法均具有更优性能。

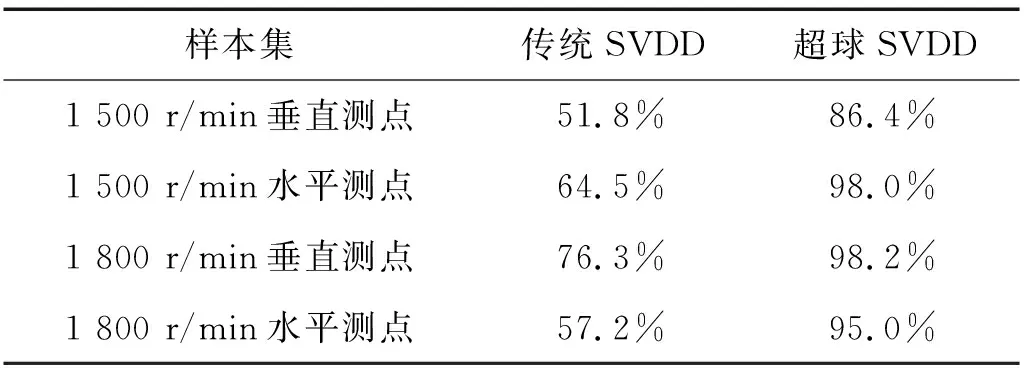
表7 不同转速测点下滚珠故障的性能评价指标IGTab.7 Generalization index IG of ball fault of different speeds and different test points

3 结 论

(1)本文提出了一种超球优化支持向量数据描述的的滚动轴承故障检测方法，通过超球优化改善特征向量的空间分布以降低数据描述任务的难度，进而提升滚动轴承故障检测性能。

(2)多组轴承试验表明，在不同转速、不同测点、不同轴承故障状态下，所提超球SVDD方法相比于传统SVDD方法，故障检测性能显著提高。

(3)本文研究表明，通过改善特征空间分布进而降低特征融合或模式识别任务的难度是可行的，该思想应能推广于其他特征融合方法，如高斯混合模型、自组织特征映射等方法上。