二自由度振子型的二维LR声子晶体弯曲振动带隙研究

吴旭东，张茗海，左曙光，黄海东

(同济大学 新能源汽车工程中心，上海 201804)

近年来声子晶体因为其弹性波带隙特性受到了学者广泛关注，当弹性波频率位于其带隙频率范围之内时，弹性波就不能自由的传播[1]。汽车车身板件振动是车内低频结构噪声的主要来源，因此衰减板件振动成为了车内降噪研究的热点和难点，而声子晶体的相关特性使它在汽车减振降噪方面具有极大的理论价值和应用前景[2]。

目前声子晶体中的带隙可以分为布拉格带隙(频率对应的弹性波波长和晶格常数处于同一数量级[3])和局域共振型带隙(频率所对应的弹性波波长比晶格常数大几个数量级[4])。在结构有限情况下，局域共振带隙可以抑制低频的振动，被广泛应用在杆[5]、梁[6]和板件上[7]。对于元胞中只含单个振子的声子晶体，现有局域共振带隙研究主要集中在单个弹簧型，文献[8-9]等提出了一种周期性排列单弹簧单振子的局域共振声子晶体板，研究了其低频带隙的形成机理和调节方法。文献[10-12]声子晶体中的元胞由单橡胶单振子组成，对其能带结构和对应色散曲线的位移场进行分析，发现局域共振机理可获得更低频的带隙。因此，现有研究仅限于单弹簧单振子基体板的垂向共振模式产生的一个完全带隙[13-14]，尚未考虑到双弹簧类型的声子晶体，这时由于振子转动自由度的增加，会对带隙产生一定影响。

汽车行驶工况下，引起板件振动的激励源往往较为复杂[15]，多频段宽频带的激励特点使其隔振成为一个难题，因此双带隙方面的研究得到了学者的广泛关注。文献[16-17]通过传递矩阵法计算了弹簧并联或串联多个振子的欧拉梁的双带隙，但并联振子获得的低频带隙较窄，而串联振子则使高频带隙变窄。文献[18]则提出了两个橡胶串联两个振子的二维声子晶体，分析了其双带隙的形成机理，进而分析了橡胶和振子的几何参数对带隙的影响，而文献[19]则通过试验证明了并联振子形成的双带隙。因此，现有双带隙的产生需要通过多个弹簧串联或并联多个振子，从而得到多个振子的自由度，由此产生布置高度和振子质量的增加约束了其工程应用价值。如何通过单个振子即可得到目标的双带隙成为研究的难点，而振子的转动自由度的引入则为问题提供解决方法。

针对以上问题，本文设计了一种具有双自由度单振子的局域共振型声子晶体板,与传统多振子串并联型声子晶体相比，通过单个振子的平动和转动相互耦合作用即可形成两个低频的弯曲波带隙。从板件的弯曲振动方程出发，通过平面波展开法计算双带隙范围，而有限元法和样件试验得到的振动传递函数验证了双带隙计算方法的准确性，最后通过对各影响因素的分析为声子晶体在汽车板件多频减振应用上提供参考。

1 双自由度振子型局域共振板带隙计算分析

双自由度振子型局域共振声子晶体板的元胞模型如图1(a)所示，板件通过两弹簧共同连接着振子。其中，具体参数如图1(b)所示，晶格常数为a，板件厚度用h表示，质量为m1；左右弹簧刚度分别用k1和k2表示，其距离板件中心分别为l1和l2；振子质量为m2，其尺寸为b1×b2×h2，转动惯量为J。模型主要考虑对板件声辐射影响较大的垂向振动(z向)，并没有考虑板件的横向位移的影响。

图1 模型参数Fig.1 Model parameters

1.1 平面波展开法带隙计算

根据基尔霍夫薄板理论，板件和振子的运动方程为

(1)

其中,

(2)

式中：w1为板件垂向位移；w2为振子垂向位移；θ为振子扭转振动时绕y轴转过的角度；D=Eh3/12(1-v2)是板件的弯曲刚度；ω为圆频率；f为弹簧对板件或者振子的合力。

根据周期结构的Bloch定理

(3)

同时振子位置的位移满足

(4)

由δ函数的定义求出

(5)

将式(3)～式(5)代入式(1)，整理得到

(6)

选取半轴上M个通过原点的倒格矢，因为G是二维矢量，那么总平面波数量为(2M+1)2，将方程整理成矩阵形式得到

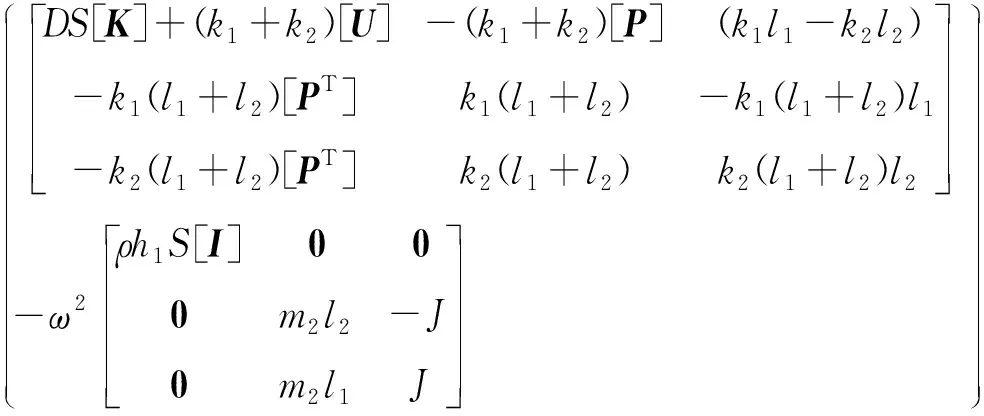
(7)

其中，

至此，方程转为求解矩阵特征值ω2问题，进一步可以求得频率f。将波矢k沿着晶胞不可约Brillouin区的边界进行扫描，将每一个波矢代入方程解出N个特征频率得到声子晶体的能带结构图。

1.2 有限元法带隙特性验证

为了验证平面波展开法计算带隙位置及宽度的正确性，在有限元中建立了8×8 周期的双自由度振子型局域共振板。在有限元模型中，基体板厚度较薄，使用壳单元建模，可以满足仿真的准确性同时减少网格计算时间，而振子需考虑转动惯量的影响因此使用实体建模，振子和基体板则通过弹簧单元连接。在ABAQUS中进行加速度频率响应分析，板件状态为四周自由约束，板件加速度激励信号及响应信号位置如图2所示。

加速度频率响应函数为

(8)

式中：ain为激励信号；aout为拾取振动信号。

双自由度振子型局域共振板参数如下：晶格常数a=50mm，板件厚度h=1 mm；板件和振子材料均为钢，杨氏模量E=210 GPa，泊松比0.3，密度ρ=7 850 kg/m3；左右弹簧刚度为k1=25 000 N/m和k2=25 000 N/m，其距离板件中心l1=0.015 m和l2=0.015 m；振子质量为m2=0.05 kg，其尺寸为b1×b2×h2=40×10×16 mm，转动惯量为7.73 ×10-6kg·m2。

通过MATLAB计算能带结构图如图4(a)所示，选取平面波数量N=(2×5+1)2=121，与相同参数下的单弹簧振子声子晶体对比(见图3)，带隙范围虽然都为153～296 Hz，但双弹簧型声子晶体会在192 Hz处中存在着一条平直带。这平直带类似于二维声子晶体的点或线缺陷结构，此时振动传递函数在带隙范围内有一个局域共振峰。如果将此局域共振峰的频率对应于车身板件的负贡献区频率[20]，可以更有效的实现车内降噪。此时振动加速度频率响应函数如图4(b)所示，带隙范围为154～300 Hz，带隙最大衰减深度达140 dB。同时在180～184 Hz存在一个局域共振峰，局域共振峰带隙频率略小于能带结构平直带，但这与能带结构图中的平直带相呼应，证明计算方法的有效性。

当左右弹簧和中心的距离不等时，即l1=0.015 m和l2=0.01 m，能带结构图如图5(a)所示。此时能带结构图中存在两个分离的带隙，分别为141.7～158.7 Hz，173.4～298.5 Hz。此时加速度频率响应函数如图5(b)所示，带隙频率与能带结构图吻合，带隙内衰减振动可达180 dB。

当左右弹簧刚度不等时，即k1=50 000 N/m和k2=25 000 N/m，能带结构图如图6(a)所示，加速度频率响应函数如图6(b)所示，同样存在两个分离的带隙，分别为165.1～214.3 Hz，248～372.9 Hz。第一带隙宽度相比图5更宽。从图中可以看出，左右弹簧参数不等时，原来的平直带则演变成弯曲的色散曲线，此曲线将原来的带隙一分为二。

因此，振子转动自由度的引入可以增加带隙的数量。工程实际中，往往会出现多个目标减振频率之间大小相差较大的情况，此时单个带隙无法满足大跨度的频率要求，因此可以通过两个不同位置的带隙来解决，充分利用有限的带隙宽度从而达到大频率跨度的减振需求。

图2 有限元仿真板件激振及拾振位置Fig.2 The position of excitation and response in FEM

图3 单弹簧单振子型声子晶体能带结构图Fig.3 The band structure of PCs with single spring and oscillator

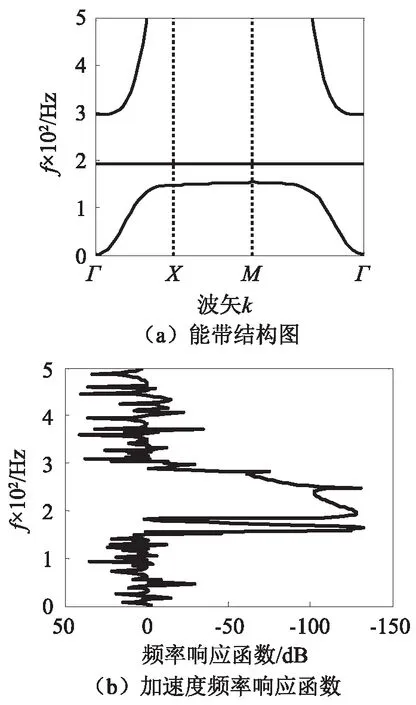
图4 k1=k2且l1=l2Fig.4 k1=k2 and l1=l2

图5 k1=k2且l1≠l2Fig.5 k1=k2 and l1≠l2

图6 k1≠k2且l1=l2Fig.6 k1≠k2 and l1=l2

1.3 带隙样件试验验证

局域共振板参数如下：选取周期数为6×6，晶格常数a=50mm，板件厚度h=1mm；板件和振子材料均为钢，杨氏模量E=210GPa，泊松比0.3，密度ρ=7 850kg/m3；振子质量为m2=0.05kg，尺寸为b1×b2×h2=40×16×10mm，转动惯量为7×10-6kg·m2。经弹簧刚度识别试验得到左右弹簧刚度为k1=46 000N/m和k2=40 000N/m，其距离板件中心l1=0.015m和l2=0.015m。试验样件及设备如图7所示，板件四端通过弹性绳自由悬吊，确保其边界条件与有限元仿真相同，即均处于自由约束状态。测试过程中，为防止弹性绳对激励影响，激振器白噪声激励信号处于板件边缘中点，通过加速度传感器拾取激振点和水平方向边缘点的加速度信号。

图7 样件试验布置图Fig.7 Experiment of flexural vibration in phononic crystals

将获得的激励和响应加速度信号进行计算，得到样件的振动传递函数，将试验结果和有限元仿真结果进行对比，结果如图8所示。对比图中两曲线可以看出，试验得到带隙范围为210～236Hz，250～352Hz，而有限元仿真得到带隙范围为196～252Hz，256～364Hz，这两种方法得到的弯曲振动传递函数基本一致。因此通过试验结果的对比，验证了本文理论计算采用的方法的准确性，同时也验证了双自由度振子型声子晶体能够有效抑制板件振动。

图8 声子晶体弯曲振动传递特性对比Fig.8 Comparison of the flexural vibration transmission spectrums by FEM and experiment

2 带隙机理分析

单弹簧振子型声子晶体带隙形成机理是振子与基体板的垂向共振产生了一个完全带隙，而双弹簧连接时则会出现平直带。因此对带隙的产生进行深入分析，建立带隙开始和截止时对应的简化模型，在带隙开始时，对应的简化模型如图9(a)所示，此时基体板固定不动，对振子多自由度系统分析，建立运动微分方程

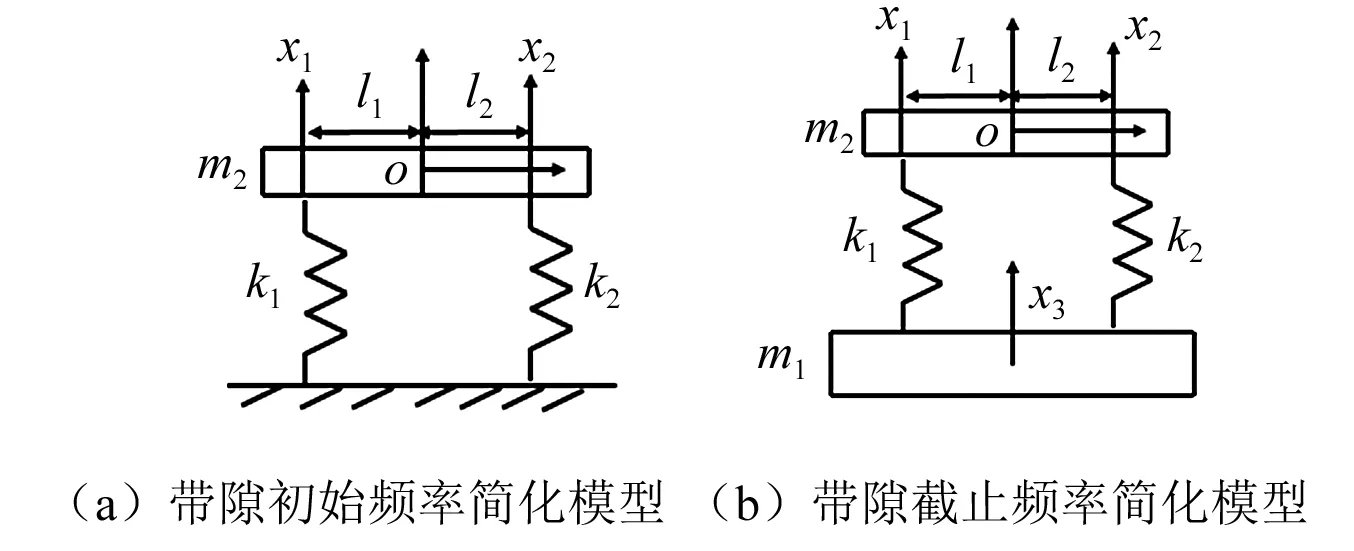
图9 具有局域共振带隙的声子晶体简化模型Fig.9 The simplified model of LR phononic crystals

(9)

刚度矩阵

质量矩阵

在带隙截止时，对应的简化模型如图9(b)所示，此时基体板将与振子共振，运动微分方程为

(10)

通过刚度矩阵、质量矩阵可以求得系统固有频率和主振型，而固有频率即对应带隙开始和截止频率，固有振型则反映了带隙开始和截止时的振动模式。如图10所示，可以看出，采用简化模型和平面波展开法方法计算得到的带隙频率基本吻合，说明该简化模型的有效性，因此可以用该固有振型可以解释带隙的振动模式，即带隙产生及结束的机理。

图10 弹簧刚度对带隙的影响Fig.10 The influence analysis of spring’s stiffness

当左右弹簧参数对称时，带隙开始及结束对应的振型如图11所示，第一带隙开始及第二带隙结束时振子的两弹簧连接点位移相等，振子整体运动为平动，与单弹簧振子型的振动形式相同；而第一带隙结束频率和第二带隙开始频率相等，对应的振型也一样，此时振子绕中心轴转动，板件位移为零，因此正是板件的转动导致能带结构图中出现平直带。

当左右弹簧离中心距离不等或刚度不等时，即l1=0.015m和l2=0.01m或k1=50 000N/m和k2=25 000N/m，其他参数同上不变，通过MATLAB计算得到带隙开始及截止时元胞对应的振型图，如图12所示。当第一带隙开始时，振子以距离中心较远的弹簧或刚度较大的弹簧为轴转动，而第二带隙开始则对应振子以距离较近或刚度较小的弹簧为轴而转动。对带隙结束振型分析，第一带隙截止时，振子转动的同时，中心与板件的平动运动方向相同；第二带隙截止时，振子转动较小，同时振子与板件运动方向相反。因此，振子绕中心轴的转动与垂向平动的耦合导致平直带的产生以及相互分离的双带隙。

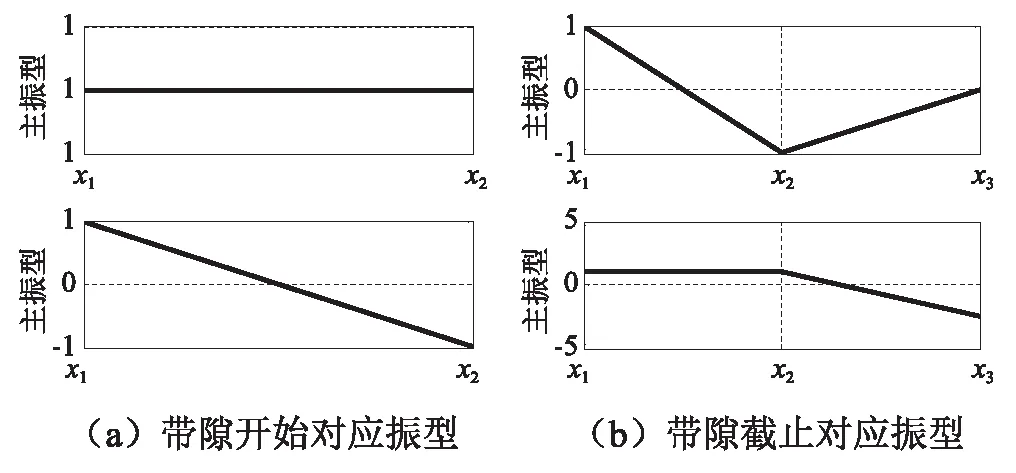
图11 左右弹簧对称带隙开始及截止对应主振型Fig.11 Mode shape when k1=k2 and l1=l2

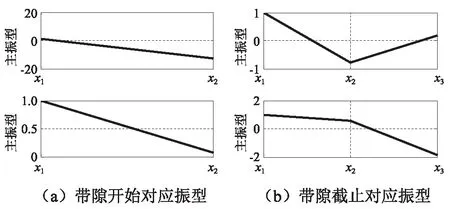
图12 左右弹簧不对称带隙开始及截止对应主振型Fig.12 Mode shape when k1≠k2 or l1≠l2

3 带隙影响因素分析

汽车板件振动激励源往往较为复杂，需要合理选择声子晶体的参数来抑制板件的振动。通过分析声子晶体具体参数对带隙的影响，为双振子型声子晶体在汽车板件的应用提供参考。

3.1 弹簧刚度的影响

如图10(a)所示，保持其他参数不变，左右弹簧距离相等时，当两弹簧刚度增加时，带隙开始、截止以及平直带频率均随刚度增加而增加。当固定一段的弹簧刚度不变(k1=25 000N/m)，改变另一端的弹簧刚度，如图10(b)所示，弹簧刚度增加或减小，均会形成两个分离的带隙。弹簧刚度减小时第一带隙向低频扩展，可以获得较低频的带隙，到一定程度第二带隙基本不变。弹簧刚度增大则向高频移动，到一定程度时第一带隙频率基本不变，而第二带隙继续向高频发展。两弹簧刚度相差越大，双带隙的频率相差也越大。

3.2 弹簧距离的影响

如图13(a)所示，保持其他参数不变，两弹簧刚度相等时，当两弹簧距离同时增加时，带隙的起始和截止频率不受变化，但会影响平直带的频率，平直带的频率基本与左右弹簧距离成正比，要在带隙内形成平直带的缺陷态效果左右弹簧距离需要满足一定的条件，否则平直带均在带隙外。当固定其中一弹簧距离不变(l1=15mm)，改变另一弹簧距离，如图13(b)所示。第一带隙截止频率与弹簧距离成正比的关系，两弹簧距离相等后，第一带隙起始频率随距离变化很小。而第二带隙则正好相反，起始频率在前10mm随距离减小而后成正比的增加，而截止频率则较为平缓，两弹簧距离相等前减小而之后增加。

3.3 振子质量和转动惯量的影响

如图14(a)所示，当弹簧左右参数对称时，此时带隙开始及截止振动模式均为振子的平动，因此转动惯量对带隙起始及截止频率均无影响。转动惯量只会改变平直带对应的频率，转动惯量越大，平直带对应频率越低。因此转动惯量在一定范围内，带隙内才有局域共振峰出现。但当左右参数不对称，例如当左右弹簧距离不等时，如图14(b)所示，转动惯量越大则第二带隙带宽越大，反之则第一带隙带宽越大；且随着转动惯量越大，第一带隙向低频移动。

图13 弹簧距离对带隙的影响Fig.13 The influence analysis of spring’s distance

由图15(a)所示，当系统左右参数对称时，因为此时带隙开始和截止时振子的振动模式是振子绕中心轴转动，与纯质量无关，质量对平直带对应的频率没影响，质量越大带隙越往低频走，与单弹簧振子带隙趋势相同。但当左右参数不对称，例如当左右弹簧距离不等，如图15(b)所示，质量增大，第一带隙截止频率基本不变，开始频率向低频移动；到达一定范围时，第二带隙起始频率变化较小，截止频率相比开始频率变化较大。

图14 振子转动惯量对带隙的影响Fig.14 The influence analysis of oscillator’s moment of inertia

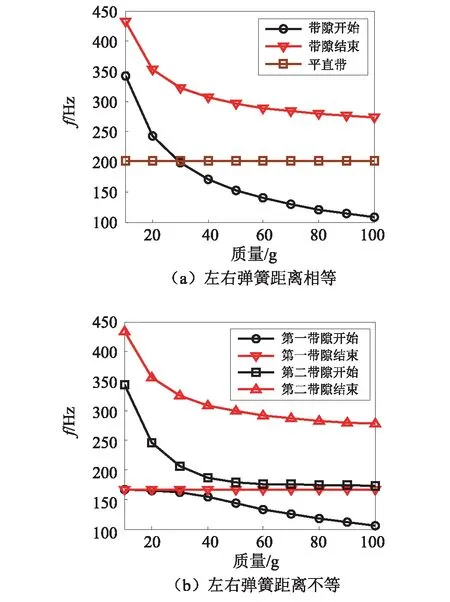
图15 振子质量对带隙的影响Fig.15 The influence analysis of oscillator’s mass

4 结 论

针对汽车行驶中多频段宽频带的激励源特点，为抑制板件的低频振动，本文提出了一种单振子双弹簧类型的二维声子晶体结构，使振子具有平动和转动的自由度，计算并分析了其双带隙特性，并得到以下主要结论：

(1)平面波展开法计算了二自由度振子型声子晶体的色散曲线，并通过有限元法和样件试验的振动传递特性进行验证。与传统单弹簧振子型声子晶体相比，双弹簧声子晶体能带结构图中带隙内会出现一条平直带，类似缺陷态特性，使加速度频率响应函数带隙内中出现局域共振峰；当双弹簧参数非对称时，平直带拓宽，使能带结构中产生明显分离的双带隙。

(2)从带隙开始和截止频率对应的振型可以得到，当第一带隙开始时，振子主要以距离中心较远的弹簧或刚度较大的弹簧为轴而转动，而第二带隙开始则对应振子以距离较近的弹簧为轴或刚度较小而转动。因此，振子的转动与垂向平动的耦合导致平直带的产生以及相互分离的双带隙。

(3)弹簧刚度和距离的不等分布有助于双带隙的产生。距离、刚度越小有助于第一带隙向低频移动，越大则第二带隙向高频移动；振子质量越大，第一带隙越宽频率越低，而转动惯量越小则第一带隙越宽，但频率也越高。通过调节四个参数的数值可以得到特定的双带隙范围，为声子晶体在汽车板件多频减振应用中提供了新的设计方法。