考虑非线性电磁分布力的虚拟电动振动系统建模

左曙光，黄荣奎，冯朝阳，吴承喜

(同济大学 新能源汽车工程中心，上海 201804)

在汽车行驶过程中，汽车零部件会承受由路面不平度激励引起的振动，对其可靠性、耐久性与使用寿命有较大影响[1]。在其研发过程中，一般通过振动台试验来复现汽车零部件在真实运行工况下所受到的振动环境，以考察其可靠性。但振动台试验需要制造出零部件样品以及配套的工装，周期长且耗费大；另一方面，由于传感器数量以及安装位置受到限制，难以全面地观测试验结果。针对以上两点，结合有限元方法与试验方法的优点构建一套虚拟电动振动系统，有助于在研发过程中对零部件预先验证与不断优化，实现关键零部件的动态设计，可有效避免试错设计方法造成的损失。

电动振动台是振动环境试验的主设备，构建虚拟电动振动系统的研究也颇多。范宣华等[2]建立了动圈有限元模型，利用附加边界条件的方式来代替整个振动台模型，并用该模型完成了对试件随机振动试验进行了仿真；宋琼等[3]建立了动圈、夹具、试件一体化的有限元模型并辨识出其传递特性，通过Matlab平台联合振动台传递函数和控制器构建了闭环的虚拟振动试验系统；谭永华等[4]将振动台刚体模型、数学模型与夹具有限元模型相结合，利用Matlab/simulink软件环境建立了闭环振动试验仿真系统；以上主要是进行对振动台动圈建模与相应振动仿真，但忽略了动圈与磁场之间的耦合效应；另一种是基于多体动力学和机电耦合仿真的闭环建模[5-7]，但目前的研究把电磁力等效为一个简单的集中力，不能反映动圈的真实受力情况及其空间分布；此外，对于从理论上推导电磁力的分布规律的研究者甚少，从电磁场的角度去分析电磁力分布规律有待进一步的研究。

为了考虑了动圈和磁场的耦合效应，反映动圈在运动过程中的真实受力情况，本文首先建立振动台电磁解析模型，从理论上研究了驱动线圈在运动过程中所受电磁力的分布规律；然后建立了磁路有限元模型和动圈电学模型对电磁场进行有限元仿真，仿真结果与理论分析进行了验证；最后在有限元中耦合了磁路有限元模型、动圈电学模型以及动圈结构模型，形成了一套完整的虚拟电动振动系统。理论分析以及利用JMAG软件对动圈在运动过程中受到的电磁驱动分布力进行提取发现，电磁力并非一个简单的等效集中力，它是分布力而且其大小不仅与电流有关，还跟动圈运动位置有关。此外，本文基于电磁分析与结构模态分析的仿真结果，在Virtual.Lab软件中运用瞬态模态叠加法来求取加速度响应，从而实现对动圈上任意一点的振动响应的实时观测。最后，利用该虚拟振动系统进行了空台正弦振动试验，并与传统线性模型进行对比，该虚拟振动系统仿真结果表明，台面加速度响应出现谐波失真的现象，可以得出结论，非线性电磁力是导致的振动响应失真的重要原因之一。

1 电动振动台运行原理

电动振动台主要由励磁线圈，双磁路磁钢结构，中心磁极，驱动线圈，筋板，台面等构成，其结构如图1所示。其中，驱动线圈，筋板以及台面构成的系统称之为动圈。电动振动台是根据电磁感应原理设计的，振动台的驱动线圈处于一个高磁感应强度的工作气隙中，当驱动信号由控制器产生并经功率放大器放大后，加载到驱动线圈上，振动台就会产生需要的振动波形。

对于大型电动振动台，它的磁场是由大电流励磁线圈激发的，由于磁路结构的不对称性以及动圈交变磁场和励磁磁场的相互作用，导致很难形成均匀且恒定的工作气隙磁场，这就导致所产生驱动力的非线性与不均匀性，从而导致了振动台的振动响应出现谐波失真现象[8-9]。由此可知，我们需要对电磁系统进行解析建模以及有限元建模，以反映振动台动圈的实际受力情况。

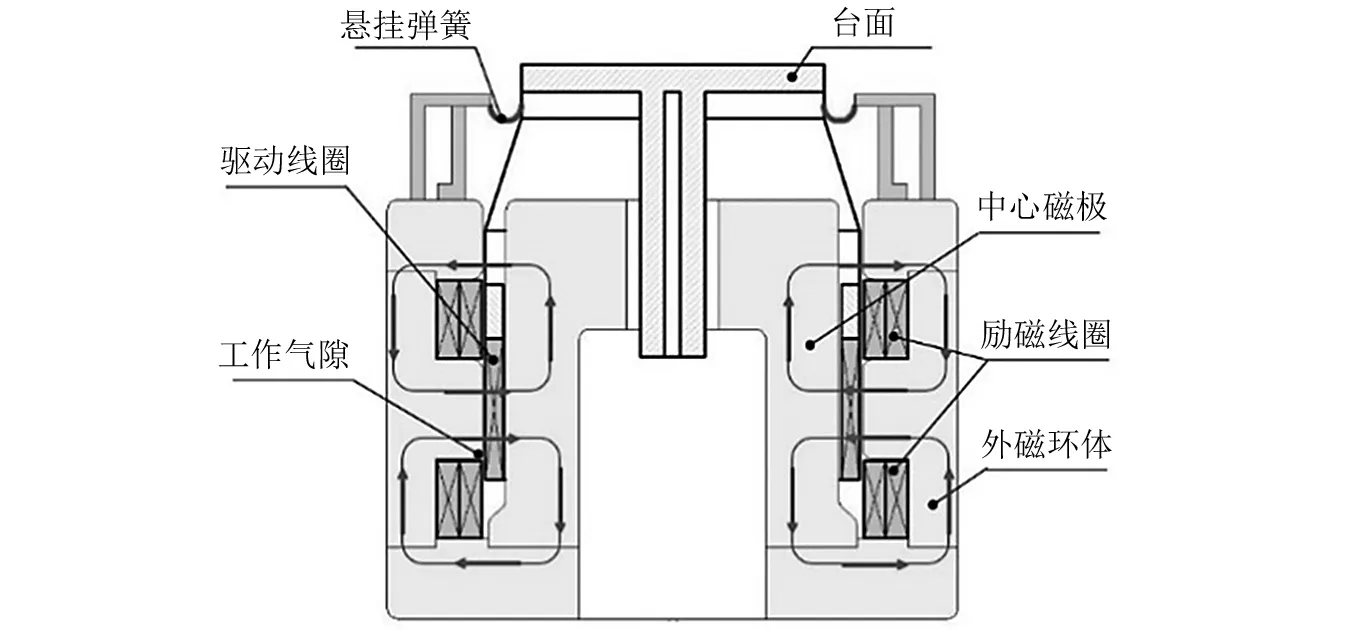
图1 电动振动台结构示意图Fig.1 Electric shaker structure schematic

2 非线性电磁分布力理论分析

由于振动台具有左右对称的磁路结构，这里以右半边磁路结构来分析电磁力的分布规律。驱动线圈处于平衡位置时，电动振动台磁路结构的磁力线分布情况与磁感应强度分布，如图2所示。从图中可以看出，磁路以工作气隙中心处为分界，主要分为围绕上下励磁线圈的两部分，有四处区域磁感应强度达到2T以上，磁饱和程度较高。

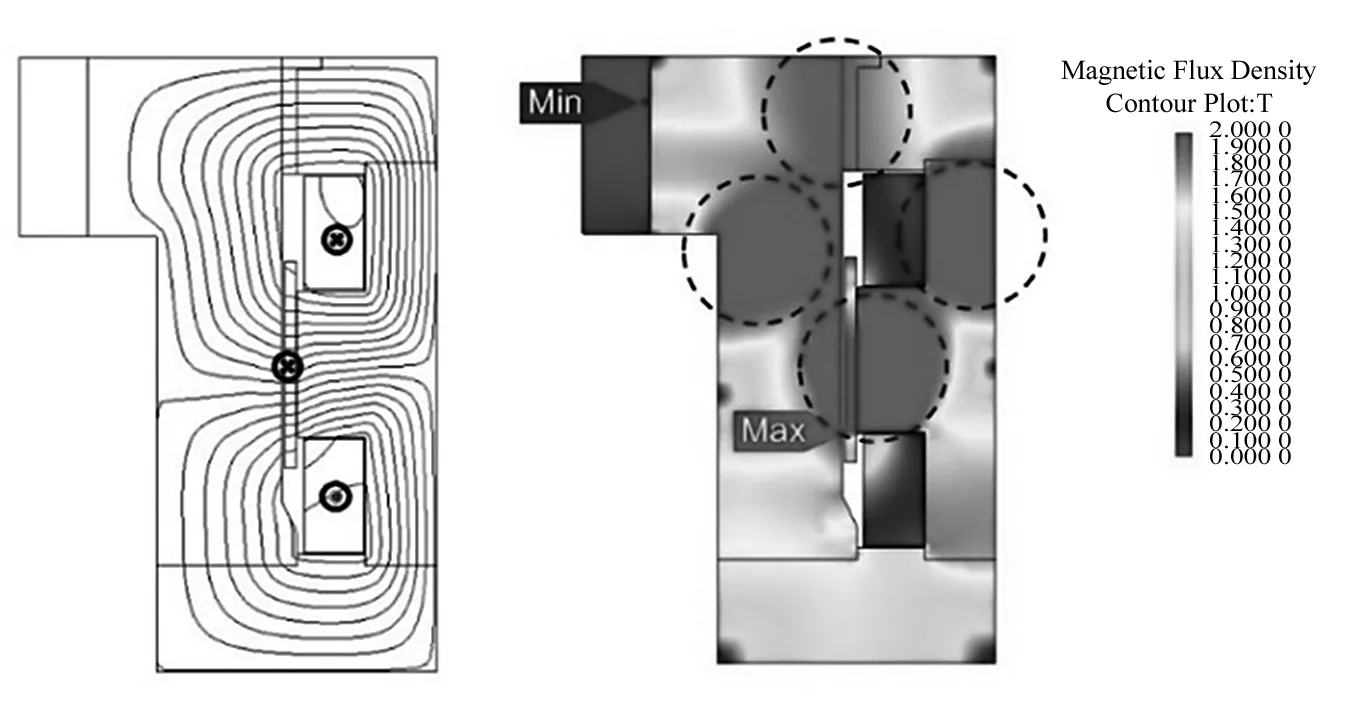
图2 磁路结构磁力线分布与磁感应强度分布Fig.2 Magnetic field distribution and magnetic flux density distribution of magnetic circuit structure

基于磁动势乘磁导的方法，实际上是微分化的磁路等效法，应用磁通管法的思想，单独对每条磁路进行研究。先建立随空间分布的磁动势方程，再将磁力线近似看作圆弧或直线来模拟磁力线在气隙中的路径来求取气隙的磁导[10]，磁密计算公式为

Br=Fm×Λm

(1)

由式(1)可知，气隙中某一点的径向磁感应强度主要由通过该点的磁路磁动势与磁路磁导决定，要想精确计算其径向磁感应强度，就需要建立考虑驱动线圈运动位置的磁路磁动势与考虑磁钢磁饱的磁路磁导的空间分布方程。

针对动圈处于平衡位置且通正向电流的情况，工作气隙中某一点距离气隙中心距离为z，对该点展开磁路建模分析。

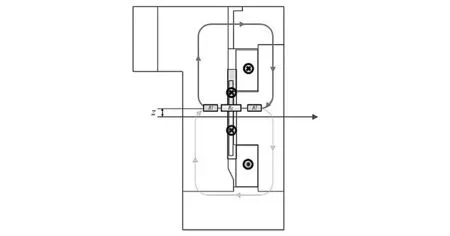
图3 磁路磁动势分析图Fig.3 Magnetic circuit magnetomotive force analysis diagram

由图3可以看出，磁路磁动势由励磁线圈磁动势与驱动线圈磁动势叠加而成，考虑驱动线圈上z上下的磁动势分别对原磁场的加强与削弱作用，其在气隙中的空间分布可表达为

(2)

式中：N，Nc分别为励磁线圈与驱动线圈的匝数；I，Ic分别为励磁线圈与驱动线圈的通电电流大小；hc为驱动线圈高度，z为该点到工作气隙中心点的距离。

进一步考虑驱动线圈的位移s，则有

(3)

化简后得

(4)

(5)

磁路磁导主由气隙磁导与磁钢结构的等效磁导两部分组成。磁导的基本计算公式为

(6)

式中：g为气隙中磁力线长度；μ0为空气磁导率，其值为1.26×10-6；l为磁钢中磁力线等效长度；μd为磁钢结构动态磁导率。

观察图2可知在主要工作气隙内，气隙中磁力线长度和磁钢中磁力线长度均与气隙高度相关。动态磁导率除了与气隙高度相关外，还与驱动线圈通入电流大小有关，因此气隙中磁路磁导空间分布的计算公式

(7)

综上，根据式(1)，可以得出气隙中的磁密分布与驱动线圈电流以及气隙高度有关，进而反映出动圈运动过程所受的电磁力不仅与驱动线圈通入电流有关，还与动圈运动位置有关，即电磁力为空间分布力。为了进一步论证该理论推导，接下来对某电动振动系统进行了建模以及仿真研究。

3 电动振动系统建模

3.1 电磁系统建模

大型电动振动台的磁路系统包括励磁线圈、双磁路磁钢结构、中心磁极以及工作气隙。工作时，上下励磁线圈通以方向相反的直流电，并由磁环体、中心磁极与上下磁钢盖引导磁力线在磁钢中部处叠加，从而使工作气隙磁场最强。

本文以某12 t推力电动振动台为例，用JMAG软件进行磁路结构有限元建模。磁钢结构与中心磁极，材料设置为十号钢，沿周向对中心磁极开8道槽，为动圈预留装配空间。分别给上下励磁线圈加载方向相反的180 A直流电，匝数为350匝，材料设置为铜，磁路系统有限元模型如图4所示。

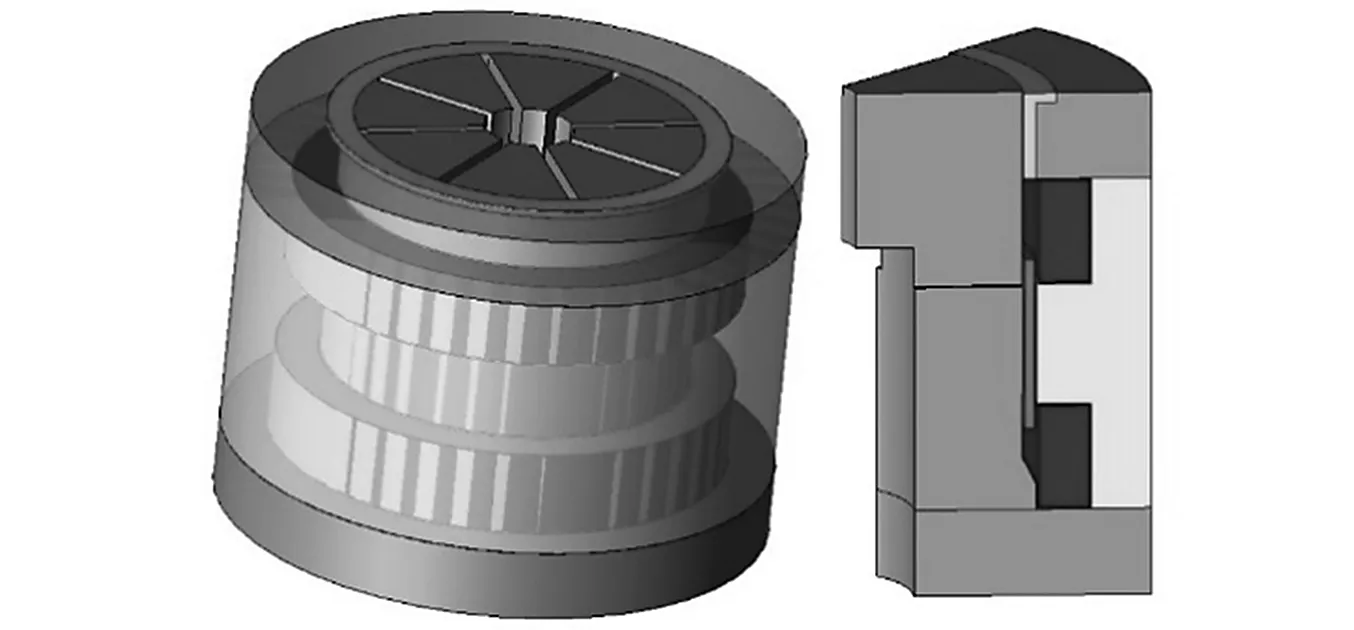
图4 磁路系统有限元模型Fig.4 Finite element model of magnetic circuit

电磁力一般由公式F=BLI计算，其中BL为电磁力系数，电磁力大小与通电电流大小成正比。但实际运行过程中，电磁力系数会随着驱动线圈运动位置的改变而改变。同时随着通电电流的增大，驱动线圈引起的磁动势对原有励磁磁场的影响加剧，导致电磁力系数随位置变化更为显著。为测取电磁力系数-位置曲线，驱动线圈匝数设为70匝，材料设置为铜，分别通以大小或者方向不同的直流电，让动圈从工作行程下止点(-38 mm)运动到上止点(+38 mm)。

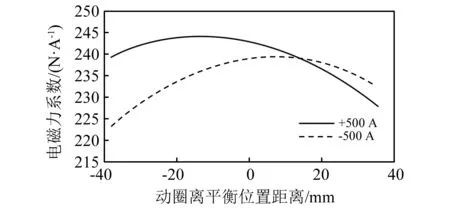
图5 电磁力系数-位置曲线Fig.5 Electromagnetic force factor-position curve

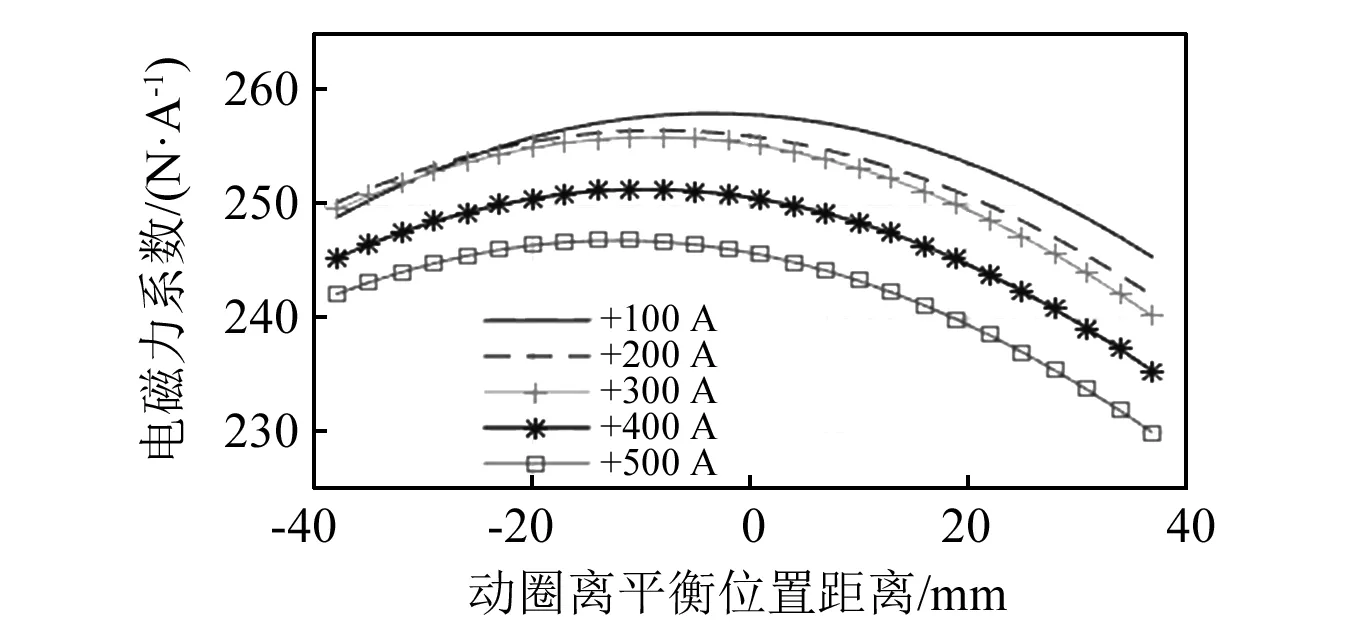
图6 不同电流大小电磁力系数-位置曲线Fig.6 Electromagnetic force coefficient of different current size-position curve

如图5所示，大电流工况下，动圈的电磁力系数会随着其运动位置的改变而发生比较显著的变化，最大可相差8.1%。通反向电流时，电磁力系数曲线峰值向工作行程上半段偏移，且整体数值减小约5 N/A。结合图6，说明了电磁力系数变化规律不仅与动圈运动位置有关，也与电流大小和方向有关。以上仿真结果对理论分析的结论进行了很好的验证。

为了反映驱动线圈在运动过程中真实受力情况，图7为仿真过程中某一时刻，驱动线圈所受的电磁力分布图，驱动线圈主体受力为垂直轴向力，在两端所受电磁力包含一定的径向分量。电磁力系数-位置曲线呈现出的非线性与动圈受力的不均匀性，验证了对电磁系统进行深入研究并将之运用于虚拟电动振动系统的必要性。

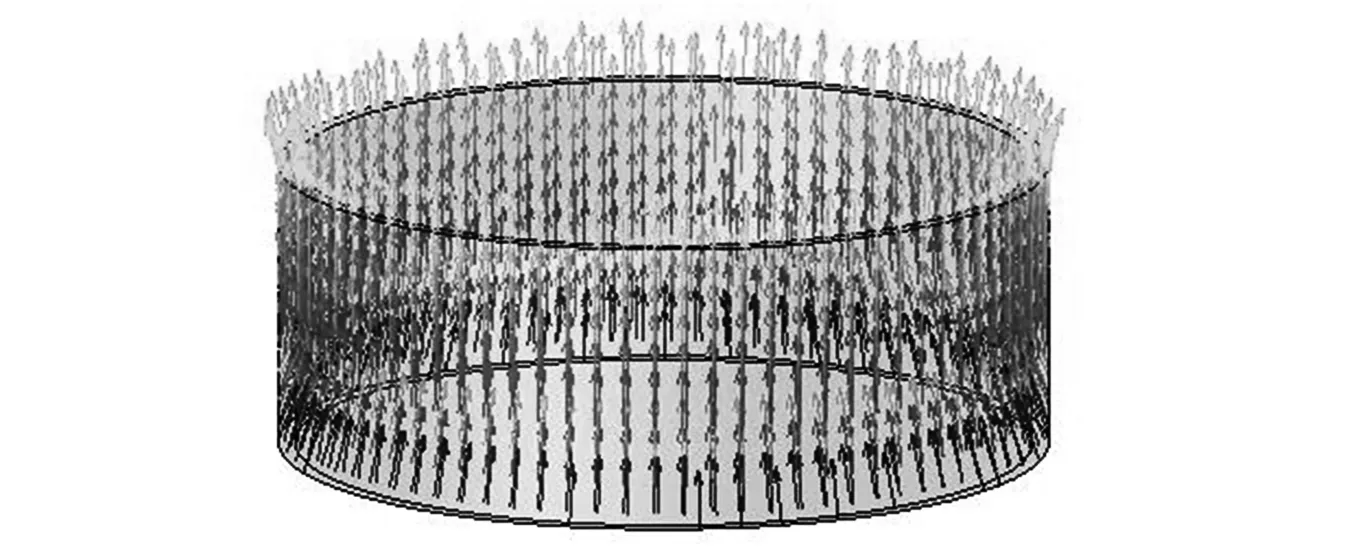
图7 动圈受力分布图Fig.7 Force distribution map of moving coil

3.2 动圈结构建模

为研究电动振动台台面振动特性，需对其运动部件动圈进行结构有限元建模。电动振动台动圈主要结构如图8所示，主要由台面，骨架，绕线壁筒，驱动线圈等组成。本文分析的动圈基本结构参数：台面直径560 mm，总高度700 mm，质量100 kg。动圈骨架、台面与绕线壁筒由铝合金整体浇筑而成，线圈绕在铝合金绕线壁筒上，环氧树脂与最外层不锈钢钢片用于黏结、固定线圈[11]。考虑建模与网格划分的方便性，在建模过程中将线圈、壁筒、环氧树脂以及钢片等效为单一实体，作为动圈驱动部分，同时对台面与动圈骨架整体建模，为骨架部分。在材料定义过程中，驱动线圈部分以环氧树脂为主，同时考虑铜和钢的材料参数[12]。最终动圈的参数修正值为：骨架部分弹性模量E=88.5 GPa，密度ρ=2 520 kg/m3；驱动线圈部分弹性模量E=90 GPa，密度ρ=2 600 kg/m3；建模过程忽略螺纹，螺栓，倒角等因素的影响。

实际振动台台面周向每隔90°布置一个钢片弹簧，以限制动圈台面的横向摆动和转动。安装在动圈中心孔内的中心导杆也能起到限制动圈横向摆动的作用。动圈通过中心导杆与下部的空气弹簧相连接，空气弹簧可根据被测件质量来灵活调节动圈的平衡位置以及提供轴向支撑刚度。为使模型的边界条件与实际情况等效，钢片弹簧和中心导杆的作用采用20个均布弹簧代替；空气弹簧用弹簧单元等效，刚度设置为2.088×106 N/m，阻尼系数设置为2×105 N·s/m。其中空气弹簧刚度和阻尼是通过振动台工作频率下限值计算得出。动圈的边界条件整体施加情况如图9所示。

图8 动圈结构示意图Fig.8 Structure of moving coil

图9 边界条件Fig.9 Boundary conditions

为了验证构建的动圈有限元模型的有效性，对空台振动台动圈进行了模态试验测试。由于动圈骨架安装在台体中，只有台面部分可以进行试验操作，因此所有传感器都布置在台面上，以辨识出动圈的各阶模态。台面上的加速度传感器布置示意图如图10所示，均为三向加速度传感器，以便能够测取多方向更精准的振型。

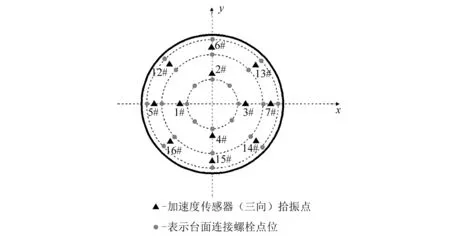
图10 台面测点布置示意图Fig.10 Layout of measuring points on the table

由于数据采集系统的通道数与传感器数量的限制，每次试验只能布置7个传感器，如图11所示。每组试验依此测取1～7号、8～14号、15～16号拾振点的加速度响应。

由于电动振动台动圈除了存在典型的轴向伸缩模态，还存在许多其他类型的模态，比如扭转模态[13]、摆动模态[14]、台面局部变形模态等，这些也会对电动振动台的工作性能产生一定程度的影响。因此激振点的位置和方向的选择要考虑激发出这些模态特征。激振点的布置如表1所示。

图11 台面传感器现场布置图Fig.11 Layout of sensors on the table表1 激振点坐标与激振方向Tab.1 Excitation point coordinates and excitation directions

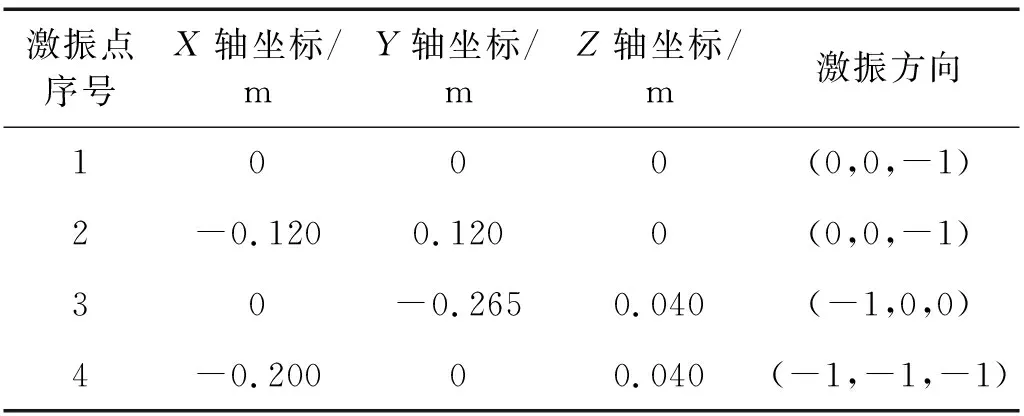
激振点序号X轴坐标/mY轴坐标/mZ轴坐标/m激振方向1000(0,0,-1)2-0.1200.1200(0,0,-1)30-0.2650.040(-1,0,0)4-0.20000.040(-1,-1,-1)

模态试验结果和仿真结果的对比如表2所示，误差基本控制在7 %以内，证明构建的有限元模型有效。

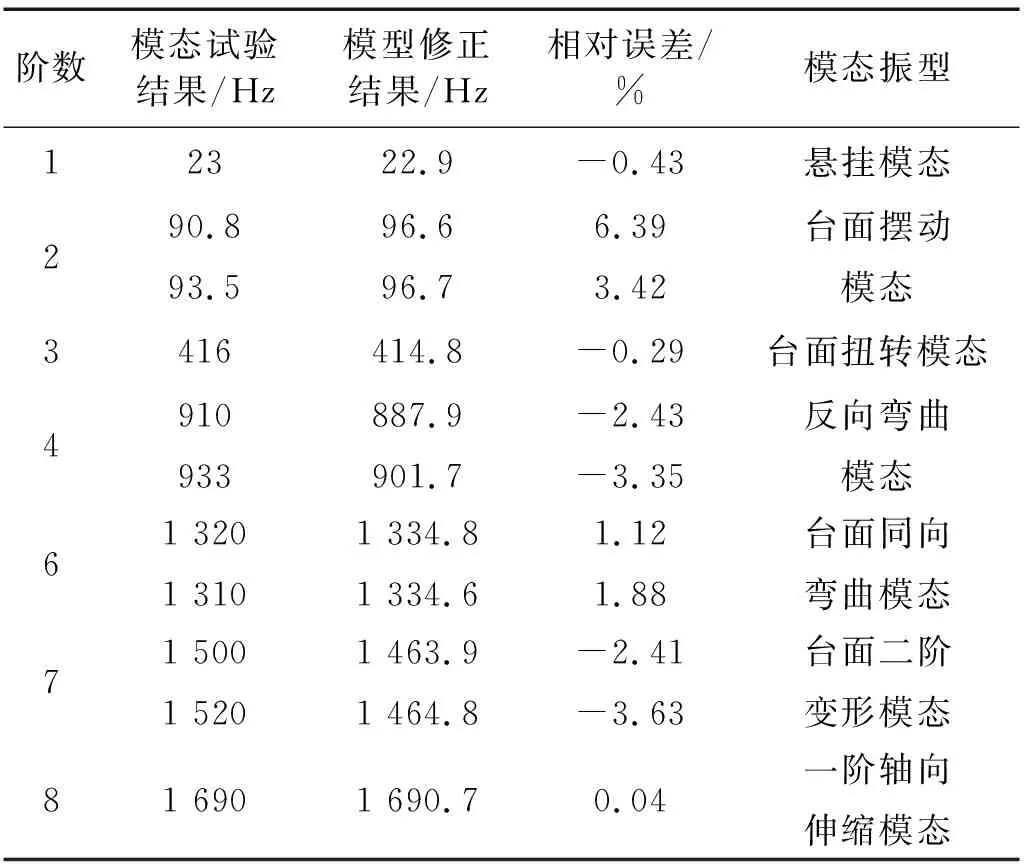
表2 模态试验和仿真对比Tab.2 Modal test and simulation comparison

4 电磁-结构耦合仿真

如前文所述，工作气隙中的磁场是非均布的，而且会受到驱动线圈的电流大小以及运动位置的影响，使动圈所受电磁力呈现出一定的非线性与不均匀性。在现有的电动振动台虚拟仿真研究中，动圈驱动力的加载是均匀的，或者只是简单地等效成一个面集中力，与实际的受力情况有较大的差异，并不能反映动圈的真实受力情况。

电磁-结构耦合仿真是指在有限元分析过程中，考虑电磁场与结构场的交叉作用和相互作用。本文运用顺序耦合的建模方法，先通过电磁有限元模型计算出驱动线圈时域分布电磁力，导出结果节点力文件，同时在Virtual.Lab中导入由结构模型得到的动圈模态分析结果，然后把电磁力映射到结构网格上，作为振动仿真的输入，最终可实现时域振动响应输出。较现有学者的等效电磁力，可以更准确反映动圈的受力特点和台面结构振动响应。其流程框图如图12所示。

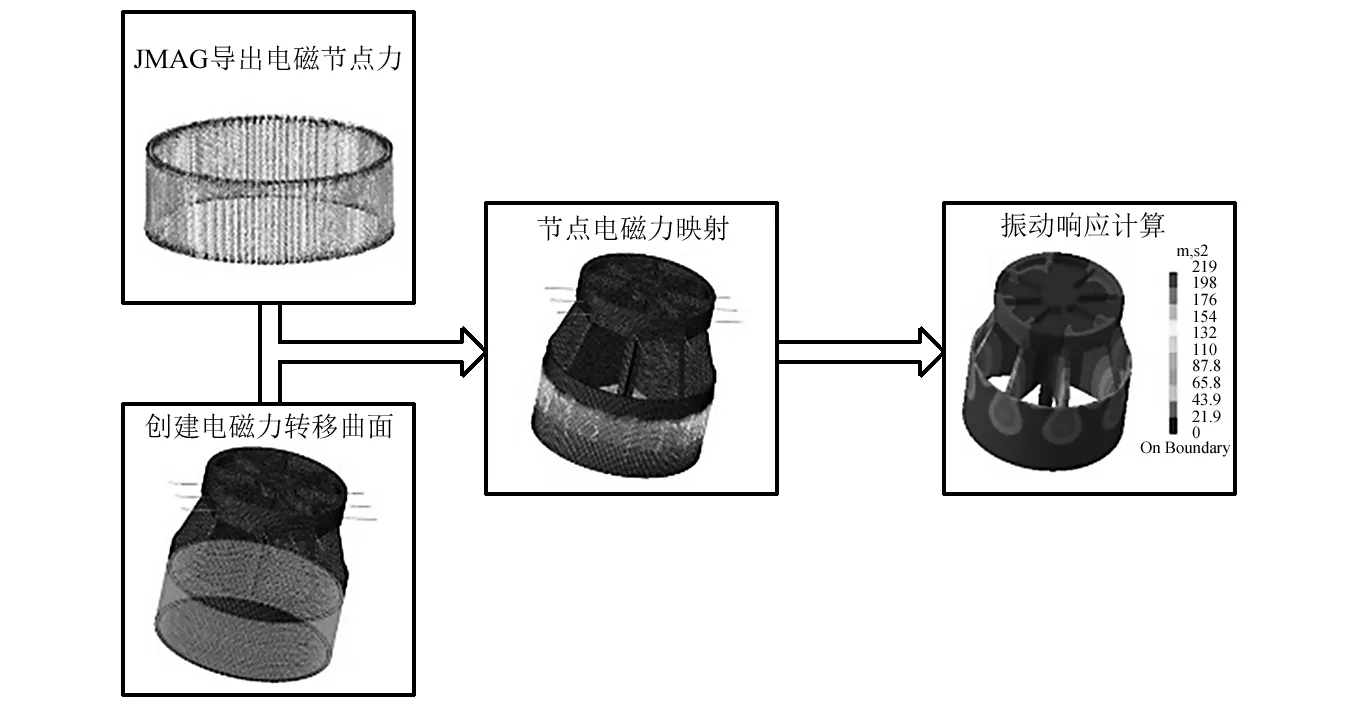
图12 电磁-结构耦合仿真流程图Fig.12 Electromagnetic-structural coupling simulation flow chart

JMAG软件中的电磁仿真为瞬态分析，导出的电磁力信号为时域信号，故在Virtual.Lab软件中使用瞬态模态叠加法进行空台状态下的动圈台面振动响应的计算，时间步长和步数与电磁仿真设置相同。通过这样一套耦合仿真流程，可以得到考虑电磁非线性与不均匀性的台面振动响应，结合有限元模态分析，可对台面上任意一点的加速度值进行观测。

5 应用实例

为验证所构建虚拟振动系统的实用性，本文进行了某一频率下的空台正弦振动试验。给驱动线圈加载幅值为400 A，频率为40 Hz的正弦电流输入，进行瞬态电磁仿真计算得到驱动线圈受到的空间分布电磁力,然后将该电磁分布力映射到Virtual.Lab仿真环境下的动圈上进行耦合振动仿真，得到台面中心点向加速度输出曲线，如图13所示。

图13 动圈台面中心点Z向加速度响应曲线Fig.13 Z-axis acceleration response curve of center of moving coil table center

由仿真结果可看出，台面中心点的加速度波形发生了一定程度的失真。为量化其失真程度，对加速度输出信号进行谐波分析。分析结果如图14所示，加速度输出信号基频为40 Hz，其整体谐波失真度为2.12%，主要由0阶(直流偏移)、0.5阶(直流偏移)、2阶、3阶、4阶的谐波分量引起。

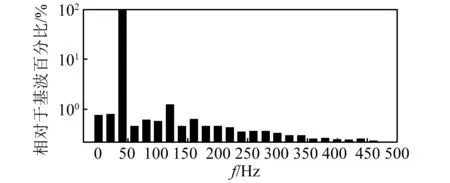
图14 动圈台面中心点加速度谐波分析图Fig.14 Harmonic analysis of acceleration of center of moving coil table

根据现有研究中的线性电磁力模型

F=Blni=Ki

(8)

式中：B为磁场强度T；l为单匝线圈的长度m；n为线圈匝数；i为驱动线圈中流过的电流。理论上认为F与i之间表现为线性关系，且比例参数记为K。那么在正弦电流激励信号下，输出的电磁驱动力也是标准的正弦信号。依据本振动台提供的气隙中磁场强度等效值，对于400 A，频率40 Hz的正弦交流电输入，理论电磁力为幅值9×104 N，频率40 Hz的正弦输出(见图15)。

图15 动圈所受Z向驱动力仿真值与理论值对比图Fig.15 Compare Z-axis driven force computed by the simulation with theoretical value

但由于工作气隙磁感应强度分布的不均匀性，实际驱动力信号会出现一定程度的波形失真。为分析振动加速度信号谐波失真出现的原因，对动圈在运动过程中受到的电磁力进行了提取分析，并与线性模型的计算结果作对比(见图15)，可看出实际驱动力峰值比线性模型计算峰值大约11.1%(见图16)，且出现一定程度的波形失真。动圈运动过程中驱动力的失真，说明了驱动力和电流不是简单的线性关系。为此提取了在动圈从下止点运动到上止点过程中电磁力系数的变化规律，从图17可以看出，电磁力系数和电流的方向以及动圈运动位置有关并且呈现非线性的关系。以上说明了在动圈运动过程中，电磁力与位置的非线性关系导致了其加速度出现了谐波失真。

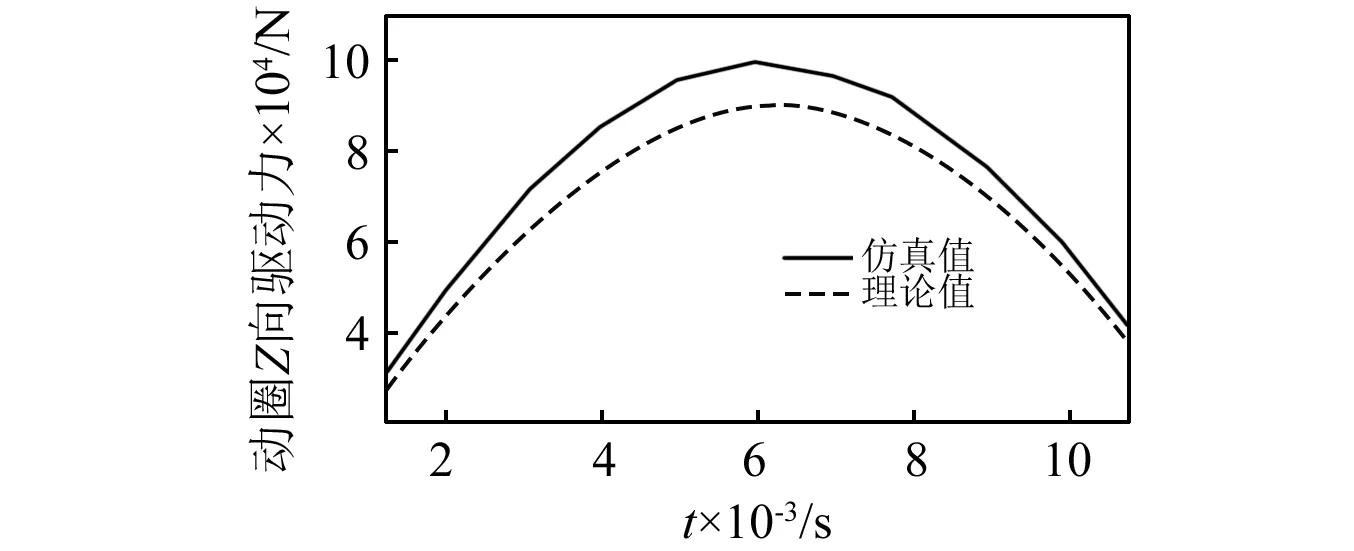
图16 图15中第一个波峰处局部放大图Fig.16 Magnified view of the first peak ofFig.15

图17 电磁力系数-位置曲线Fig.17 Electromagnetic force coefficient-position curve

为了从微观观测驱动线圈表面电磁力分布的不均匀性，在驱动线圈上取三个等距离节点，从上到下三个节点编号分别为16 012，16 315，16 618。该三个节点的驱动力-时间曲线如图18所示，从中可知不同高度位置的三个节点在运动过程中受到的驱动力幅值相差较大。反映了动圈运动过程中驱动线圈表面电磁力并非均布力。

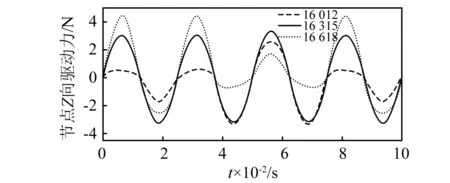
图18 驱动线圈上不同高度的三个节点驱动力曲线Fig.18 Drive force response curve of three different nodes on the driving coil

通过电磁-结构耦合分析，发现在低频率大位移工况下，振动台台面的加速度输出出现一定程度的谐波失真。通过对电磁力的提取可以发现，在动圈的运动过程中，气隙中的磁场分布呈现不均匀性导致了电磁力的非线性特征。因此，本文所构建的考虑电磁非线性的虚拟电动振动系统更能够反映电动振动系统在工作过程中呈现出的非线性真实特性，具有较强的实际意义。

6 结 论

本文建立了磁路有限元模型、动圈结构模型、动圈电学模型并将其耦合，形成一套完整的虚拟电动振动系统。对电磁驱动力分布规律及其对台面运动响应的影响进行了深入研究。该虚拟振动系统考虑了动圈和励磁磁场的耦合效应，此外，台面任意时刻、任意位置的振动响应都能被观测到，可为真实振动台试验提供预试验。通过建立该模型，可以得到如下结论：

(1)动圈驱动线圈所受的电磁力空间非均匀性和位置相关性。由于磁路结构局限性造成的工作气隙磁场分布不均匀，导致了驱动线圈所受的空间电磁力具有非均匀分布特性，同时也导致动圈在垂向运动过程中总体的电磁力系数也与位置具有相关性。

(2)驱动线圈所受的电磁力与电流的相关性。由于动圈电流产生的磁场与原励磁磁场的相互作用，以及磁路上下不对称结构的影响，动圈的总体电磁力系数与其驱动电流的大小以及方向有关，在大电流情况下，结合结论(1)，总体的电磁力更容易受垂向位置的影响，呈非线性的关系。

(3)仿真实例可以发现，由于动圈在运动过程中受到非线性电磁力，结合动圈的模态特性，导致动圈台面的实际加速度响应呈现一定程度的谐波失真，从而说明了非线性电磁力是导致的振动响应失真的重要原因之一。