基于半径差约束最小二乘拟合的大齿轮中心测量*
段振云,孟森森,赵文珍,赵文辉
(沈阳工业大学 机械工程学院,沈阳 110870)
0 引言
在工程上,一般将直径大于500mm的齿轮称为大齿轮[1]。大齿轮是大型机械装备中的重要零部件,其质量、性能及寿命直接影响设备的经济技术指标。现在大齿轮制造技术水平正在不断地提高,品种和规格也在不断的扩展,这对大齿轮测量技术以及测量仪器提出了更高的要求,从而促进了这一技术领域的发展[2]。
目前大齿轮测量主要依靠齿轮测量中心、三坐标测量机和激光跟踪齿轮在位测量系统等,用“以大测大”的方式来完成[3-4],但测量效率低且精度不高,限制了大齿轮制造水平的提高。在大齿轮齿廓的点位法测量中,确定大齿轮中心在测量坐标系中的位置是重要的测量基础。因此,国内外学者对大齿轮中心测量方法进行了大量研究[5],但现有的测量方法都较为复杂。本文针对上述问题,提出基于机器视觉在机测量大齿轮回转中心的方法。
1 定半径差测量方法
1.1 定半径差测量方法模型
将两个圆形贴片固定在如图1所示的贴片板上,经过精确测量得到两贴片中心点之间的距离L。如图2所示,贴片板固定在大齿轮上端面的径向方向上,两贴片中心点A和A′随着大齿轮旋转,形成半径差为R=R-R′的两个圆弧。Pi和Pi′为大齿轮旋转到第i个位置时两贴片中心点A与A′的位置,Pik和Pik′为第i+k个位置。
两圆弧上任意两个位置的弦长lik和lik′之比等于圆弧半径R和R′的比值。
图1 贴片板的图像

图2 定半径差测量方法模型
设所采集的采样点个数为n,贴片点A和A′的采样点坐标可记为:
其中,第i个与第i+k个采样点之间的弦长为:
(2)
设
则
(3)
aik应为常量,为了消除其随机误差,采用最小二乘法对aik进行统计计算,使
(4)
最小,则
由式(3)可得圆弧半径:
(5)
再利用半径约束的最小二乘圆心拟合方法可得到大齿轮的中心点坐标(x0,y0)。
1.2 半径差拟合模型的误差分析
影响定半径差最小二乘的拟合方法拟合精度的因素有弦长比值aik和半径差△R。
1.2.1 弦长比值aik对半径拟合误差的影响
在测量仪器精度一定的条件下,若弦长的最大误差为△l,则弦长误差导致的半径拟合误差ω1为:
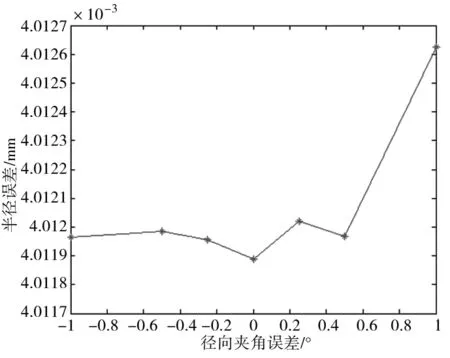
一般△l< (6) 从式(6)可以看出,当测量仪器精度一定时,弦长长度lik越大,半径拟合误差w1越小,但为了减小弦长比值aik的随机误差,所取弦长个数越多越好。在测量视野范围一定的情况下,弦长个数与弦长长度lik成负相关关系。因此,在保证足够精度的前提下,应选取较大的弦长长度lik。 1.2.2 半径差△R对半径拟合误差的影响 半径差△R的误差δ△R是由两贴片中心点之间的距离测量误差δL和两贴片中心点的径向夹角误差θ构成。如图3所示,△R的误差δr为: δ△R=δLcosθ+ΔR(1-cosθ) (7) 则由此产生的半径R拟合误差为: (8) 可得: (9) 该项误差主要受L的测量误差和固定贴片板时的方向误差的影响,随着距离测量误差δL和径向夹角误差θ的增大而增大。 式(8)还可以简化为: (10) 为了对上述分析进行验证,仿真一个半径为2000mm的大齿轮,取半径分别为1600mm和2000mm的圆,根据相机的拍照速度和大齿轮的旋转速度,取其中20°的圆弧,采集圆周上60个数据点作为采样数据,考虑一系列误差的影响加入±0.01mm的随机误差模拟实际测量数据。 分别取不同的弦长长度lik,即不同的k与n的比值,且只取相距k个采样点之间的弦长计算半径误差,实验结果如图4所示。 图4 k与n的比值对半径误差的影响 在上述条件下,取相距k及k以上的采样点之间的弦长计算半径误差,实验结果如图5所示。 图5 k与n的比值对半径误差的影响 由图4和图5看出,取相距k及k以上的采样点之间的弦长时精度较高,但不同的弦长长度对精度影响不大,考虑到会影响运算速度,因此在保证精度的同时,选择较大的k值,以便提高计算速度。 取不同数目的数据点,计算半径误差。实验结果如图6所示。 图6 数据点个数对半径误差的影响 从图6中看出,半径误差随着数据点个数的增加而减小,因此应适当的增加数据点个数。 半径差保持不变,取不同的半径值,计算半径误差,实验结果如图7所示。 图7 半径差与半径的比值对半径误差的影响 从图7看出,半径误差随着半径差与半径比值的增加而减小。因此,可以通过增加半径差的相对大小来提高圆心的拟合精度。 分别对半径差附加不同的距离测量误差,其实验结果如图8所示。 图8 距离测量误差对半径误差的影响 根据现有技术,两贴片中心点之间的径向夹角误差可控制在1°内,所以给两圆上的数据点加上±1°范围内的径向夹角误差,其结果如图9所示。 图9 径向夹角误差对半径误差的影响 从图8和图9看出,距离测量误差在半径差误差中占了主导作用,且半径差误差随之增加而增加。 由于半径差与半径的比值决定测量的精度,为验证该方法的可行性,用小圆盘进行实验验证,并推广到大齿轮上。其中拍摄图像的设备来源于文献[6]。用三坐标测量机对该标定圆盘上圆1与圆2、圆2与圆3之间的半径差进行测量,作为理论的半径差,圆1与圆2之间的半径差为8.010mm,圆2与圆3之间的半径差为7.992mm,如图10所示。 图10 实际圆盘图像 对所拍摄的30幅图中的圆1、圆2、圆3进行图像处理,得出各个圆在每幅图中的圆心位置,再利用三坐标测量机所测得的半径差,使用本文方法对其进行处理,以三坐标测量出的圆1半径104.982mm作为理论值,与无约束最小二乘拟合所得结果进行比较。半径差与半径的比值分别为0.08、0.15时,其结果如表1所示。 表1 所测圆心偏差量结果(单位:mm) 由表1看出,以三坐标测量机所测结果为理论值,半径差约束最小二乘拟合法所测误差小于0.11mm,其精度明显比最小二乘拟合法高;当定半径差与半径比值变大时,定半径差的最小二乘拟合法的精度达到0.0002mm,所以在实际的测量过程中,定半径差与半径比值的取值应尽量大,以此来提高测量的精度。 当大齿轮半径为2000mm,半径差为400mm时,齿轮中心位置误差为0.033mm,一般齿轮中心位置误差对齿廓总偏差的影响为其误差值的1/4[7],所以本文方法对大齿轮齿廓总偏差测量的影响为0.0083mm,5级精度大齿轮齿廓总偏差的允许值为0.025mm,所以本方法可用于大齿轮齿廓总偏差的测量。 本文提出半径差约束最小二乘圆拟合法测量大齿轮回转中心,并对各种影响因素进行理论分析及仿真实验,实验表明测量误差随着数据点个数、半径差与半径的比值的增加而减小;随着半径差误差的增加而增加,距离测量误差在半径差误差中占主导作用。本文以圆盘作为实验对象,结果表明半径差约束的最小二乘法拟合精度明显比无约束的最小二乘拟合法高,并且其测量结果接近于三坐标测量机的测量结果。本文方法对大齿轮齿廓总偏差测量的影响为0.0083mm,可用于大齿轮齿廓总偏差的测量。
2 圆心拟合精度的仿真分析
2.1 弦长长度lik的误差仿真分析
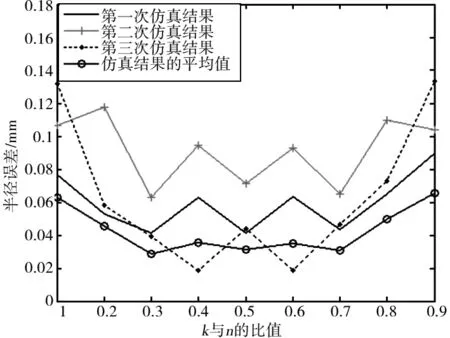
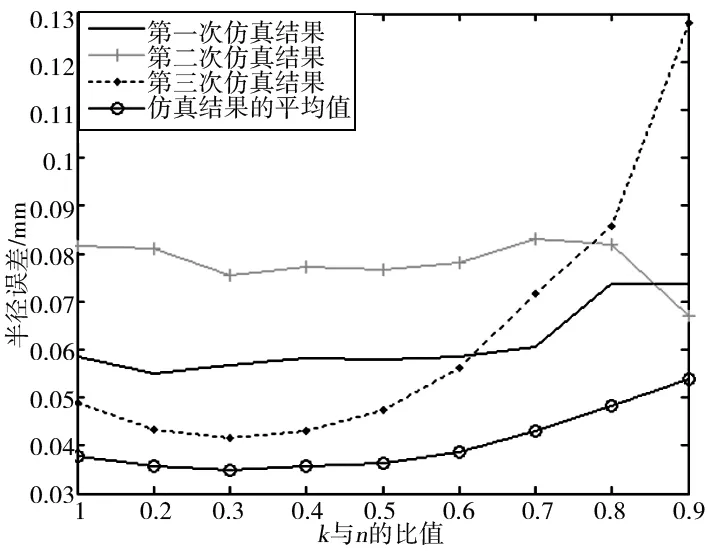
2.2 数据点个数的仿真分析

2.3 半径差与半径比值的仿真分析
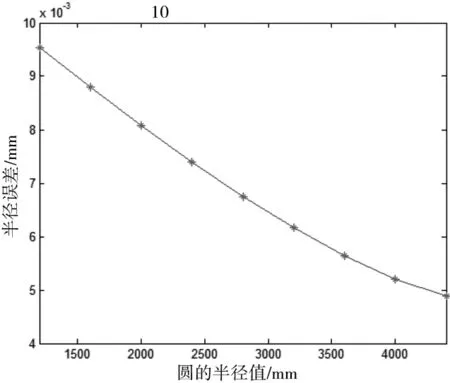
2.4 半径差误差的仿真分析

3 圆心拟合精度的实例分析


4 结论

