基于LTCA的高速齿轮传动系统非线性动态特性分析*

董 皓，刘志宇，方宗德,2

(1.西安工业大学 机电工程学院，西安 710021; 2.西北工业大学 机电学院，西安 710072)

0 引言

高速齿轮传动除具有更高的接触疲劳强度和弯曲疲劳强度外，还提出了传动平稳、噪声小和重量轻等需求。如何建立多种激励因素条件下的精确动力学模型，分析其动态特性，是亟需解决的问题。国内外学者在这方面开展了大量研究，Saghafi[1]进行了直齿圆柱齿轮系统混沌动力学控制的分析与研究；Fernandez-del- Rincon[2]提出了一种改进后的齿轮传动动力学模型；王峰[3]考虑了齿轮承载接触特性，分析了重合度对单对人字齿轮副非线性系统振动特性的影响；文献[4]研究了齿轮内部激励等参数对高速机车齿轮传动系统非线性特性的影响；文献[5]研究了齿面摩擦对齿轮传动系统分岔与混沌特性的影响；文献[6]建立了一种考虑齿侧间隙、齿面摩擦力和时变啮合刚度等因素的三齿轮扭转振动模型，研究了摩擦因素对模型动态特性的影响；文献[7]采用CPNF方法研究了传递功率对行星齿轮传动系统周期运动稳定性的局部精细分岔影响。还有一些学者[8-10]对齿轮传动系统的动态特性进行了研究。

本文针对高速齿轮传动系统的动力学问题展开研究，由轮齿接触分析以及轮齿承载接触分析计算出轮齿综合啮合刚度和单齿啮合刚度，考虑时变啮合刚度激励、当量啮合误差、齿面摩擦、齿侧间隙等激励因素的影响，建立高速齿轮传动系统的弯—扭耦合动态模型，研究各激励参数对齿轮非线性动态响应的影响，分析了载荷变化、啮合刚度、加工精度和弹性支撑刚度对动态特性的影响。为合理的高速齿轮传动系统动态特性分析与设计提供理论指导。

1 高速齿轮传动系统的振动模型

图1为高速齿轮传动系统的弯-扭耦合动力学模型[11]，T1、T2表示主、从动轮上作用的力矩；rb1、rb2表示主、从动轮的基圆半径；θ1、θ2表示主、从动轮的扭转角位移，以坐标点O1、O2为起始点；e12(t)表示主动轮与从动轮等效到啮合线上的当量啮合误差；km(t)、cm表示齿轮副的综合时变啮合刚度和啮合阻尼；kx1、ky1和kx2、ky2分别表示主动轮和被动轮上x、y方向的弹性支撑刚度；cx1、cy1和cx1、cy1分别表示主动轮和被动轮上x、y方向的弹性支撑阻尼。

图1 弯-扭耦合动力学模型

根据图1，该系统的横向-扭转振动位移阵列为：

(1)

其中，x1、y1表示主动轮1在x、y方向的微位移；x2、y2表示主动轮2在x、y方向的微位移。

定义该高速齿轮副的动态传递误差yd(t)为：

yd(t)=y2-y1-rb1θ1-rb2θ2

(2)

动态传递误差yd(t)与静态当量啮合误差e12(t)的差值为y(t)可以表示为：

y(t)=y2-y1-rb1θ1-rb2θ2-e12(t)

(3)

轮齿间的动态啮合力Fp可以表示为：

(4)

式中，f(y(t))为间隙非线性函数，可以表示为：

(5)

齿面摩擦力Ff可以近似表示为：Ff=λμFp，μ表示等效摩擦系数；λ表示齿轮摩擦力方向系数，当Ff沿x正方向时取“+1”，反之取为“-1”。

系统弯扭耦合的动力学分析模型可以表示为：

(6)

式中，S1、S2为啮合点相对于主、从动轮的摩擦力臂；J1、J2为主、从动轮的等效转动惯量。

将式(2)～式(6)代入式(7)中，并简化得：

(7)

m1和m2分别表示齿轮1和齿轮2的集中质量，单位kg。

此动力学微分方程中包含了时变啮合刚度、啮合冲击和时变支撑刚度等因素的影响。定义量纲一时间：τ=ωnt，ωn表示角速度，同时引进位移标称尺度bc，并令bc=b，对上述动力学模型进行量纲一化，采用数值积分法求解，得到系统的动态响应特性。

2 动力学模型的主要激励条件计算

2.1 时变啮合刚度激励计算

图2表示了齿轮副轮齿的承载分析模型[2]，图中接触曲线表示齿面在接触椭圆长轴方向的横截面，每一对齿上的i表示瞬时接触点(接触椭圆中心)，j表示沿长轴方向上的离散点，w表示接触前初始间距。轮齿变形前，两对接触的轮齿I和II的齿面初始间隙为：

[w]k=[δ]k+[b]k(k为I，II)

(8)

式中，[w]k=[w1k,w2k, …,wik,…,wjk,wnk]T，[b]k=[b1,b2, …,bi,…,bn]T，[δ]k=[1, 1, …, 1,…, 1]T，其中，n为瞬时接触椭圆长轴上离散点的个数，b为齿对k的齿面法向间隙，在瞬时接触椭圆中心bi=0，δ表示齿对k的几何传动误差，Z表示法向位移。

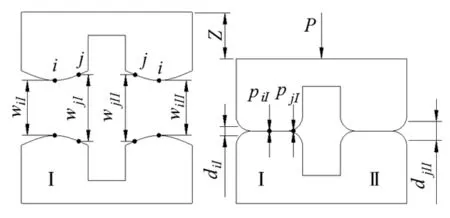
图2 承载接触分析模型

在载荷P作用下，轮齿发生弹性变形，弹性变形的变形协调条件为：

[F]k[p]k+[w]k=[Z]k+[d]k(k为I,II)

(9)

式中，[F]k是一对接触轮齿k的法向柔度矩阵; [p]k=[p1k,p2k, …,pik,…,pjk,pnk]T是一对接触轮齿k的接触椭圆长轴离散点j(j=1,2,…,n)处的法向载荷；[Z]k=[1, 1, …, 1,…, 1]T为轮齿在载荷作用下的法向位移；[d]k=[d1k,d2k, …,dik,…,djk,dnk]T是一对接触轮齿k的接触椭圆长轴离散点j处变形后的齿面间隙。

离散点的法向载荷pj(j=1,…,n)满足力学平衡关系：

(10)

由接触问题的非嵌入条件，满足pjk>0，则有djk=0，满足pjk=0，则有djk>0。

轮齿在外载荷P的作用下，产生的弹性变形引起的综合角变形误差Δφ主要由几何传动误差δ1、弯曲变形δ2和接触变形δ3三部分组成，则综合角变形Δφ和齿轮副传递扭矩T(k)的关系满足下式[12]：

(11)

式中，a，b，c为常数项，δ1=a，δ2=bT(k)，δ3=cT(k)2/3；T12(k)表示在一个啮合周期中被动轮对主齿轮在第k(k=1,…,5) 个啮合位置的扭矩。

齿轮副的时变啮合刚度km(k)可以按下式求解：

(12)

根据算例分析中的参数，计算时变啮合刚度激励如图3，且与石川法进行了对比，具有较好的一致性。

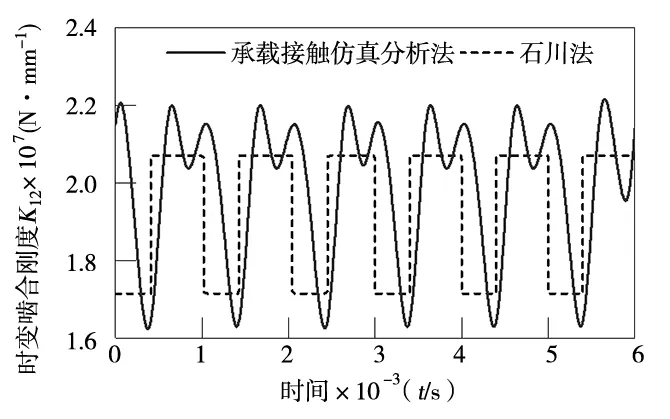
图3 时变啮合刚度激励条件

2.2 当量啮合误差激励条件计算

定义主动轮和从动轮的偏心误差Eep、Eeg与啮合线正向间的夹角ηEep、ηEeg分别为ηEep=-π/2+α+βEep+ωpt、ηEeg=-π/2+α+βEeg+ωgt，ωp、ωg为主动轮和从动轮的旋转角速度；βEep、βEeg为主、从动轮的偏心误差方位角。

主、从动轮的偏心误差Eep和Eeg当量啮合误差eEep和eEeg为：

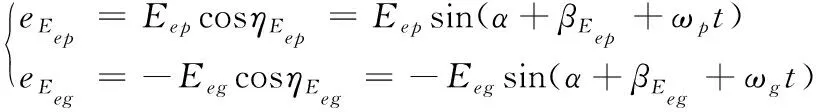
(13)

主、从动轮的基节误差Ebp和Ebg当量啮合误差eEbp和eEbg为：

(14)

主、从动轮的齿形误差Efp和Efg当量啮合误差eEfp和eEfg分别为：

(15)

主、从动轮的偏心误差的当量啮合误差的总和：

eEpg=eEep+eEbp+eEfp+eEeg-eEbg-eEfg

(16)

主、从动轮的安装误差Aep和Aeg当量啮合误差eAep和eAeg分别为：

(17)

式中，βAep、βAeg为主、从动轮的安装误差方位角。

主、从动轮的安装误差的当量啮合误差的总和eApg：

eApg=eAep+eAeg

(18)

主、从动轮的偏心误差和安装误差的当量啮合误差总和epg可以表示为：

epg=eEpg+eApg

(19)

3 算例分析

各齿轮的参数为：Z1=20，Z2=53，模数取2，压力角20°，变位系数x1=0.053，x2=-0.053，质量m1=1.5 kg，m2=4.5 kg，齿侧间隙取0.1 mm，负载扭矩132.5 N·m，给定系统输入功率200 kW，系统输入转速为15000 r/min，给定加工精度等级为5级。给定主动轮的偏心误差和安装误差分别为10μm和8μm，基节误差和齿形误差分别为5μm和4μm，从动轮的偏心误差和安装误差分别为12μm和11μm，基节误差和齿形误差分别为5.5μm和4.5μm。

计算得到转速在7000 r/min、10000 r/min和15000 r/min三种条件下的系统动态响应曲线如图4所示。

(a) 转速为7000r/min时系统的动态响应特性

(b) 转速为10000r/min时系统的动态响应特性

(c) 转速为15000r/min时系统的动态响应特性图4 不同转速条件下的系统动态响应特性

从图4可以看出，当系统转速为7000r/min时，时间历程非周期变化，相平面为具有一定宽度的曲线带，庞加莱截面上的点集近似地分布在一条曲线上，FFT频谱离散的分布在基频的整数倍点上，系统的运动为近似的拟1周期运动；当系统转速为10000 r/min时，时间历程非周期变化，相平面为具有一定宽度的曲线带，庞加莱截面上的点集近似地分布在两条曲线上，FFT频谱离散的分布在基频整数倍的1/2点上，系统的运动为近似的拟2周期运动；当系统转速为15000 r/min时，时间历程仍然非周期变化，相平面为互相缠绕和交叉但不重复不封闭的曲线，庞加莱截面由分布在一定区域上的不可数点集构成，FFT频谱是有界区域上具有一定宽度的连续谱，表明系统进入了混沌运动状态。

在系统的复杂激励的因素影响下，高速齿轮传动系统的动态响应并没有出现规范的周期运动状态，并且系统的运动状态非常复杂，经历了由近似的拟1周期运动分叉变化为近似的拟2周期运动，之后由近似的拟2周期运动进入混沌运动状态，具有很强的非线性性质。

系统载荷变化、啮合刚度、加工精度和弹性支撑刚度对动态特性的影响如图5所示。

(a) 载荷变化 (b) 啮合刚度变化

(c) 加工精度变化 (d) 弹性支撑刚度变化图5 各因素对系统幅频响应特性的影响

由图5可以看出，载荷逐渐从轻载到重载变化时，系统的振动频率带逐渐增多，主谐波与其余各阶谐波的响应幅值也在不断的加大；随着齿轮啮合刚度的提高，传动系统的共振动频率带不断减少，运动特性逐渐由混沌运动转向拟周期运动，主谐波的响应幅值也在不断地降低，提高齿轮副的啮合刚度从一定程度上可降低系统的振动；齿轮的精度对高速齿轮传动系统的响应幅值的影响比较显著，随着齿轮精度等级的降低，传动系统的共振频率带逐渐增多，而且各阶谐波响应的幅值也在不断地增大；随着等效支撑刚度的增加，系统的幅频响应特性基本没有发生变化，系统也一直处于复杂的混沌运动状态，系统主谐波的响应幅值变动没有表现出一定的规律性，但从整体的变动量来看非常微小。

4 结论

本文建立了高速齿轮传动系统的弯—扭耦合动态模型，分析了转速、载荷变化、啮合刚度、加工精度和弹性支撑刚度对动态特性的影响，所得结论如下：

(1) 基于承载接触仿真分析方法，能够获得符合实际工况下的时变啮合刚度激励条件，更真实的反映系统各齿轮副每个啮合位置下的动态响应特性；

(2) 转速从7000r/min变化到15000r/min时，时间历程一直表现为非周期变化，系统经历了从拟1周期运动、拟2周期运动到混沌状态的变化，具有很强的非线性性质；

(3) 适当增大轮齿啮合刚度和提高齿轮副精度等级可改善系统的动力学性能，在系统支撑刚度足够的条件下，不断的增大支撑刚度并不会改善系统的振动特性。